Virial theorem
Encyclopedia
In mechanics
, the virial theorem provides a general equation relating the average over time of the total kinetic energy
,
, of a stable system consisting of N particles, bound by potential forces, with that of the total potential energy, 
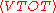, where angle brackets represent the average over time of the enclosed quantity. Mathematically, the theorem
states
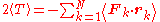
where Fk represents the force
on the kth particle, which is located at position rk. The word "virial" derives from vis, the Latin
word for "force" or "energy", and was given its technical definition by Clausius in 1870.
The significance of the virial theorem is that it allows the average total kinetic energy to be calculated even for very complicated systems that defy an exact solution, such as those considered in statistical mechanics
; this average total kinetic energy is related to the temperature
of the system by the equipartition theorem
. However, the virial theorem does not depend on the notion of temperature
and holds even for systems that are not in thermal equilibrium
. The virial theorem has been generalized in various ways, most notably to a tensor
form.
If the force between any two particles of the system results from a potential energy
V(r) = αr n that is proportional to some power n of the inter-particle distance
r, the virial theorem adopts a simple form
Thus, twice the average total kinetic energy
equals n times the average total potential energy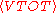 
. Whereas V(r) represents the potential energy between two particles, VTOT represents the total potential energy of the system, i.e., the sum of the potential energy V(r) over all pairs of particles in the system. A common example of such a system is a star held together by its own gravity, where n equals −1.
Although the virial theorem depends on averaging the total kinetic and potential energies, the presentation here postpones the averaging to the last step.
delivered the lecture "On a Mechanical Theorem Applicable to Heat" to the Association for Natural and Medical Sciences of the Lower Rhine, following a 20 year study of thermodynamics. The lecture stated that the mean vis viva of the system is equal to its virial, or that the average kinetic energy is equal to 1/2 the average potential energy. The virial theorem can be obtained directly from Lagrange's
Identity as applied in classical gravitational dynamics, the original form of which was included in his "Essay on the Problem of Three Bodies" published in 1772. Karl Jacobi's generalization of the identity to n bodies and to the present form of Laplace's identity closely resembles the classical virial theorem. However, the interpretations leading to the development of the equations were very different, since at the time of development, statistical dynamics had not yet unified the separate studies of thermodynamics and classical dynamics. The theorem was later utilized, popularized, generalized and further developed by persons such as James Clerk Maxwell
, Lord Rayleigh
, Henri Poincaré
, Subrahmanyan Chandrasekhar
, Enrico Fermi
, Paul Ledoux
and Eugene Parker
. Fritz Zwicky
was the first to use the virial theorem to deduce the existence of unseen matter, which is now called dark matter
. As another example of its many applications, the virial theorem has been used to derive the Chandrasekhar limit
for the stability of white dwarf
star
s.
moment of inertia
I about the origin
is defined by the equation
where mk and rk represent the mass and position of the kth particle. rk=|rk| is the position vector magnitude. The scalar virial G is defined by the equation
where pk is the momentum
vector of the kth particle. Assuming that the masses are constant, the virial G is one-half the time derivative of this moment of inertia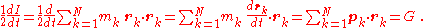
In turn, the time derivative of the virial G can be written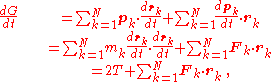
where mk is the mass of the k-th particle,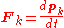
is the net force on that particle, and T is the total kinetic energy
of the system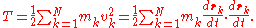
on particle k is the sum of all the forces from the other particles j in the system
where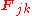
is the force applied by particle j on particle k. Hence, the force term of the virial time derivative can be written
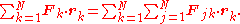
Since no particle acts on itself (i.e.,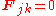
whenever 
), we have
where we have assumed that Newton's third law of motion
holds, i.e.,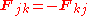
(equal and opposite reaction).
It often happens that the forces can be derived from a potential energy V that is a function only of the distance rjk between the point particles j and k. Since the force is the negative gradient of the potential energy, we have in this case
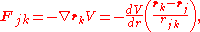
which is clearly equal and opposite to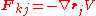
, the force applied by particle 
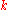on particle j, as may be confirmed by explicit calculation. Hence, the force term of the virial time derivative is
Thus, we have
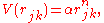
where the coefficient α and the exponent n are constants. In such cases, the force term of the virial time derivative is given by the equation
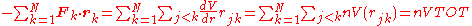
where VTOT is the total potential energy of the system
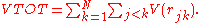
Thus, we have
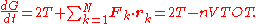
For gravitating systems and also for electrostatic systems
, the exponent n equals −1, giving Lagrange's identity
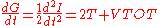
which was derived by Lagrange and extended by Jacobi.
is defined as
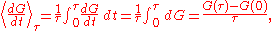
from which we obtain the exact equation
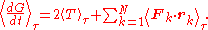
The virial theorem states that, if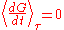
, then
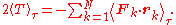
There are many reasons why the average of the time derivative might vanish, i.e.,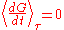
. One often-cited reason applies to stable bound systems, i.e., systems that hang together forever and whose parameters are finite. In that case, velocities and coordinates of the particles of the system have upper and lower limits so that the virial 
is bounded between two extremes, 
and 
, and the average goes to zero in the limit of very long times 
Even if the average of the time derivative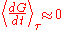
is only approximately zero, the virial theorem holds to the same degree of approximation.
For power-law forces with an exponent n, the general equation holds
For gravitational attraction
, n equals −1 and the average kinetic energy equals half of the average negative potential energy
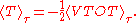
This general result is useful for complex gravitating systems such as solar system
s or galaxies
.
A simple application of the virial theorem concerns galaxy clusters. If a region of space is unusually full of galaxies, it is safe to assume that they have been together for a long time, and the virial theorem can be applied. Doppler measurements give lower bounds for their relative velocities, and the virial theorem gives a lower bound for the total mass of the cluster, including any dark matter.
The averaging need not be taken over time; an ensemble average
can also be taken, with equivalent results.
Although derived for classical mechanics, the virial theorem also holds for quantum mechanics, which was proved by Fock (the quantum equivalent of the l.h.s.
vanishes for energy eigenstates).
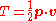. Instead, it is true that 
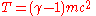and
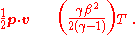
The last expression can be simplified to eithe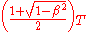r
or 
.
Thus, under the conditions described in earlier sections (including Newton's third law of motion,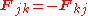
, despite relativity), the time average for 
particles with a power law potential is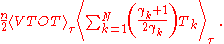
In particular, the ratio of kinetic energy to potential energy is no longer fixed, but necessarily falls into an interval: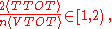
where the more relativistic systems exhibit the larger ratios.
applied a form of the virial theorem in 1911 to the problem of determining cosmological stability. A variational form of the virial theorem was developed in 1945 by Ledoux. A tensor
form of the virial theorem was developed by Parker, Chandrasekhar and Fermi. The following generalization of the virial theorem has been established by Pollard in 1964 for the case of the inverse square law
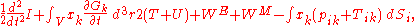
where I is the moment of inertia
, G is the momentum density of the electromagnetic field
, T is the kinetic energy
of the "fluid", U is the random "thermal" energy of the particles, WE and WM are the electric and magnetic energy content of the volume considered. Finally, pik is the fluid-pressure tensor expressed in the local moving coordinate system
and Tik is the electromagnetic stress tensor,
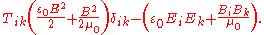
A plasmoid
is a finite configuration of magnetic fields and plasma. With the virial theorem it is easy to see that any such configuration will expand if not contained by external forces. In a finite configuration without pressure-bearing walls or magnetic coils, the surface integral will vanish. Since all the other terms on the right hand side are positive, the acceleration of the moment of inertia will also be positive. It is also easy to estimate the expansion time τ. If a total mass M is confined within a radius R, then the moment of inertia is roughly MR2, and the left hand side of the virial theorem is MR2/τ2. The terms on the right hand side add up to about pR3, where p is the larger of the plasma pressure or the magnetic pressure. Equating these two terms and solving for τ, we find
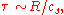
where cs is the speed of the ion acoustic wave
(or the Alfvén wave
, if the magnetic pressure is higher than the plasma pressure). Thus the lifetime of a plasmoid is expected to be on the order of the acoustic (or Alfvén) transit time.
, the term virial radius is used to refer to the radius of a sphere, centered on a galaxy
or a galaxy cluster
, within which virial equilibrium holds. Since this radius is difficult to determine observationally, it is often approximated as the radius within which the average density is greater, by a specified factor, than the critical density
. (Here, H is the Hubble parameter
and G is the gravitational constant
.) A common choice for the factor is 200, in which case the virial radius is approximated as r200.
Mechanics
Mechanics is the branch of physics concerned with the behavior of physical bodies when subjected to forces or displacements, and the subsequent effects of the bodies on their environment....
, the virial theorem provides a general equation relating the average over time of the total kinetic energy
Kinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
,
, of a stable system consisting of N particles, bound by potential forces, with that of the total potential energy, 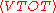, where angle brackets represent the average over time of the enclosed quantity. Mathematically, the theoremTheorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
states
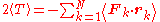
where Fk represents the force
Force
In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
on the kth particle, which is located at position rk. The word "virial" derives from vis, the Latin
Latin
Latin is an Italic language originally spoken in Latium and Ancient Rome. It, along with most European languages, is a descendant of the ancient Proto-Indo-European language. Although it is considered a dead language, a number of scholars and members of the Christian clergy speak it fluently, and...
word for "force" or "energy", and was given its technical definition by Clausius in 1870.
The significance of the virial theorem is that it allows the average total kinetic energy to be calculated even for very complicated systems that defy an exact solution, such as those considered in statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
; this average total kinetic energy is related to the temperature
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
of the system by the equipartition theorem
Equipartition theorem
In classical statistical mechanics, the equipartition theorem is a general formula that relates the temperature of a system with its average energies. The equipartition theorem is also known as the law of equipartition, equipartition of energy, or simply equipartition...
. However, the virial theorem does not depend on the notion of temperature
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
and holds even for systems that are not in thermal equilibrium
Thermal equilibrium
Thermal equilibrium is a theoretical physical concept, used especially in theoretical texts, that means that all temperatures of interest are unchanging in time and uniform in space...
. The virial theorem has been generalized in various ways, most notably to a tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
form.
If the force between any two particles of the system results from a potential energy
Potential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
V(r) = αr n that is proportional to some power n of the inter-particle distance
Mean inter-particle distance
Mean inter-particle distance is the mean distance between microscopic particles in a macroscopic body.-Ambiguity:...
r, the virial theorem adopts a simple form
Thus, twice the average total kinetic energy
equals n times the average total potential energy 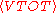. Whereas V(r) represents the potential energy between two particles, VTOT represents the total potential energy of the system, i.e., the sum of the potential energy V(r) over all pairs of particles in the system. A common example of such a system is a star held together by its own gravity, where n equals −1.Although the virial theorem depends on averaging the total kinetic and potential energies, the presentation here postpones the averaging to the last step.
History of the virial theorem
In 1870, Rudolf ClausiusRudolf Clausius
Rudolf Julius Emanuel Clausius , was a German physicist and mathematician and is considered one of the central founders of the science of thermodynamics. By his restatement of Sadi Carnot's principle known as the Carnot cycle, he put the theory of heat on a truer and sounder basis...
delivered the lecture "On a Mechanical Theorem Applicable to Heat" to the Association for Natural and Medical Sciences of the Lower Rhine, following a 20 year study of thermodynamics. The lecture stated that the mean vis viva of the system is equal to its virial, or that the average kinetic energy is equal to 1/2 the average potential energy. The virial theorem can be obtained directly from Lagrange's
Joseph Louis Lagrange
Joseph-Louis Lagrange , born Giuseppe Lodovico Lagrangia, was a mathematician and astronomer, who was born in Turin, Piedmont, lived part of his life in Prussia and part in France, making significant contributions to all fields of analysis, to number theory, and to classical and celestial mechanics...
Identity as applied in classical gravitational dynamics, the original form of which was included in his "Essay on the Problem of Three Bodies" published in 1772. Karl Jacobi's generalization of the identity to n bodies and to the present form of Laplace's identity closely resembles the classical virial theorem. However, the interpretations leading to the development of the equations were very different, since at the time of development, statistical dynamics had not yet unified the separate studies of thermodynamics and classical dynamics. The theorem was later utilized, popularized, generalized and further developed by persons such as James Clerk Maxwell
James Clerk Maxwell
James Clerk Maxwell of Glenlair was a Scottish physicist and mathematician. His most prominent achievement was formulating classical electromagnetic theory. This united all previously unrelated observations, experiments and equations of electricity, magnetism and optics into a consistent theory...
, Lord Rayleigh
John Strutt, 3rd Baron Rayleigh
John William Strutt, 3rd Baron Rayleigh, OM was an English physicist who, with William Ramsay, discovered the element argon, an achievement for which he earned the Nobel Prize for Physics in 1904...
, Henri Poincaré
Henri Poincaré
Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
, Subrahmanyan Chandrasekhar
Subrahmanyan Chandrasekhar
Subrahmanyan Chandrasekhar, FRS ) was an Indian origin American astrophysicist who, with William A. Fowler, won the 1983 Nobel Prize for Physics for key discoveries that led to the currently accepted theory on the later evolutionary stages of massive stars...
, Enrico Fermi
Enrico Fermi
Enrico Fermi was an Italian-born, naturalized American physicist particularly known for his work on the development of the first nuclear reactor, Chicago Pile-1, and for his contributions to the development of quantum theory, nuclear and particle physics, and statistical mechanics...
, Paul Ledoux
Paul Ledoux
Paul Ledoux was a Belgian astronomer. In 1964 Paul Ledoux was awarded the Francqui Prize for Exact Sciences. He was awarded the Eddington Medal of the Royal Astronomical Society in 1972 for investigations into problems of stellar stability and variable stars...
and Eugene Parker
Eugene Parker
Eugene N. Parker is an American solar astrophysicist who received his B.S. degree in physics from Michigan State University in 1948 and Ph.D. from Caltech in 1951. In the mid 1950s Parker developed the theory on the supersonic solar wind and predicted the Parker spiral shape of the solar magnetic...
. Fritz Zwicky
Fritz Zwicky
Fritz Zwicky was a Swiss astronomer. He worked most of his life at the California Institute of Technology in the United States of America, where he made many important contributions in theoretical and observational astronomy.- Biography :Fritz Zwicky was born in Varna, Bulgaria to a Swiss father....
was the first to use the virial theorem to deduce the existence of unseen matter, which is now called dark matter
Dark matter
In astronomy and cosmology, dark matter is matter that neither emits nor scatters light or other electromagnetic radiation, and so cannot be directly detected via optical or radio astronomy...
. As another example of its many applications, the virial theorem has been used to derive the Chandrasekhar limit
Chandrasekhar limit
When a star starts running out of fuel, it usually cools off and collapses into one of three compact forms, depending on its total mass:* a White Dwarf, a big lump of Carbon and Oxygen atoms, almost like one huge molecule...
for the stability of white dwarf
White dwarf
A white dwarf, also called a degenerate dwarf, is a small star composed mostly of electron-degenerate matter. They are very dense; a white dwarf's mass is comparable to that of the Sun and its volume is comparable to that of the Earth. Its faint luminosity comes from the emission of stored...
star
Star
A star is a massive, luminous sphere of plasma held together by gravity. At the end of its lifetime, a star can also contain a proportion of degenerate matter. The nearest star to Earth is the Sun, which is the source of most of the energy on Earth...
s.
Definitions of the virial and its time derivative
For a collection of N point particles, the scalarScalar (physics)
In physics, a scalar is a simple physical quantity that is not changed by coordinate system rotations or translations , or by Lorentz transformations or space-time translations . This is in contrast to a vector...
moment of inertia
Moment of inertia
In classical mechanics, moment of inertia, also called mass moment of inertia, rotational inertia, polar moment of inertia of mass, or the angular mass, is a measure of an object's resistance to changes to its rotation. It is the inertia of a rotating body with respect to its rotation...
I about the origin
Origin (mathematics)
In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...
is defined by the equation
where mk and rk represent the mass and position of the kth particle. rk=|rk| is the position vector magnitude. The scalar virial G is defined by the equation
where pk is the momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
vector of the kth particle. Assuming that the masses are constant, the virial G is one-half the time derivative of this moment of inertia
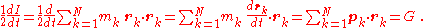
In turn, the time derivative of the virial G can be written
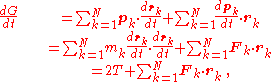
where mk is the mass of the k-th particle,
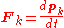is the net force on that particle, and T is the total kinetic energyKinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
of the system
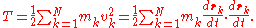
Connection with the potential energy between particles
The total force on particle k is the sum of all the forces from the other particles j in the systemwhere
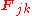is the force applied by particle j on particle k. Hence, the force term of the virial time derivative can be written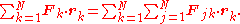Since no particle acts on itself (i.e.,
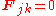whenever ), we havewhere we have assumed that Newton's third law of motion
Newton's laws of motion
Newton's laws of motion are three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motion due to those forces...
holds, i.e.,
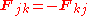(equal and opposite reaction).It often happens that the forces can be derived from a potential energy V that is a function only of the distance rjk between the point particles j and k. Since the force is the negative gradient of the potential energy, we have in this case
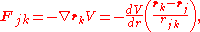
which is clearly equal and opposite to
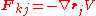, the force applied by particle 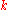on particle j, as may be confirmed by explicit calculation. Hence, the force term of the virial time derivative isThus, we have
Special case of power-law forces
In a common special case, the potential energy V between two particles is proportional to a power n of their distance r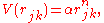where the coefficient α and the exponent n are constants. In such cases, the force term of the virial time derivative is given by the equation
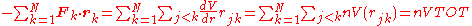
where VTOT is the total potential energy of the system
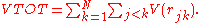
Thus, we have
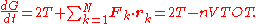
For gravitating systems and also for electrostatic systems
Electrostatics
Electrostatics is the branch of physics that deals with the phenomena and properties of stationary or slow-moving electric charges....
, the exponent n equals −1, giving Lagrange's identity
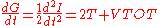
which was derived by Lagrange and extended by Jacobi.
Time averaging and the virial theorem
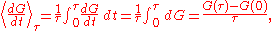
The average of this derivative over a time is defined asfrom which we obtain the exact equation
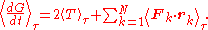
The virial theorem states that, if
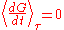, then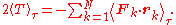There are many reasons why the average of the time derivative might vanish, i.e.,
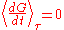. One often-cited reason applies to stable bound systems, i.e., systems that hang together forever and whose parameters are finite. In that case, velocities and coordinates of the particles of the system have upper and lower limits so that the virial is bounded between two extremes, and , and the average goes to zero in the limit of very long times Even if the average of the time derivative
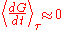is only approximately zero, the virial theorem holds to the same degree of approximation.For power-law forces with an exponent n, the general equation holds
For gravitational attraction
Gravitation
Gravitation, or gravity, is a natural phenomenon by which physical bodies attract with a force proportional to their mass. Gravitation is most familiar as the agent that gives weight to objects with mass and causes them to fall to the ground when dropped...
, n equals −1 and the average kinetic energy equals half of the average negative potential energy
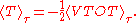
This general result is useful for complex gravitating systems such as solar system
Solar System
The Solar System consists of the Sun and the astronomical objects gravitationally bound in orbit around it, all of which formed from the collapse of a giant molecular cloud approximately 4.6 billion years ago. The vast majority of the system's mass is in the Sun...
s or galaxies
Galaxy
A galaxy is a massive, gravitationally bound system that consists of stars and stellar remnants, an interstellar medium of gas and dust, and an important but poorly understood component tentatively dubbed dark matter. The word galaxy is derived from the Greek galaxias , literally "milky", a...
.
A simple application of the virial theorem concerns galaxy clusters. If a region of space is unusually full of galaxies, it is safe to assume that they have been together for a long time, and the virial theorem can be applied. Doppler measurements give lower bounds for their relative velocities, and the virial theorem gives a lower bound for the total mass of the cluster, including any dark matter.
The averaging need not be taken over time; an ensemble average
Ensemble average
In statistical mechanics, the ensemble average is defined as the mean of a quantity that is a function of the micro-state of a system , according to the distribution of the system on its micro-states in this ensemble....
can also be taken, with equivalent results.
Although derived for classical mechanics, the virial theorem also holds for quantum mechanics, which was proved by Fock (the quantum equivalent of the l.h.s.
vanishes for energy eigenstates).The virial theorem and special relativity
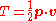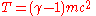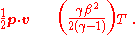
For a single particle in special relativity, it is not the case that. Instead, it is true that andThe last expression can be simplified to either
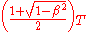or .Thus, under the conditions described in earlier sections (including Newton's third law of motion,
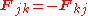, despite relativity), the time average for particles with a power law potential is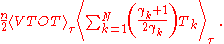In particular, the ratio of kinetic energy to potential energy is no longer fixed, but necessarily falls into an interval:
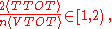
where the more relativistic systems exhibit the larger ratios.
Generalizations of the virial theorem
Lord Rayleigh published a generalization of the virial theorem in 1903. Henri PoincaréHenri Poincaré
Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
applied a form of the virial theorem in 1911 to the problem of determining cosmological stability. A variational form of the virial theorem was developed in 1945 by Ledoux. A tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
form of the virial theorem was developed by Parker, Chandrasekhar and Fermi. The following generalization of the virial theorem has been established by Pollard in 1964 for the case of the inverse square law
- the statement
is true if and only if 
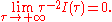A boundary term otherwise must be added, such as in Ref.
Inclusion of electromagnetic fields
The virial theorem can be extended to include electric and magnetic fields. The result is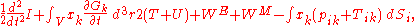where I is the moment of inertia
Moment of inertia
In classical mechanics, moment of inertia, also called mass moment of inertia, rotational inertia, polar moment of inertia of mass, or the angular mass, is a measure of an object's resistance to changes to its rotation. It is the inertia of a rotating body with respect to its rotation...
, G is the momentum density of the electromagnetic field
Poynting vector
In physics, the Poynting vector can be thought of as representing the directional energy flux density of an electromagnetic field. It is named after its inventor John Henry Poynting. Oliver Heaviside and Nikolay Umov independently co-invented the Poynting vector...
, T is the kinetic energy
Kinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
of the "fluid", U is the random "thermal" energy of the particles, WE and WM are the electric and magnetic energy content of the volume considered. Finally, pik is the fluid-pressure tensor expressed in the local moving coordinate system
and Tik is the electromagnetic stress tensor,
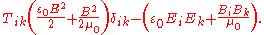
A plasmoid
Plasmoid
A plasmoid is a coherent structure of plasma and magnetic fields. Plasmoids have been proposed to explain natural phenomena such as ball lightning, magnetic bubbles in the magnetosphere, and objects in cometary tails, in the solar wind, in the solar atmosphere, and in the heliospheric current sheet...
is a finite configuration of magnetic fields and plasma. With the virial theorem it is easy to see that any such configuration will expand if not contained by external forces. In a finite configuration without pressure-bearing walls or magnetic coils, the surface integral will vanish. Since all the other terms on the right hand side are positive, the acceleration of the moment of inertia will also be positive. It is also easy to estimate the expansion time τ. If a total mass M is confined within a radius R, then the moment of inertia is roughly MR2, and the left hand side of the virial theorem is MR2/τ2. The terms on the right hand side add up to about pR3, where p is the larger of the plasma pressure or the magnetic pressure. Equating these two terms and solving for τ, we find
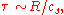
where cs is the speed of the ion acoustic wave
Ion acoustic wave
An ion acoustic wave is one type of longitudinal oscillation of the ions and electrons in a plasma, much like acoustic waves traveling in neutral gas. However, because the waves propagate through positively charged ions, ion acoustic waves can interact with their electromagnetic fields, as well as...
(or the Alfvén wave
Alfvén wave
An Alfvén wave, named after Hannes Alfvén, is a type of magnetohydrodynamic wave.-Definition:An Alfvén wave in a plasma is a low-frequency travelling oscillation of the ions and the magnetic field...
, if the magnetic pressure is higher than the plasma pressure). Thus the lifetime of a plasmoid is expected to be on the order of the acoustic (or Alfvén) transit time.
Virial radius
In astronomyAstronomy
Astronomy is a natural science that deals with the study of celestial objects and phenomena that originate outside the atmosphere of Earth...
, the term virial radius is used to refer to the radius of a sphere, centered on a galaxy
Galaxy
A galaxy is a massive, gravitationally bound system that consists of stars and stellar remnants, an interstellar medium of gas and dust, and an important but poorly understood component tentatively dubbed dark matter. The word galaxy is derived from the Greek galaxias , literally "milky", a...
or a galaxy cluster
Galaxy cluster
A galaxy cluster is a compact cluster of galaxies. Basic difference between a galaxy group and a galaxy cluster is that there are many more galaxies in a cluster than in a group. Also, galaxies in a cluster are more compact and have higher velocity dispersion. One of the key features of cluster is...
, within which virial equilibrium holds. Since this radius is difficult to determine observationally, it is often approximated as the radius within which the average density is greater, by a specified factor, than the critical density
. (Here, H is the Hubble parameterHubble's law
Hubble's law is the name for the astronomical observation in physical cosmology that: all objects observed in deep space are found to have a doppler shift observable relative velocity to Earth, and to each other; and that this doppler-shift-measured velocity, of various galaxies receding from...
and G is the gravitational constant
Gravitational constant
The gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...
.) A common choice for the factor is 200, in which case the virial radius is approximated as r200.
External links
- The Virial Theorem at MathPages
- Gravitational Contraction and Star Formation, Georgia State University