Ideal gas
Encyclopedia
An ideal gas is a theoretical gas
composed of a set of randomly-moving, non-interacting point particle
s. The ideal gas concept is useful because it obeys the ideal gas law
, a simplified equation of state
, and is amenable to analysis under statistical mechanics
.
At normal conditions such as standard temperature and pressure, most real gas
es behave qualitatively like an ideal gas. Many gases such as air, nitrogen
, oxygen
, hydrogen
, noble gases, and some heavier gases like carbon dioxide
can be treated like ideal gases within reasonable tolerances. Generally, a gas behaves more like an ideal gas at higher temperature
and lower density
(i.e. lower pressure
), as the work performed by intermolecular forces becomes less significant compared with the particles' kinetic energy
, and the size of the molecules becomes less significant compared to the empty space between them.
The ideal gas model tends to fail at lower temperatures or higher pressures, when intermolecular forces and molecular size become important. It also fails for most heavy gases, such as water vapor
or many refrigerant
s. At some point of low temperature and high pressure, real gases undergo a phase transition
, such as to a liquid
or a solid
. The model of an ideal gas, however, does not describe or allow phase transitions. These must be modeled by more complex equations of state
.
The ideal gas model has been explored in both the Newtonian dynamics
(as in "kinetic theory
") and in quantum mechanics
(as a "gas in a box
"). The ideal gas model has also been used to model the behavior of electrons in a metal (in the Drude model
and the free electron model
), and it is one of the most important models in statistical mechanics
.
The classical ideal gas can be separated into two types: The classical thermodynamic ideal gas and the ideal quantum Boltzmann gas. Both are essentially the same, except that the classical thermodynamic ideal gas is based on classical statistical mechanics
, and certain thermodynamic parameters such as the entropy
are only specified to within an undetermined additive constant. The ideal quantum Boltzmann gas overcomes this limitation by taking the limit of the quantum Bose gas and quantum Fermi gas in the limit of high temperature to specify these additive constants. The behavior of a quantum Boltzmann gas is the same as that of a classical ideal gas except for the specification of these constants. The results of the quantum Boltzmann gas are used in a number of cases including the Sackur-Tetrode equation
for the entropy of an ideal gas and the Saha ionization equation
for a weakly ionized plasma
.
The equation of state
of a classical ideal gas is the ideal gas law
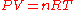
and the internal energy
of an ideal gas given by:
where
The amount of gas in J
·K
−1 is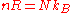
where
The probability distribution of particles by velocity or energy is given by the Boltzmann distribution
.
The ideal gas law is an extension of experimentally discovered gas laws
. Real fluids at low density
and high temperature
approximate the behavior of a classical ideal gas. However, at lower temperatures or a higher density
, a real fluid deviates strongly from the behavior of an ideal gas, particularly as it condenses from a gas into a liquid or solid. The deviation is expressed as a compressibility factor
.
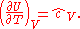
This is the dimensionless heat capacity at constant volume, which is generally a function of temperature due to intermolecular forces. For moderate temperatures, the constant for a monoatomic gas is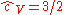
while for a diatomic gas it is 
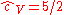. It is seen that macroscopic measurements on heat capacity provide information on the microscopic structure of the molecules.
The heat capacity at constant pressure of 1 J·K−1 ideal gas is:
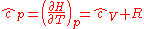
where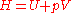
is the enthalpy
of the gas.
Sometimes, a distinction is made between an ideal gas, where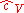
and 
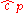could vary with pressure and temperature, and a perfect gas
, for which this is not the case.
only, we can go a long way in determining the expression for the entropy
of an ideal gas. This is an important step since, according to the theory of thermodynamic potentials, if we can express the entropy as a function of U (U is a thermodynamic potential) and the volume V, then we will have a complete statement of the thermodynamic behavior of the ideal gas. We will be able to derive both the ideal gas law and the expression for internal energy from it.
Since the entropy is an exact differential
, using the chain rule
, the change in entropy when going from a reference state 0 to some other state with entropy S may be written as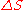
where:
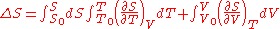
where the reference variables may be functions of the number of particles N. Using the definition of the heat capacity
at constant volume for the first differential and the appropriate Maxwell relation for the second we have:
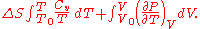
Expressing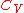
in terms of 
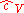as developed in the above section, differentiating the ideal gas equation of state, and integrating yields:
where all constants have been incorporated into the logarithm as f(N) which is some function of the particle number N having the same dimensions as
in order that the argument of the logarithm be dimensionless. We now impose the constraint that the entropy be extensive. This will mean that when the extensive parameters (V and N) are multiplied by a constant, the entropy will be multiplied by the same constant. Mathematically:
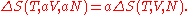
From this we find an equation for the function f(N)
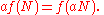
Differentiating this with respect to a, setting a equal to unity, and then solving the differential equation yields f(N):
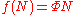
where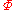
is some constant with the dimensions of 
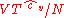. Substituting into the equation for the change in entropy:
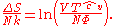
This is about as far as we can go using thermodynamics alone. Note that the above equation is flawed — as the temperature approaches zero, the entropy approaches negative infinity, in contradiction to the third law of thermodynamics
. In the above "ideal" development, there is a critical point, not at absolute zero, at which the argument of the logarithm becomes unity, and the entropy becomes zero. This is unphysical. The above equation is a good approximation only when the argument of the logarithm is much larger than unity — the concept of an ideal gas breaks down at low values of V/N. Nevertheless, there will be a "best" value of the constant in the sense that the predicted entropy is as close as possible to the actual entropy, given the flawed assumption of ideality. It remained for quantum mechanics
to introduce a reasonable value for the value of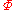
which yields the Sackur-Tetrode equation
for the entropy of an ideal gas. It too suffers from a divergent entropy at absolute zero, but is a good approximation to an ideal gas over a large range of densities.
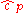is a constant we can express the entropy in what will prove to be a more convenient form:
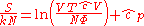
where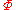
is now the undetermined constant. The chemical potential
of the ideal gas is calculated from the corresponding equation of state (see thermodynamic potential):
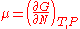
where G is the Gibbs free energy
and is equal to
so that:
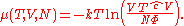
The thermodynamic potentials for an ideal gas can now be written as functions of T, V, and N as:
The most informative way of writing the potentials is in terms of their natural variables, since each of these equations can be used to derive all of the other thermodynamic variables of the system. In terms of their natural variables, the thermodynamic potentials of a single-species ideal gas are:
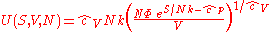
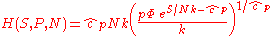
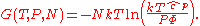
In statistical mechanics
,
the relationship between the Helmholtz free energy
and the
partition function
is fundamental, and is used to calculate the
thermodynamic properties
of matters; see
configuration integral
for more details.
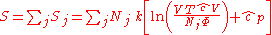
where the sum is over all species. Likewise, the free energies are equal to the sums of the free energies of each species so that if Φ is a thermodynamic potential then
where Φj is expressed in terms of its natural variables. For example, the internal energy will be
where N is defined as
Ideal gasses are not found in the real world. So they are different from real gasses. There are basic assumptions made in the kinetic theory of gasses.
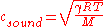
where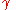
is the adiabatic index
is the universal gas constant
is the temperature
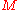is the molar mass
of the gas.
theory itself predicts the same thing. Any gas behaves as an ideal gas at high enough temperature and low enough density, but at the point where the Sackur-Tetrode equation
begins to break down, the gas will begin to behave as a quantum gas, composed of either bosons or fermions. (See the gas in a box
article for a derivation of the ideal quantum gases, including the ideal Boltzmann gas.)
Gases tend to behave as an ideal gas over a wider range of pressures when the temperature reaches the Boyle temperature.
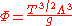
where Λ is the thermal de Broglie wavelength of the gas and g is the degeneracy
of states.
(e.g. a photon gas
) will be governed by Bose-Einstein statistics and the distribution of energy will be in the form of a Bose-Einstein distribution. An ideal gas of fermions
will be governed by Fermi-Dirac statistics
and the distribution of energy will be in the form of a Fermi-Dirac distribution.
Gas
Gas is one of the three classical states of matter . Near absolute zero, a substance exists as a solid. As heat is added to this substance it melts into a liquid at its melting point , boils into a gas at its boiling point, and if heated high enough would enter a plasma state in which the electrons...
composed of a set of randomly-moving, non-interacting point particle
Point particle
A point particle is an idealization of particles heavily used in physics. Its defining feature is that it lacks spatial extension: being zero-dimensional, it does not take up space...
s. The ideal gas concept is useful because it obeys the ideal gas law
Ideal gas law
The ideal gas law is the equation of state of a hypothetical ideal gas. It is a good approximation to the behavior of many gases under many conditions, although it has several limitations. It was first stated by Émile Clapeyron in 1834 as a combination of Boyle's law and Charles's law...
, a simplified equation of state
Equation of state
In physics and thermodynamics, an equation of state is a relation between state variables. More specifically, an equation of state is a thermodynamic equation describing the state of matter under a given set of physical conditions...
, and is amenable to analysis under statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
.
At normal conditions such as standard temperature and pressure, most real gas
Gas
Gas is one of the three classical states of matter . Near absolute zero, a substance exists as a solid. As heat is added to this substance it melts into a liquid at its melting point , boils into a gas at its boiling point, and if heated high enough would enter a plasma state in which the electrons...
es behave qualitatively like an ideal gas. Many gases such as air, nitrogen
Nitrogen
Nitrogen is a chemical element that has the symbol N, atomic number of 7 and atomic mass 14.00674 u. Elemental nitrogen is a colorless, odorless, tasteless, and mostly inert diatomic gas at standard conditions, constituting 78.08% by volume of Earth's atmosphere...
, oxygen
Oxygen
Oxygen is the element with atomic number 8 and represented by the symbol O. Its name derives from the Greek roots ὀξύς and -γενής , because at the time of naming, it was mistakenly thought that all acids required oxygen in their composition...
, hydrogen
Hydrogen
Hydrogen is the chemical element with atomic number 1. It is represented by the symbol H. With an average atomic weight of , hydrogen is the lightest and most abundant chemical element, constituting roughly 75% of the Universe's chemical elemental mass. Stars in the main sequence are mainly...
, noble gases, and some heavier gases like carbon dioxide
Carbon dioxide
Carbon dioxide is a naturally occurring chemical compound composed of two oxygen atoms covalently bonded to a single carbon atom...
can be treated like ideal gases within reasonable tolerances. Generally, a gas behaves more like an ideal gas at higher temperature
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
and lower density
Density
The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
(i.e. lower pressure
Pressure
Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
), as the work performed by intermolecular forces becomes less significant compared with the particles' kinetic energy
Kinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
, and the size of the molecules becomes less significant compared to the empty space between them.
The ideal gas model tends to fail at lower temperatures or higher pressures, when intermolecular forces and molecular size become important. It also fails for most heavy gases, such as water vapor
Water vapor
Water vapor or water vapour , also aqueous vapor, is the gas phase of water. It is one state of water within the hydrosphere. Water vapor can be produced from the evaporation or boiling of liquid water or from the sublimation of ice. Under typical atmospheric conditions, water vapor is continuously...
or many refrigerant
Refrigerant
A refrigerant is a substance used in a heat cycle usually including, for enhanced efficiency, a reversible phase change from a liquid to a gas. Traditionally, fluorocarbons, especially chlorofluorocarbons, were used as refrigerants, but they are being phased out because of their ozone depletion...
s. At some point of low temperature and high pressure, real gases undergo a phase transition
Phase transition
A phase transition is the transformation of a thermodynamic system from one phase or state of matter to another.A phase of a thermodynamic system and the states of matter have uniform physical properties....
, such as to a liquid
Liquid
Liquid is one of the three classical states of matter . Like a gas, a liquid is able to flow and take the shape of a container. Some liquids resist compression, while others can be compressed. Unlike a gas, a liquid does not disperse to fill every space of a container, and maintains a fairly...
or a solid
Solid
Solid is one of the three classical states of matter . It is characterized by structural rigidity and resistance to changes of shape or volume. Unlike a liquid, a solid object does not flow to take on the shape of its container, nor does it expand to fill the entire volume available to it like a...
. The model of an ideal gas, however, does not describe or allow phase transitions. These must be modeled by more complex equations of state
Equation of state
In physics and thermodynamics, an equation of state is a relation between state variables. More specifically, an equation of state is a thermodynamic equation describing the state of matter under a given set of physical conditions...
.
The ideal gas model has been explored in both the Newtonian dynamics
Newtonian dynamics
In physics, the Newtonian dynamics is understood as the dynamics of a particle or a small body according to Newton's laws of motion.-Mathematical generalizations:...
(as in "kinetic theory
Kinetic theory
The kinetic theory of gases describes a gas as a large number of small particles , all of which are in constant, random motion. The rapidly moving particles constantly collide with each other and with the walls of the container...
") and in quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
(as a "gas in a box
Gas in a box
In quantum mechanics, the results of the quantum particle in a box can be used to look at the equilibrium situation for a quantum ideal gas in a box which is a box containing a large number of molecules which do not interact with each other except for instantaneous thermalizing collisions...
"). The ideal gas model has also been used to model the behavior of electrons in a metal (in the Drude model
Drude model
The Drude model of electrical conduction was proposed in 1900 by Paul Drude to explain the transport properties of electrons in materials...
and the free electron model
Free electron model
In solid-state physics, the free electron model is a simple model for the behaviour of valence electrons in a crystal structure of a metallic solid. It was developed principally by Arnold Sommerfeld who combined the classical Drude model with quantum mechanical Fermi-Dirac statistics and hence it...
), and it is one of the most important models in statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
.
Types of ideal gas
There are three basic classes of ideal gas:- the classical or Maxwell-Boltzmann ideal gas,
- the ideal quantum Bose gasBose gasAn ideal Bose gas is a quantum-mechanical version of a classical ideal gas. It is composed of bosons, which have an integer value of spin, and obey Bose–Einstein statistics...
, composed of bosons, and - the ideal quantum Fermi gasFermi gasA Fermi gas is an ensemble of a large number of fermions. Fermions, named after Enrico Fermi, are particles that obey Fermi–Dirac statistics. These statistics determine the energy distribution of fermions in a Fermi gas in thermal equilibrium, and is characterized by their number density,...
, composed of fermions.
The classical ideal gas can be separated into two types: The classical thermodynamic ideal gas and the ideal quantum Boltzmann gas. Both are essentially the same, except that the classical thermodynamic ideal gas is based on classical statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
, and certain thermodynamic parameters such as the entropy
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
are only specified to within an undetermined additive constant. The ideal quantum Boltzmann gas overcomes this limitation by taking the limit of the quantum Bose gas and quantum Fermi gas in the limit of high temperature to specify these additive constants. The behavior of a quantum Boltzmann gas is the same as that of a classical ideal gas except for the specification of these constants. The results of the quantum Boltzmann gas are used in a number of cases including the Sackur-Tetrode equation
Sackur-Tetrode equation
The Sackur–Tetrode equation is an expression for the entropy of a monatomic classical ideal gas which incorporates quantum considerations which give a more detailed description of its regime of validity....
for the entropy of an ideal gas and the Saha ionization equation
Saha ionization equation
The Saha ionization equation, also known as the Saha–Langmuir equation, was developed by the Indian astrophysicist Meghnad Saha in 1920, and later by Irving Langmuir. One of the important applications of the equation was in explaining the spectral classification of stars...
for a weakly ionized plasma
Plasma (physics)
In physics and chemistry, plasma is a state of matter similar to gas in which a certain portion of the particles are ionized. Heating a gas may ionize its molecules or atoms , thus turning it into a plasma, which contains charged particles: positive ions and negative electrons or ions...
.
Classical thermodynamic ideal gas
The thermodynamic properties of an ideal gas can be described by two equations:The equation of state
Equation of state
In physics and thermodynamics, an equation of state is a relation between state variables. More specifically, an equation of state is a thermodynamic equation describing the state of matter under a given set of physical conditions...
of a classical ideal gas is the ideal gas law
Ideal gas law
The ideal gas law is the equation of state of a hypothetical ideal gas. It is a good approximation to the behavior of many gases under many conditions, although it has several limitations. It was first stated by Émile Clapeyron in 1834 as a combination of Boyle's law and Charles's law...
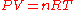
and the internal energy
Internal energy
In thermodynamics, the internal energy is the total energy contained by a thermodynamic system. It is the energy needed to create the system, but excludes the energy to displace the system's surroundings, any energy associated with a move as a whole, or due to external force fields. Internal...
of an ideal gas given by:
where
- P is the pressurePressurePressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
- V is the volume
- n is the amount of substanceAmount of substanceAmount of substance is a standards-defined quantity that measures the size of an ensemble of elementary entities, such as atoms, molecules, electrons, and other particles. It is sometimes referred to as chemical amount. The International System of Units defines the amount of substance to be...
of the gas (in moles) - R is the gas constantGas constantThe gas constant is a physical constant which is featured in many fundamental equations in the physical sciences, such as the ideal gas law and the Nernst equation. It is equivalent to the Boltzmann constant, but expressed in units of energy The gas constant (also known as the molar, universal,...
(8.314 JJouleThe joule ; symbol J) is a derived unit of energy or work in the International System of Units. It is equal to the energy expended in applying a force of one newton through a distance of one metre , or in passing an electric current of one ampere through a resistance of one ohm for one second...
·KKelvinThe kelvin is a unit of measurement for temperature. It is one of the seven base units in the International System of Units and is assigned the unit symbol K. The Kelvin scale is an absolute, thermodynamic temperature scale using as its null point absolute zero, the temperature at which all...
−1molMole (unit)The mole is a unit of measurement used in chemistry to express amounts of a chemical substance, defined as an amount of a substance that contains as many elementary entities as there are atoms in 12 grams of pure carbon-12 , the isotope of carbon with atomic weight 12. This corresponds to a value...
-1) - T is the absolute temperature
- U is the internal energyInternal energyIn thermodynamics, the internal energy is the total energy contained by a thermodynamic system. It is the energy needed to create the system, but excludes the energy to displace the system's surroundings, any energy associated with a move as a whole, or due to external force fields. Internal...
-
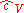is the dimensionless specific heat capacityHeat capacityHeat capacity , or thermal capacity, is the measurable physical quantity that characterizes the amount of heat required to change a substance's temperature by a given amount...
at constant volume, ≈ 3/2 for monatomic gasMonatomic gasIn physics and chemistry, monatomic is a combination of the words "mono" and "atomic," and means "single atom." It is usually applied to gases: a monatomic gas is one in which atoms are not bound to each other....
, 5/2 for diatomicDiatomicDiatomic molecules are molecules composed only of two atoms, of either the same or different chemical elements. The prefix di- means two in Greek. Common diatomic molecules are hydrogen , nitrogen , oxygen , and carbon monoxide . Seven elements exist in the diatomic state in the liquid and solid...
gas and 3 for more complex molecules.
The amount of gas in J
Joule
The joule ; symbol J) is a derived unit of energy or work in the International System of Units. It is equal to the energy expended in applying a force of one newton through a distance of one metre , or in passing an electric current of one ampere through a resistance of one ohm for one second...
·K
Kelvin
The kelvin is a unit of measurement for temperature. It is one of the seven base units in the International System of Units and is assigned the unit symbol K. The Kelvin scale is an absolute, thermodynamic temperature scale using as its null point absolute zero, the temperature at which all...
−1 is
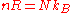
where
- N is the number of gas particles
-
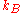is the Boltzmann constant (1.381×10−23J·K−1).
The probability distribution of particles by velocity or energy is given by the Boltzmann distribution
Boltzmann distribution
In chemistry, physics, and mathematics, the Boltzmann distribution is a certain distribution function or probability measure for the distribution of the states of a system. It underpins the concept of the canonical ensemble, providing its underlying distribution...
.
The ideal gas law is an extension of experimentally discovered gas laws
Gas laws
The early gas laws were developed at the end of the 18th century, when scientists began to realize that relationships between the pressure, volume and temperature of a sample of gas could be obtained which would hold for all gases...
. Real fluids at low density
Density
The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
and high temperature
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
approximate the behavior of a classical ideal gas. However, at lower temperatures or a higher density
Density
The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
, a real fluid deviates strongly from the behavior of an ideal gas, particularly as it condenses from a gas into a liquid or solid. The deviation is expressed as a compressibility factor
Compressibility factor
The compressibility factor , also known as the compression factor, is a useful thermodynamic property for modifying the ideal gas law to account for the real gas behavior. In general, deviation from ideal behavior becomes more significant the closer a gas is to a phase change, the lower the...
.
Heat capacity
The heat capacity at constant volume of nR = 1 J·K−1 of any gas, including an ideal gas is: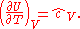This is the dimensionless heat capacity at constant volume, which is generally a function of temperature due to intermolecular forces. For moderate temperatures, the constant for a monoatomic gas is
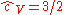while for a diatomic gas it is 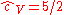. It is seen that macroscopic measurements on heat capacity provide information on the microscopic structure of the molecules.The heat capacity at constant pressure of 1 J·K−1 ideal gas is:
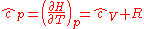
where
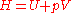is the enthalpyEnthalpy
Enthalpy is a measure of the total energy of a thermodynamic system. It includes the internal energy, which is the energy required to create a system, and the amount of energy required to make room for it by displacing its environment and establishing its volume and pressure.Enthalpy is a...
of the gas.
Sometimes, a distinction is made between an ideal gas, where
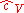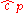and could vary with pressure and temperature, and a perfect gasPerfect gas
In physics, a perfect gas is a theoretical gas that differs from real gases in a way that makes certain calculations easier to handle. Its behavior is more simplified compared to an ideal gas...
, for which this is not the case.
Entropy
Using the results of thermodynamicsThermodynamics
Thermodynamics is a physical science that studies the effects on material bodies, and on radiation in regions of space, of transfer of heat and of work done on or by the bodies or radiation...
only, we can go a long way in determining the expression for the entropy
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
of an ideal gas. This is an important step since, according to the theory of thermodynamic potentials, if we can express the entropy as a function of U (U is a thermodynamic potential) and the volume V, then we will have a complete statement of the thermodynamic behavior of the ideal gas. We will be able to derive both the ideal gas law and the expression for internal energy from it.
Since the entropy is an exact differential
Exact differential
A mathematical differential is said to be exact, as contrasted with an inexact differential, if it is of the form dQ, for some differentiable function Q....
, using the chain rule
Chain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
, the change in entropy when going from a reference state 0 to some other state with entropy S may be written as
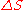where: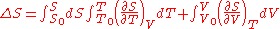where the reference variables may be functions of the number of particles N. Using the definition of the heat capacity
Heat capacity
Heat capacity , or thermal capacity, is the measurable physical quantity that characterizes the amount of heat required to change a substance's temperature by a given amount...
at constant volume for the first differential and the appropriate Maxwell relation for the second we have:
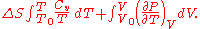
Expressing
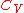in terms of 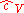as developed in the above section, differentiating the ideal gas equation of state, and integrating yields:where all constants have been incorporated into the logarithm as f(N) which is some function of the particle number N having the same dimensions as
in order that the argument of the logarithm be dimensionless. We now impose the constraint that the entropy be extensive. This will mean that when the extensive parameters (V and N) are multiplied by a constant, the entropy will be multiplied by the same constant. Mathematically: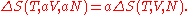From this we find an equation for the function f(N)
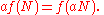
Differentiating this with respect to a, setting a equal to unity, and then solving the differential equation yields f(N):
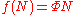
where
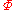is some constant with the dimensions of 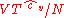. Substituting into the equation for the change in entropy: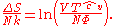This is about as far as we can go using thermodynamics alone. Note that the above equation is flawed — as the temperature approaches zero, the entropy approaches negative infinity, in contradiction to the third law of thermodynamics
Third law of thermodynamics
The third law of thermodynamics is a statistical law of nature regarding entropy:For other materials, the residual entropy is not necessarily zero, although it is always zero for a perfect crystal in which there is only one possible ground state.-History:...
. In the above "ideal" development, there is a critical point, not at absolute zero, at which the argument of the logarithm becomes unity, and the entropy becomes zero. This is unphysical. The above equation is a good approximation only when the argument of the logarithm is much larger than unity — the concept of an ideal gas breaks down at low values of V/N. Nevertheless, there will be a "best" value of the constant in the sense that the predicted entropy is as close as possible to the actual entropy, given the flawed assumption of ideality. It remained for quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
to introduce a reasonable value for the value of
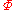which yields the Sackur-Tetrode equationSackur-Tetrode equation
The Sackur–Tetrode equation is an expression for the entropy of a monatomic classical ideal gas which incorporates quantum considerations which give a more detailed description of its regime of validity....
for the entropy of an ideal gas. It too suffers from a divergent entropy at absolute zero, but is a good approximation to an ideal gas over a large range of densities.
Thermodynamic potentials
Since the dimensionless heat capacity at constant pressure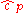 is a constant we can express the entropy in what will prove to be a more convenient form: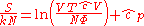where
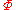is now the undetermined constant. The chemical potentialChemical potential
Chemical potential, symbolized by μ, is a measure first described by the American engineer, chemist and mathematical physicist Josiah Willard Gibbs. It is the potential that a substance has to produce in order to alter a system...
of the ideal gas is calculated from the corresponding equation of state (see thermodynamic potential):
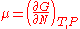
where G is the Gibbs free energy
Gibbs free energy
In thermodynamics, the Gibbs free energy is a thermodynamic potential that measures the "useful" or process-initiating work obtainable from a thermodynamic system at a constant temperature and pressure...
and is equal to
so that: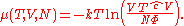The thermodynamic potentials for an ideal gas can now be written as functions of T, V, and N as:
 |
 |
|
 |
 |
 |
 |
 |
 |
 |
 |
 |
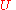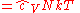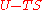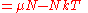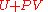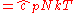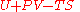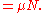The most informative way of writing the potentials is in terms of their natural variables, since each of these equations can be used to derive all of the other thermodynamic variables of the system. In terms of their natural variables, the thermodynamic potentials of a single-species ideal gas are:
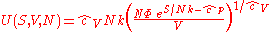
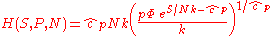
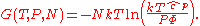
In statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
,
the relationship between the Helmholtz free energy
Helmholtz free energy
In thermodynamics, the Helmholtz free energy is a thermodynamic potential that measures the “useful” work obtainable from a closed thermodynamic system at a constant temperature and volume...
and the
partition function
Partition function (statistical mechanics)
Partition functions describe the statistical properties of a system in thermodynamic equilibrium. It is a function of temperature and other parameters, such as the volume enclosing a gas...
is fundamental, and is used to calculate the
thermodynamic properties
of matters; see
configuration integral
for more details.
Multicomponent systems
By Gibbs' theorem, the entropy of a multicomponent system is equal to the sum of the entropies of each chemical species (assuming no surface effects). The entropy of a multicomponent system will be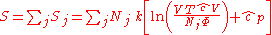where the sum is over all species. Likewise, the free energies are equal to the sums of the free energies of each species so that if Φ is a thermodynamic potential then
where Φj is expressed in terms of its natural variables. For example, the internal energy will be
where N is defined as
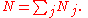
Ideal gasses are not found in the real world. So they are different from real gasses. There are basic assumptions made in the kinetic theory of gasses.
Speed of sound
The speed of sound in an ideal gas is given by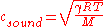where
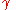is the adiabatic index is the universal gas constant is the temperatureTemperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
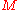is the molar massMolar mass
Molar mass, symbol M, is a physical property of a given substance , namely its mass per amount of substance. The base SI unit for mass is the kilogram and that for amount of substance is the mole. Thus, the derived unit for molar mass is kg/mol...
of the gas.
Equation Table for an Ideal Gas
See Table of thermodynamic equations#Equation Table for an Ideal Gas.Ideal quantum gases
In the above mentioned Sackur-Tetrode equation, the best choice of the entropy constant was found to be proportional to the quantum thermal wavelength of a particle, and the point at which the argument of the logarithm becomes zero is roughly equal to the point at which the average distance between particles becomes equal to the thermal wavelength. In fact, quantumQuantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
theory itself predicts the same thing. Any gas behaves as an ideal gas at high enough temperature and low enough density, but at the point where the Sackur-Tetrode equation
Sackur-Tetrode equation
The Sackur–Tetrode equation is an expression for the entropy of a monatomic classical ideal gas which incorporates quantum considerations which give a more detailed description of its regime of validity....
begins to break down, the gas will begin to behave as a quantum gas, composed of either bosons or fermions. (See the gas in a box
Gas in a box
In quantum mechanics, the results of the quantum particle in a box can be used to look at the equilibrium situation for a quantum ideal gas in a box which is a box containing a large number of molecules which do not interact with each other except for instantaneous thermalizing collisions...
article for a derivation of the ideal quantum gases, including the ideal Boltzmann gas.)
Gases tend to behave as an ideal gas over a wider range of pressures when the temperature reaches the Boyle temperature.
Ideal Boltzmann gas
The ideal Boltzmann gas yields the same results as the classical thermodynamic gas, but makes the following identification for the undetermined constant Φ: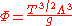where Λ is the thermal de Broglie wavelength of the gas and g is the degeneracy
Degenerate energy level
In physics, two or more different quantum states are said to be degenerate if they are all at the same energy level. Statistically this means that they are all equally probable of being filled, and in Quantum Mechanics it is represented mathematically by the Hamiltonian for the system having more...
of states.
Ideal Bose and Fermi gases
An ideal gas of bosonsBose gas
An ideal Bose gas is a quantum-mechanical version of a classical ideal gas. It is composed of bosons, which have an integer value of spin, and obey Bose–Einstein statistics...
(e.g. a photon gas
Photon gas
In physics, a photon gas is a gas-like collection of photons, which has many of the same properties of a conventional gas like hydrogen or neon - including pressure, temperature, and entropy...
) will be governed by Bose-Einstein statistics and the distribution of energy will be in the form of a Bose-Einstein distribution. An ideal gas of fermions
Fermi gas
A Fermi gas is an ensemble of a large number of fermions. Fermions, named after Enrico Fermi, are particles that obey Fermi–Dirac statistics. These statistics determine the energy distribution of fermions in a Fermi gas in thermal equilibrium, and is characterized by their number density,...
will be governed by Fermi-Dirac statistics
Fermi-Dirac statistics
Fermi–Dirac statistics is a part of the science of physics that describes the energies of single particles in a system comprising many identical particles that obey the Pauli Exclusion Principle...
and the distribution of energy will be in the form of a Fermi-Dirac distribution.
See also
- Compressibility factorCompressibility factorThe compressibility factor , also known as the compression factor, is a useful thermodynamic property for modifying the ideal gas law to account for the real gas behavior. In general, deviation from ideal behavior becomes more significant the closer a gas is to a phase change, the lower the...
- Dynamical billiardsDynamical billiardsA billiard is a dynamical system in which a particle alternates between motion in a straight line and specular reflections from a boundary. When the particle hits the boundary it reflects from it without loss of speed...
- billiard balls as a model of an ideal gas - Table of thermodynamic equationsTable of thermodynamic equationsThe following page is a concise list of common thermodynamic equations and quantities:-Entropy:*~ S = k_B ~, where k_B is the Boltzmann constant, and \Omega denotes the volume of macrostate in the phase space....
- Scale-free ideal gasScale-Free Ideal GasThe scale-free ideal gas is a physical model assuming a collection of non-interacting elements with an stochastic proportional growth. It is the scale-invariant version of an ideal gas...