Einstein solid
Encyclopedia
The Einstein solid is a model of a solid based on two assumptions:
While the assumption that a solid has independent oscillations is very accurate, these oscillations are sound waves or phonons, collective modes involving many atoms. In the Einstein model, each atom oscillates independently. Einstein
was aware that getting the frequency of the actual oscillations would be different, but he nevertheless proposed this theory because it was a particularly clear demonstration that quantum mechanics could solve the specific heat problem in classical mechanics.
in 1907 has great historical relevance. The heat capacity
of solid
s as predicted by the empirical Dulong-Petit law was required by classical mechanics
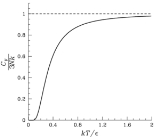
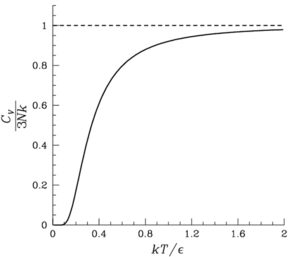
, the specific heat of solids should be independent of temperature. But experiments at low temperatures showed that the heat capacity changes, going to zero at absolute zero. As the temperature goes up, the specific heat goes up until it approaches the Dulong and Petit prediction at high temperature.
By employing Planck's quantization
assumption, Einstein's theory accounted for the observed experimental trend for the first time. Together with the photoelectric effect
, this became one of the most important pieces of evidence for the need of quantization. Einstein used the levels of the quantum mechanical oscillator many years before the advent of modern quantum mechanics
.
In Einstein's model, the specific heat approaches zero exponentially fast at low temperatures. This is because all the oscillations have one common frequency. The correct behavior is found by quantizing the normal modes of the solid in the same way that Einstein suggested. Then the frequencies of the waves are not all the same, and the specific heat goes to zero as a
power law, which matches experiment. This modification is called the Debye Model
, which appeared in 1912.
The heat capacity
of an object at constant volume V is defined through the internal energy
U as
, the temperature of the system, can be found from the entropy
To find the entropy consider a solid made of
atoms, each of which has 3 degrees of freedom. So there are 
quantum harmonic oscillator
s (hereafter SHOs).
Possible energies of an SHO are given by
or, in other words, the energy levels are evenly spaced and one can define a quantum of energy
which is the smallest and only amount by which the energy of an SHO can be incremented. Next, we must compute the multiplicity of the system. That is, compute the number of ways to distribute
quanta of energy among 
SHOs. This task becomes simpler if one thinks of distributing 
pebbles over 
boxes
or separating stacks of pebbles with
partitions
or arranging
pebbles and 
partitions
The last picture is the most telling. The number of arrangements of
objects is 
. So the number of possible arrangements of 
pebbles and 
partitions is 
. However, if partition #2 and partition #5 trade places, no one would notice. The same argument goes for quanta. To obtain the number of possible distinguishable arrangements one has to divide the total number of arrangements by the number of indistinguishable arrangements. There are 
identical quanta arrangements, and 
identical partition arrangements. Therefore, multiplicity of the system is given by
which, as mentioned before, is the number of ways to deposit
quanta of energy into 
oscillators. Entropy
of the system has the form
is a huge number—subtracting one from it has no overall effect whatsoever:
With the help of Stirling's approximation
, entropy can be simplified:
Total energy of the solid is given by
since there are q energy quanta in total in the system in addition to the ground state energy of each oscillator. Some authors, such as Schroeder, omit this ground state energy in their definition of the total energy of an Einstein solid.
We are now ready to compute the temperature
Inverting this formula to find U:
Differentiating with respect to temperature to find
:
or
Although the Einstein model of the solid predicts the heat capacity accurately at high temperatures, it noticeably deviates from experimental values at low temperatures. See Debye model
for how to calculate accurate low-temperature heat capacities.
where
substituting this into the partition function formula yields
This is the partition function of one SHO. Because, statistically, heat capacity, energy, and entropy of the solid are equally distributed among its atoms (SHOs), we can work with this partition function to obtain those quantities and then simply multiply them by
to get the total. Next, let's compute the average energy of each oscillator
where
Therefore
Heat capacity of one oscillator is then
Up to now, we calculated the heat capacity of a unique degree of freedom, which has been modeled as an SHO. The heat capacity of the entire solid is then given by
, where the total number of degree of freedom of the solid is three (for the three directional degree of freedom) times 
, the number of atoms in the solid. One thus obtains
which is algebraically identical to the formula derived in the previous section.
The quantity
has the dimensions of temperature and is a characteristic property of a crystal. It is known as the "Einstein Temperature". Hence, the Einstein Crystal model predicts that the energy and heat capacities of a crystal are universal functions of the dimensionless ratio 
. Similarly, the Debye model predicts a universal function of the ratio 
(see Debye versus Einstein).
- Each atom in the lattice is an independent 3D quantum harmonic oscillatorQuantum harmonic oscillatorThe quantum harmonic oscillator is the quantum-mechanical analog of the classical harmonic oscillator. Because an arbitrary potential can be approximated as a harmonic potential at the vicinity of a stable equilibrium point, it is one of the most important model systems in quantum mechanics...
- All atoms oscillate with the same frequency (contrast with the Debye modelDebye modelIn thermodynamics and solid state physics, the Debye model is a method developed by Peter Debye in 1912 for estimating the phonon contribution to the specific heat in a solid. It treats the vibrations of the atomic lattice as phonons in a box, in contrast to the Einstein model, which treats the...
)
While the assumption that a solid has independent oscillations is very accurate, these oscillations are sound waves or phonons, collective modes involving many atoms. In the Einstein model, each atom oscillates independently. Einstein
Albert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
was aware that getting the frequency of the actual oscillations would be different, but he nevertheless proposed this theory because it was a particularly clear demonstration that quantum mechanics could solve the specific heat problem in classical mechanics.
Historical impact
The original theory proposed by EinsteinAlbert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
in 1907 has great historical relevance. The heat capacity
Heat capacity
Heat capacity , or thermal capacity, is the measurable physical quantity that characterizes the amount of heat required to change a substance's temperature by a given amount...
of solid
Solid
Solid is one of the three classical states of matter . It is characterized by structural rigidity and resistance to changes of shape or volume. Unlike a liquid, a solid object does not flow to take on the shape of its container, nor does it expand to fill the entire volume available to it like a...
s as predicted by the empirical Dulong-Petit law was required by classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
, the specific heat of solids should be independent of temperature. But experiments at low temperatures showed that the heat capacity changes, going to zero at absolute zero. As the temperature goes up, the specific heat goes up until it approaches the Dulong and Petit prediction at high temperature.
By employing Planck's quantization
Quantization (physics)
In physics, quantization is the process of explaining a classical understanding of physical phenomena in terms of a newer understanding known as "quantum mechanics". It is a procedure for constructing a quantum field theory starting from a classical field theory. This is a generalization of the...
assumption, Einstein's theory accounted for the observed experimental trend for the first time. Together with the photoelectric effect
Photoelectric effect
In the photoelectric effect, electrons are emitted from matter as a consequence of their absorption of energy from electromagnetic radiation of very short wavelength, such as visible or ultraviolet light. Electrons emitted in this manner may be referred to as photoelectrons...
, this became one of the most important pieces of evidence for the need of quantization. Einstein used the levels of the quantum mechanical oscillator many years before the advent of modern quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
.
In Einstein's model, the specific heat approaches zero exponentially fast at low temperatures. This is because all the oscillations have one common frequency. The correct behavior is found by quantizing the normal modes of the solid in the same way that Einstein suggested. Then the frequencies of the waves are not all the same, and the specific heat goes to zero as a
power law, which matches experiment. This modification is called the Debye ModelDebye model
In thermodynamics and solid state physics, the Debye model is a method developed by Peter Debye in 1912 for estimating the phonon contribution to the specific heat in a solid. It treats the vibrations of the atomic lattice as phonons in a box, in contrast to the Einstein model, which treats the...
, which appeared in 1912.
Heat capacity (microcanonical ensemble)
Heat capacity
Heat capacity , or thermal capacity, is the measurable physical quantity that characterizes the amount of heat required to change a substance's temperature by a given amount...
of an object at constant volume V is defined through the internal energy
Internal energy
In thermodynamics, the internal energy is the total energy contained by a thermodynamic system. It is the energy needed to create the system, but excludes the energy to displace the system's surroundings, any energy associated with a move as a whole, or due to external force fields. Internal...
U as
, the temperature of the system, can be found from the entropyEntropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
To find the entropy consider a solid made of
atoms, each of which has 3 degrees of freedom. So there are quantum harmonic oscillatorQuantum harmonic oscillator
The quantum harmonic oscillator is the quantum-mechanical analog of the classical harmonic oscillator. Because an arbitrary potential can be approximated as a harmonic potential at the vicinity of a stable equilibrium point, it is one of the most important model systems in quantum mechanics...
s (hereafter SHOs).
Possible energies of an SHO are given by
or, in other words, the energy levels are evenly spaced and one can define a quantum of energy
which is the smallest and only amount by which the energy of an SHO can be incremented. Next, we must compute the multiplicity of the system. That is, compute the number of ways to distribute
quanta of energy among SHOs. This task becomes simpler if one thinks of distributing pebbles over boxes
or separating stacks of pebbles with
partitions
or arranging
pebbles and partitions
The last picture is the most telling. The number of arrangements of
objects is . So the number of possible arrangements of pebbles and partitions is . However, if partition #2 and partition #5 trade places, no one would notice. The same argument goes for quanta. To obtain the number of possible distinguishable arrangements one has to divide the total number of arrangements by the number of indistinguishable arrangements. There are identical quanta arrangements, and identical partition arrangements. Therefore, multiplicity of the system is given bywhich, as mentioned before, is the number of ways to deposit
quanta of energy into oscillators. EntropyEntropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
of the system has the form
is a huge number—subtracting one from it has no overall effect whatsoever:With the help of Stirling's approximation
Stirling's approximation
In mathematics, Stirling's approximation is an approximation for large factorials. It is named after James Stirling.The formula as typically used in applications is\ln n! = n\ln n - n +O\...
, entropy can be simplified:
Total energy of the solid is given by
since there are q energy quanta in total in the system in addition to the ground state energy of each oscillator. Some authors, such as Schroeder, omit this ground state energy in their definition of the total energy of an Einstein solid.
We are now ready to compute the temperature
Inverting this formula to find U:
Differentiating with respect to temperature to find
:or
Although the Einstein model of the solid predicts the heat capacity accurately at high temperatures, it noticeably deviates from experimental values at low temperatures. See Debye model
Debye model
In thermodynamics and solid state physics, the Debye model is a method developed by Peter Debye in 1912 for estimating the phonon contribution to the specific heat in a solid. It treats the vibrations of the atomic lattice as phonons in a box, in contrast to the Einstein model, which treats the...
for how to calculate accurate low-temperature heat capacities.
Heat capacity (canonical ensemble)
Heat capacity can be obtained through the use of the canonical partition function of a single harmonic oscillator (SHO).where
substituting this into the partition function formula yields
This is the partition function of one SHO. Because, statistically, heat capacity, energy, and entropy of the solid are equally distributed among its atoms (SHOs), we can work with this partition function to obtain those quantities and then simply multiply them by
to get the total. Next, let's compute the average energy of each oscillatorwhere
Therefore
Heat capacity of one oscillator is then
Up to now, we calculated the heat capacity of a unique degree of freedom, which has been modeled as an SHO. The heat capacity of the entire solid is then given by
, where the total number of degree of freedom of the solid is three (for the three directional degree of freedom) times , the number of atoms in the solid. One thus obtains
which is algebraically identical to the formula derived in the previous section.
The quantity
has the dimensions of temperature and is a characteristic property of a crystal. It is known as the "Einstein Temperature". Hence, the Einstein Crystal model predicts that the energy and heat capacities of a crystal are universal functions of the dimensionless ratio . Similarly, the Debye model predicts a universal function of the ratio (see Debye versus Einstein).External links
- "Einstein Solid" by Enrique Zeleny, The Wolfram Demonstrations Project.