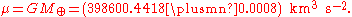Gravitational constant
Encyclopedia
Empirical
The word empirical denotes information gained by means of observation or experimentation. Empirical data are data produced by an experiment or observation....
physical constant
Physical constant
A physical constant is a physical quantity that is generally believed to be both universal in nature and constant in time. It can be contrasted with a mathematical constant, which is a fixed numerical value but does not directly involve any physical measurement.There are many physical constants in...
involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
's law of universal gravitation
Newton's law of universal gravitation
Newton's law of universal gravitation states that every point mass in the universe attracts every other point mass with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between them...
and in Einstein
Albert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
's theory of general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
. It is also known as the universal gravitational constant, Newton's constant, and colloquially Big G. It should not be confused with "little g" (g), which is the local gravitational field
Earth's gravity
The gravity of Earth, denoted g, refers to the acceleration that the Earth imparts to objects on or near its surface. In SI units this acceleration is measured in metres per second per second or equivalently in newtons per kilogram...
(equivalent to the free-fall acceleration), especially that at the Earth's surface; see Gravity of Earth and Standard gravity
Standard gravity
Standard gravity, or standard acceleration due to free fall, usually denoted by g0 or gn, is the nominal acceleration of an object in a vacuum near the surface of the Earth. It is defined as precisely , or about...
.
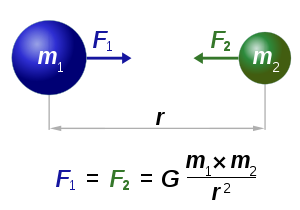
According to the law of universal gravitation, the attractive force
Force
In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
(F) between two bodies is proportional to the product of their mass
Mass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
es (m1 and m2), and inversely proportional to the square of the distance (r) between them:

The constant of proportionality, G, is the gravitational constant.
The gravitational constant is perhaps the most difficult physical constant to measure to high accuracy. In SI
Si
Si, si, or SI may refer to :- Measurement, mathematics and science :* International System of Units , the modern international standard version of the metric system...
units, the 2010 CODATA-recommended value of the gravitational constant (with standard uncertainty in parentheses) is:

with relative standard uncertainty , or 1 part in 8300.
Dimensions, units and magnitude
The dimensions assigned to the gravitational constant in the equation above—lengthLength
In geometric measurements, length most commonly refers to the longest dimension of an object.In certain contexts, the term "length" is reserved for a certain dimension of an object along which the length is measured. For example it is possible to cut a length of a wire which is shorter than wire...
cubed, divided by mass
Mass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
and by time
Time
Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
squared (in SI units, metre
Metre
The metre , symbol m, is the base unit of length in the International System of Units . Originally intended to be one ten-millionth of the distance from the Earth's equator to the North Pole , its definition has been periodically refined to reflect growing knowledge of metrology...
s cubed per kilogram
Kilogram
The kilogram or kilogramme , also known as the kilo, is the base unit of mass in the International System of Units and is defined as being equal to the mass of the International Prototype Kilogram , which is almost exactly equal to the mass of one liter of water...
per second
Second
The second is a unit of measurement of time, and is the International System of Units base unit of time. It may be measured using a clock....
squared)—are those needed to balance the units of measurements in gravitational equations. However, these dimensions have fundamental significance in terms of Planck units
Planck units
In physics, Planck units are physical units of measurement defined exclusively in terms of five universal physical constants listed below, in such a manner that these five physical constants take on the numerical value of 1 when expressed in terms of these units. Planck units elegantly simplify...
: when expressed in SI units, the gravitational constant is dimensionally and numerically equal to the cube of the Planck length divided by the Planck mass and by the square of Planck time
Planck time
In physics, the Planck time, , is the unit of time in the system of natural units known as Planck units. It is the time required for light to travel, in a vacuum, a distance of 1 Planck length...
.
In natural units
Natural units
In physics, natural units are physical units of measurement based only on universal physical constants. For example the elementary charge e is a natural unit of electric charge, or the speed of light c is a natural unit of speed...
, of which Planck units
Planck units
In physics, Planck units are physical units of measurement defined exclusively in terms of five universal physical constants listed below, in such a manner that these five physical constants take on the numerical value of 1 when expressed in terms of these units. Planck units elegantly simplify...
are perhaps the best example, G and other physical constants such as c (the speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
) may be set equal to 1.
In many secondary school texts, the dimensions of G are derived from force in order to assist student comprehension:
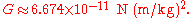
In cgs, G can be written as:
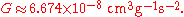
G can also be given as:

Given the fact that the period P of an object in circular orbit around a spherical object obeys

where V is the volume inside the radius of the orbit, we see that
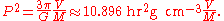
This way of expressing G shows the relationship between the average density of a planet and the period of a satellite orbiting just above its surface.
In some fields of astrophysics
Astrophysics
Astrophysics is the branch of astronomy that deals with the physics of the universe, including the physical properties of celestial objects, as well as their interactions and behavior...
where distances are measured in parsec
Parsec
The parsec is a unit of length used in astronomy. It is about 3.26 light-years, or just under 31 trillion kilometres ....
s (pc), velocities in kilometers per second (km/s) and masses in solar units
Solar mass
The solar mass , , is a standard unit of mass in astronomy, used to indicate the masses of other stars and galaxies...
, it is useful to express G as:
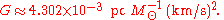
The gravitational force is extremely weak compared with other fundamental forces. For example, the gravitational force between an electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
and proton
Proton
The proton is a subatomic particle with the symbol or and a positive electric charge of 1 elementary charge. One or more protons are present in the nucleus of each atom, along with neutrons. The number of protons in each atom is its atomic number....
1 meter apart is approximately 10−67 newtons, while the electromagnetic force between the same two particles is approximately 10−28 newtons. Both these forces are weak when compared with the forces we are able to experience directly, but the electromagnetic force in this example is some 39 orders of magnitude (i.e., 1039) greater than the force of gravity — roughly the same ratio as the mass of the Sun
Sun
The Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields...
compared to a microgram
Microgram
In the metric system, a microgram is a unit of mass equal to one millionth of a gram , or 1/1000 of a milligram. It is one of the smallest units of mass commonly used...
mass.
History of measurement
The gravitational constant appears in Newton's law of universal gravitationNewton's law of universal gravitation
Newton's law of universal gravitation states that every point mass in the universe attracts every other point mass with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between them...
, but it was not measured until 71 years after Newton's death by Henry Cavendish
Henry Cavendish
Henry Cavendish FRS was a British scientist noted for his discovery of hydrogen or what he called "inflammable air". He described the density of inflammable air, which formed water on combustion, in a 1766 paper "On Factitious Airs". Antoine Lavoisier later reproduced Cavendish's experiment and...
with his Cavendish experiment
Cavendish experiment
The Cavendish experiment, performed in 1797–98 by British scientist Henry Cavendish was the first experiment to measure the force of gravity between masses in the laboratory, and the first to yield accurate values for the gravitational constant. Because of the unit conventions then in use,...
, performed in 1798 (Philosophical Transactions 1798). Cavendish measured G implicitly, using a torsion balance invented by the geologist Rev. John Michell
John Michell
John Michell was an English natural philosopher and geologist whose work spanned a wide range of subjects from astronomy to geology, optics, and gravitation. He was both a theorist and an experimenter....
. He used a horizontal torsion beam with lead balls whose inertia (in relation to the torsion constant) he could tell by timing the beam's oscillation. Their faint attraction to other balls placed alongside the beam was detectable by the deflection it caused. Cavendish's aim was not actually to measure the gravitational constant, but rather to measure the Earth's density relative to water, through the precise knowledge of the gravitational interaction. In retrospect, the density that Cavendish calculated implies a value for G of 6.754 × 10−11 m3 kg−1 s−2.
The accuracy of the measured value of G has increased only modestly since the original Cavendish experiment. G is quite difficult to measure, as gravity is much weaker than other fundamental forces, and an experimental apparatus cannot be separated from the gravitational influence of other bodies. Furthermore, gravity has no established relation to other fundamental forces, so it does not appear possible to calculate it indirectly from other constants that can be measured more accurately, as is done in some other areas of physics. Published values of G have varied rather broadly, and some recent measurements of high precision are, in fact, mutually exclusive.
In the January 5, 2007 issue of Science
Science (journal)
Science is the academic journal of the American Association for the Advancement of Science and is one of the world's top scientific journals....
(page 74), the report "Atom Interferometer Measurement of the Newtonian Constant of Gravity" (J. B. Fixler, G. T. Foster, J. M. McGuirk, and M. A. Kasevich) describes a new measurement of the gravitational constant. According to the abstract: "Here, we report a value of G = 6.693 × 10−11 cubic meters per kilogram second squared, with a standard error of the mean of ±0.027 × 10−11 and a systematic error of ±0.021 × 10−11 cubic meters per kilogram second squared."
The GM product
The quantity GM—the product of the gravitational constant and the mass of a given astronomical body such as the Sun or the Earth—is known as the standard gravitational parameter and is denoted . Depending on the body concerned, it may also be called the geocentric or heliocentric gravitational constant, among other names.
. Depending on the body concerned, it may also be called the geocentric or heliocentric gravitational constant, among other names.This quantity gives a convenient simplification of various gravity-related formulas. Also, for celestial bodies such as the Earth and the Sun, the value of the product GM is known more accurately than each factor independently. Indeed, the limited accuracy available for G often limits the accuracy of scientific determination of such masses in the first place.
For Earth, using M⊕ as the symbol for the mass of the Earth, we have
Calculations in celestial mechanics
Celestial mechanics
Celestial mechanics is the branch of astronomy that deals with the motions of celestial objects. The field applies principles of physics, historically classical mechanics, to astronomical objects such as stars and planets to produce ephemeris data. Orbital mechanics is a subfield which focuses on...
can also be carried out using the unit of solar mass
Solar mass
The solar mass , , is a standard unit of mass in astronomy, used to indicate the masses of other stars and galaxies...
rather than the standard SI unit kilogram. In this case we use the Gaussian gravitational constant
Gaussian gravitational constant
The Gaussian gravitational constant is an astronomical constant first proposed by German polymath Carl Friedrich Gauss in his 1809 work Theoria motus corporum coelestium in sectionibus conicis solem ambientum , although he had already used the concept to great success in predicting the...
which is k2, where

and
 is the astronomical unit
is the astronomical unitAstronomical unit
An astronomical unit is a unit of length equal to about or approximately the mean Earth–Sun distance....
;
 is the mean solar day;
is the mean solar day; is the solar mass
is the solar massSolar mass
The solar mass , , is a standard unit of mass in astronomy, used to indicate the masses of other stars and galaxies...
.
If instead of mean solar day we use the sidereal year
Sidereal year
A sidereal year is the time taken by the Earth to orbit the Sun once with respect to the fixed stars. Hence it is also the time taken for the Sun to return to the same position with respect to the fixed stars after apparently travelling once around the ecliptic. It was equal to at noon 1 January...
as our time unit, the value of ks is very close to 2π
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
(k = 6.28315).
The standard gravitational parameter GM appears as above in Newton's law of universal gravitation, as well as in formulas for the deflection of light caused by gravitational lensing, in Kepler's laws of planetary motion
Kepler's laws of planetary motion
In astronomy, Kepler's laws give a description of the motion of planets around the Sun.Kepler's laws are:#The orbit of every planet is an ellipse with the Sun at one of the two foci....
, and in the formula for escape velocity
Escape velocity
In physics, escape velocity is the speed at which the kinetic energy plus the gravitational potential energy of an object is zero gravitational potential energy is negative since gravity is an attractive force and the potential is defined to be zero at infinity...
.
External links
- Newtonian constant of gravitation G at the National Institute of Standards and TechnologyNational Institute of Standards and TechnologyThe National Institute of Standards and Technology , known between 1901 and 1988 as the National Bureau of Standards , is a measurement standards laboratory, otherwise known as a National Metrological Institute , which is a non-regulatory agency of the United States Department of Commerce...
References on Constants, Units, and Uncertainty - The Controversy over Newton's Gravitational Constant — additional commentary on measurement problems
- The Gravitational Constant