
Dynamical billiards
Encyclopedia
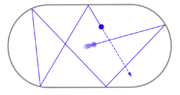
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
in which a particle alternates between motion in a straight line and specular reflection
Specular reflection
Specular reflection is the mirror-like reflection of light from a surface, in which light from a single incoming direction is reflected into a single outgoing direction...
s from a boundary. When the particle hits the boundary it reflects from it without loss of speed
Speed
In kinematics, the speed of an object is the magnitude of its velocity ; it is thus a scalar quantity. The average speed of an object in an interval of time is the distance traveled by the object divided by the duration of the interval; the instantaneous speed is the limit of the average speed as...
. Billiard dynamical systems are Hamiltonian
Hamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
idealizations of the game of billiards
Billiards
Cue sports , also known as billiard sports, are a wide variety of games of skill generally played with a cue stick which is used to strike billiard balls, moving them around a cloth-covered billiards table bounded by rubber .Historically, the umbrella term was billiards...
, but where the region contained by the boundary can have shapes other than rectangular and even be multidimensional. Dynamical billiards may also be studied on non-Euclidean geometries
Non-Euclidean geometry
Non-Euclidean geometry is the term used to refer to two specific geometries which are, loosely speaking, obtained by negating the Euclidean parallel postulate, namely hyperbolic and elliptic geometry. This is one term which, for historical reasons, has a meaning in mathematics which is much...
; indeed, the very first studies of billiards established their ergodic motion
Ergodic theory
Ergodic theory is a branch of mathematics that studies dynamical systems with an invariant measure and related problems. Its initial development was motivated by problems of statistical physics....
on surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
s of constant negative curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
. The study of billiards which are kept out of a region, rather than being kept in a region, is known as outer billiard theory.
The motion of the particle in the billiard is a straight line, with constant energy, between reflections with the boundary (a geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
if the Riemannian metric of the billiard table is not flat). All reflections
Reflection (physics)
Reflection is the change in direction of a wavefront at an interface between two differentmedia so that the wavefront returns into the medium from which it originated. Common examples include the reflection of light, sound and water waves...
are specular
Specular reflection
Specular reflection is the mirror-like reflection of light from a surface, in which light from a single incoming direction is reflected into a single outgoing direction...
: the angle of incidence
Angle of incidence
Angle of incidence is a measure of deviation of something from "straight on", for example:* in the approach of a ray to a surface, or* the angle at which the wing or horizontal tail of an airplane is installed on the fuselage, measured relative to the axis of the fuselage.-Optics:In geometric...
just before the collision is equal to the angle of reflection just after the collision. The sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of reflections is described by the billiard map that completely characterizes the motion of the particle.
Billiards capture all the complexity of Hamiltonian systems, from integrability
Integrable system
In mathematics and physics, there are various distinct notions that are referred to under the name of integrable systems.In the general theory of differential systems, there is Frobenius integrability, which refers to overdetermined systems. In the classical theory of Hamiltonian dynamical...
to chaotic motion
Chaos theory
Chaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...
, without the difficulties of integrating the equations of motion to determine its Poincaré map
Poincaré map
In mathematics, particularly in dynamical systems, a first recurrence map or Poincaré map, named after Henri Poincaré, is the intersection of a periodic orbit in the state space of a continuous dynamical system with a certain lower dimensional subspace, called the Poincaré section, transversal to...
. Birkhoff
George David Birkhoff
-External links:* − from National Academies Press, by Oswald Veblen....
showed that a billiard system with an elliptic
Ellipse
In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
table is integrable.
Equations of motion
The HamiltonianHamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
for a particle of mass m moving freely without friction on a surface is:

where
 is a potential designed to be zero inside the region
is a potential designed to be zero inside the region  in which the particle can move, and infinity otherwise:
in which the particle can move, and infinity otherwise:
This form of the potential guarantees a specular reflection
Specular reflection
Specular reflection is the mirror-like reflection of light from a surface, in which light from a single incoming direction is reflected into a single outgoing direction...
on the boundary. The kinetic term guarantees that the particle moves in a straight line, without any change in energy. If the particle is to move on a non-Euclidean manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
, then the Hamiltonian is replaced by:

where
 is the metric tensor
is the metric tensorMetric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
at point
 . Because of the very simple structure of this Hamiltonian, the equations of motion for the particle, the Hamilton–Jacobi equation
. Because of the very simple structure of this Hamiltonian, the equations of motion for the particle, the Hamilton–Jacobi equationHamilton–Jacobi equation
In mathematics, the Hamilton–Jacobi equation is a necessary condition describing extremal geometry in generalizations of problems from the calculus of variations. In physics, the Hamilton–Jacobi equation is a reformulation of classical mechanics and, thus, equivalent to other formulations such as...
s, are nothing other than the geodesic equations on the manifold: the particle moves along geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
s.
Hadamard's billiards
Hadamard's billiards concern the motion of a free point particle on a surface of constant negative curvature, in particular, the simplest compact Riemann surfaceRiemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
with negative curvature, a surface of genus 2 (a two-holed donut). The model is exactly solvable, and is given by the geodesic flow on the surface. It is the earliest example of deterministic chaos ever studied, having been introduced by Jacques Hadamard
Jacques Hadamard
Jacques Salomon Hadamard FRS was a French mathematician who made major contributions in number theory, complex function theory, differential geometry and partial differential equations.-Biography:...
in 1898.
Artin's billiard
Artin's billiard considers the free motion of a point particle on a surface of constant negative curvature, in particular, the simplest non-compact Riemann surfaceRiemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
, a surface with one cusp. It is notable for being exactly solvable, and yet not only ergodic but also strongly mixing
Mixing (mathematics)
In mathematics, mixing is an abstract concept originating from physics: the attempt to describe the irreversible thermodynamic process of mixing in the everyday world: mixing paint, mixing drinks, etc....
. It is an example of an Anosov system. This system was first studied by Emil Artin
Emil Artin
Emil Artin was an Austrian-American mathematician of Armenian descent.-Parents:Emil Artin was born in Vienna to parents Emma Maria, née Laura , a soubrette on the operetta stages of Austria and Germany, and Emil Hadochadus Maria Artin, Austrian-born of Armenian descent...
in 1924.
Sinai billiard
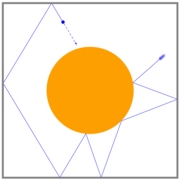
The billiard was introduced by Yakov G. Sinai
Yakov G. Sinai
Yakov Grigorevich Sinai is an influential mathematician working in the theory of dynamical systems, in mathematical physics and in probability theory. His work has shaped the modern metric theory of dynamical systems...
as an example of an interacting Hamiltonian system
Hamiltonian system
In physics and classical mechanics, a Hamiltonian system is a physical system in which forces are momentum invariant. Hamiltonian systems are studied in Hamiltonian mechanics....
that displays physical thermodynamic properties: all of its possible trajectories are ergodic and it has a positive Lyapunov exponent
Lyapunov exponent
In mathematics the Lyapunov exponent or Lyapunov characteristic exponent of a dynamical system is a quantity that characterizes the rate of separation of infinitesimally close trajectories...
. As a model of a classical gas, the Sinai billiard is sometimes called the Lorentz gas.
Sinai's great achievement with this model was to show that the classical Boltzmann–Gibbs ensemble for an ideal gas
Ideal gas
An ideal gas is a theoretical gas composed of a set of randomly-moving, non-interacting point particles. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is amenable to analysis under statistical mechanics.At normal conditions such as...
is essentially the maximally chaotic Hadamard billiards.
Bunimovich stadium
The table called the Bunimovich stadium is a rectangle capped by semicircles. Until it was introduced by Leonid BunimovichLeonid Bunimovich
Leonid Bunimovich is a Russian mathematician, currently residing in the U.S., who specializes in dynamical systems and known for his discovery of focusing chaotic billiards and for the Bunimovich mushroom, a dynamical billiard with mixed regular and chaotic dynamics...
, billiards with positive Lyapunov exponent
Lyapunov exponent
In mathematics the Lyapunov exponent or Lyapunov characteristic exponent of a dynamical system is a quantity that characterizes the rate of separation of infinitesimally close trajectories...
s were thought to need convex scatters, such as the disk in the Sinai billiard, to produce the exponential divergence of orbits. Bunimovich showed that by considering the orbits beyond the focusing point of a concave region it was possible to obtain exponential divergence.
Generalized billiards
Generalized billiards (GB) describe a motion of a mass point (a particle) inside a closed domain with the piece-wise smooth boundary
with the piece-wise smooth boundary  . On the boundary
. On the boundary  the velocity of point is transformed as the particle underwent the action of generalized billiard law. GB were introduced by Lev D. Pustyl'nikov in the general case, and, in the case when
the velocity of point is transformed as the particle underwent the action of generalized billiard law. GB were introduced by Lev D. Pustyl'nikov in the general case, and, in the case when  is a parallelepiped in connection with the justification of the second law of thermodynamics (the law of entropy increase). From the physical point of view, GB describe a gas consisting of finitely many particles moving in a vessel, while the walls of the vessel heat up or cool down. The essence of the generalization is the following. As the particle hits the boundary
is a parallelepiped in connection with the justification of the second law of thermodynamics (the law of entropy increase). From the physical point of view, GB describe a gas consisting of finitely many particles moving in a vessel, while the walls of the vessel heat up or cool down. The essence of the generalization is the following. As the particle hits the boundary  , its velocity transforms with the help of a given function
, its velocity transforms with the help of a given function  , defined on the direct product
, defined on the direct product  (where
(where  is the real line,
is the real line,  is a point of the boundary and
is a point of the boundary and  is time), according to the following law. Suppose that the trajectory of the particle, which moves with the velocity
is time), according to the following law. Suppose that the trajectory of the particle, which moves with the velocity  , intersects
, intersects  at the point
at the point  at time
at time  . Then at time
. Then at time  the particle acquires the velocity
the particle acquires the velocity  , as if it underwent an elastic push from the infinitely-heavy plane
, as if it underwent an elastic push from the infinitely-heavy plane  , which is tangent to
, which is tangent to  at the point
at the point  , and at time
, and at time  moves along the normal to
moves along the normal to  at
at  with the velocity
with the velocity  . We emphasize that the position of the boundary itself is fixed, while its action upon the particle is defined through the function
. We emphasize that the position of the boundary itself is fixed, while its action upon the particle is defined through the function  .
.We take the positive direction of motion of the plane
 to be towards the interior of
to be towards the interior of  . Thus if the derivative
. Thus if the derivative  , then the particle accelerates after the impact.
, then the particle accelerates after the impact.If the velocity
 , acquired by the particle as the result of the above reflection law, is directed to the interior of the domain
, acquired by the particle as the result of the above reflection law, is directed to the interior of the domain  , then the particle will leave the boundary and continue moving in
, then the particle will leave the boundary and continue moving in  until the next collision with
until the next collision with  . If the velocity
. If the velocity  is directed towards the outside of
is directed towards the outside of  , then the particle remains on
, then the particle remains on  at the point
at the point  until at some time
until at some time  the interaction with the boundary will force the particle to leave it.
the interaction with the boundary will force the particle to leave it.If the function
 does not depend on time
does not depend on time  , i.e.,
, i.e.,  , the generalized billiard coincides with the classical one.
, the generalized billiard coincides with the classical one.This generalized reflection law is very natural. First, it reflects an obvious fact that the walls of the vessel with gas are motionless. Second the action of the wall on the particle is still the classical elastic push. In the essence, we consider infinitesimally moving boundaries with given velocities.
It is considered the reflection from the boundary
 both in the framework of classical mechanics (Newtonian case) and the theory of relativity (relativistic case).
both in the framework of classical mechanics (Newtonian case) and the theory of relativity (relativistic case).Main results: in the Newtonian case the energy of particle is bounded, the Gibbs entropy is a constant, (in Notes) and in relativistic case the energy of particle, the Gibbs entropy, the entropy with respect to the phase volume grow to infinity, (in Notes), references to generalized billiards.
Quantum chaos
The quantum version of the billiards is readily studied in several ways. The classical Hamiltonian for the billiards, given above, is replaced by the stationary-state Schrödinger equationSchrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
 or, more precisely,
or, more precisely,
where
 is the Laplacian. The potential that is infinite outside the region
is the Laplacian. The potential that is infinite outside the region  but zero inside it translates to the Dirichlet boundary conditions:
but zero inside it translates to the Dirichlet boundary conditions:
As usual, the wavefunctions are taken to be orthonormal:

Curiously, the free-field Schrödinger equation is the same as the Helmholtz equation
Helmholtz equation
The Helmholtz equation, named for Hermann von Helmholtz, is the elliptic partial differential equation\nabla^2 A + k^2 A = 0where ∇2 is the Laplacian, k is the wavenumber, and A is the amplitude.-Motivation and uses:...
,

with

This implies that two and three-dimensional quantum billiards can be modelled by the classical resonance modes of a radar cavity of a given shape, thus opening a door to experimental verification. (The study of radar cavity modes must be limited to the transverse magnetic (TM) modes, as these are the ones obeying the Dirichlet boundary conditions).
The semi-classical limit corresponds to
 which can be seen to be equivalent to
which can be seen to be equivalent to  , the mass increasing so that it behaves classically.
, the mass increasing so that it behaves classically.As a general statement, one may say that whenever the classical equations of motion are integrable (e.g. rectangular or circular billiard tables), then the quantum-mechanical version of the billiards is completely solvable. When the classical system is chaotic, then the quantum system is generally not exactly solvable, and presents numerous difficulties in its quantization and evaluation. The general study of chaotic quantum systems is known as quantum chaos
Quantum chaos
Quantum chaos is a branch of physics which studies how chaotic classical dynamical systems can be described in terms of quantum theory. The primary question that quantum chaos seeks to answer is, "What is the relationship between quantum mechanics and classical chaos?" The correspondence principle...
.
A particularly striking example of scarring on an elliptical table is given by the observation of the so-called quantum mirage
Quantum mirage
In physics, a quantum mirage is a peculiar result in quantum chaos. Every system of quantum dynamical billiards will exhibit an effect called scarring, where the quantum probability density shows traces of the paths a classical billiard ball would take...
.
Applications
The most practical application of theory of quantum billiards is related with double-clad fiberDouble-clad fiber
Double-clad fiber is a class of optical fiber with a structure consisting of three layers of optical material instead of the usual two. The inner-most layer is called the core. It is surrounded by the inner cladding, which is surrounded by the outer cladding...
s.
In such a fiber laser
Fiber laser
A fiber laser or fibre laser is a laser in which the active gain medium is an optical fiber doped with rare-earth elements such as erbium, ytterbium, neodymium, dysprosium, praseodymium, and thulium. They are related to doped fiber amplifiers, which provide light amplification without lasing...
, the small core with low Numerical Aperture
Numerical aperture
In optics, the numerical aperture of an optical system is a dimensionless number that characterizes the range of angles over which the system can accept or emit light. By incorporating index of refraction in its definition, NA has the property that it is constant for a beam as it goes from one...
confines the signal, and the wide cladding confines the multi-mode
pump. In the paraxial approximation
Paraxial approximation
In geometric optics, the paraxial approximation is a small-angle approximation used in Gaussian optics and ray tracing of light through an optical system ....
, the complex field of pump in the cladding behaves like a wave function in the quantum billiard.
The modes of the cladding with scarring may avoid the core, and symmetrical configurations enhance this effect.
The chaotic fibers
provide good coupling; in the first approximation, such a fiber can be described with the same equations as an idealized billiard.
The coupling is especially poor in fibers with circular symmetry while the spiral-shaped fiber—with the core close to the chunk of the spiral—shows good coupling properties. The small spiral deformation forces all the scars to be coupled with the core.
See also
- Fermi–Ulam modelFermi–Ulam modelThe Fermi–Ulam model is a dynamical system that was introduced by Polish mathematician Stanislaw Ulam in 1961.FUM is a variant of Enrico Fermi's primary work on acceleration of cosmic rays, namely Fermi acceleration. The system consists of a particle that collides elastically between a fixed...
(billiards with oscillating walls) - Lubachevsky-Stillinger algorithmLubachevsky-Stillinger algorithmLubachevsky-Stillinger algorithm isa numerical procedure that simulates or imitatesa physical process of compressing an assemblyof hard particles...
of compression simulates hard spheres colliding not only with the boundaries but also among themselves while growing in sizes
Sinai's billiards
(in English, Sov. Math Dokl. 4 (1963) pp. 1818–1822).- Ya. G. Sinai, "Dynamical Systems with Elastic Reflections", Russian Math. Surveys, 25, (1970) pp. 137–191.
- V. I. Arnold and A. Avez, Théorie ergodique des systèms dynamiques, (1967), Gauthier-Villars, Paris. (English edition: Benjamin-Cummings, Reading, Mass. 1968). (Provides discussion and references for Sinai's billiards.)
- D. Heitmann, J.P. Kotthaus, "The Spectroscopy of Quantum Dot Arrays", Physics Today (1993) pp. 56–63. (Provides a review of experimental tests of quantum versions of Sinai's billiards realized as nano-scale (mesoscopic) structures on silicon wafers.)
- S. Sridhar and W. T. Lu, "Sinai Billiards, Ruelle Zeta-functions and Ruelle Resonances: Microwave Experiments", (2002) Journal of Statistical Physics, Vol. 108 Nos. 5/6, pp. 755–766.
- Linas Vepstas, Sinai's Billiards, (2001). (Provides ray-traced images of Sinai's billiards in three-dimensional space. These images provide a graphic, intuitive demonstration of the strong ergodicity of the system.)
Strange billiards
- T. Schürmann and I. Hoffmann, The entropy of strange billiards inside n-simplexes. J. Phys. A28, page 5033ff, 1995. PDF-Document
Bunimovich stadium
- L.A.Bunimovich, "On the Ergodic Properties of Nowhere Dispersing Billiards", Commun Math Phys, 65 (1979) pp. 295–312.
- L.A.Bunimovich and Ya. G. Sinai, "Markov Partitions for Dispersed Billiards", Commun Math Phys, 78 (1980) pp. 247–280.
- Flash animation illustrating the chaotic Bunimovich Stadium
Generalized billiards
- M. V. Deryabin and L. D. Pustyl'nikov, "Generalized relativistic billiards", Reg. and Chaotic Dyn. 8(3), pp. 283–296 (2003).
- M. V. Deryabin and L. D. Pustyl'nikov, "On Generalized Relativistic Billiards in External Force Fields", Letters in Mathematical Physics, 63(3), pp. 195–207 (2003).
- M. V. Deryabin and L. D. Pustyl'nikov, "Exponential attractors in generalized relativistic billiards", Comm. Math. Phys. 248(3), pp. 527–552 (2004).
External links
- Simulation of the Sinai Billiard (Stephan Matthiesen)

