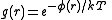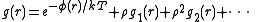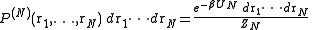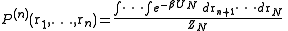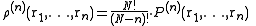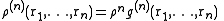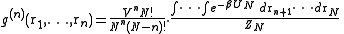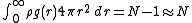Radial distribution function
Encyclopedia
In statistical mechanics
, a radial distribution function (RDF), (or pair correlation function) g(r), describes how the atomic density varies as a function of the distance from one particular atom.
More precisely, if there is an atom at the origin O, and if n = N/V is the average number density, then the local density at distance r from O is ng(r).
Given a potential energy
function, the radial distribution function can be found either via computer simulation methods like the Monte Carlo method
, or via the Ornstein-Zernike equation, using approximative closure relations like the Perckus-Yevick approximation or the Hypernetted Chain Theory
.
The virial equation for the pressure:
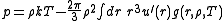
The energy equation: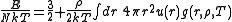
The compressibility equation
: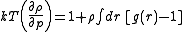
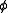 (r) that an atom at P feels owing to the presence of an atom at O. Using the Boltzmann distribution law:
(r) that an atom at P feels owing to the presence of an atom at O. Using the Boltzmann distribution law:
If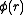 were zero for all r – i.e., if the atoms did not exert any influence on each other, then g(r) = 1 for all r. Then the mean local density would be equal to the mean density
were zero for all r – i.e., if the atoms did not exert any influence on each other, then g(r) = 1 for all r. Then the mean local density would be equal to the mean density 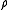 : the presence of an atom at O would not influence the presence or absence of any other atom and the gas would be ideal. As long as there is a
: the presence of an atom at O would not influence the presence or absence of any other atom and the gas would be ideal. As long as there is a 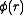 the mean local density will always be different from the mean density
the mean local density will always be different from the mean density  due to the interactions between atoms.
due to the interactions between atoms.
When the density of the gas gets higher, the low-density limit is not applicable anymore because the atoms attracted to and repelled by the atom at O also repel and attract each other. The correction terms needed to correctly describe g(r) resemble the virial equation, which is an expansion in the density:
in which additional functions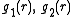 appear which may depend on temperature
appear which may depend on temperature 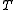 and distance
and distance  but not on density,
but not on density, 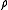 .
.
or x-ray scattering diffraction data. For an example of an RDF experiment see Eigen vs. Zundel structures in HCl solution, 2006
It is additionally possible to calculate g(r) experimentally by extracting particle positions from video or confocal microscopy, as detailed in:
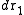 , atom 2 in
, atom 2 in 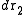 , etc., is given by
, etc., is given by
where and
and 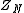 is the configurational integral. To obtain the probability of finding atom 1 in
is the configurational integral. To obtain the probability of finding atom 1 in 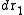 and atom n in
and atom n in 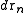 , irrespective of the remaining N − n atoms, one has to integrate (7) over the coordinates of atoms n + 1 through N:
, irrespective of the remaining N − n atoms, one has to integrate (7) over the coordinates of atoms n + 1 through N:
Now the probability that any atom is in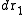 and any atom in
and any atom in 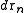 , irrespective of the rest of the atoms, is
, irrespective of the rest of the atoms, is
For n = 1 the one-particle distribution function is obtained which, for a crystal, is a periodic function with sharp maxima at the lattice sites. For a (homogeneous) liquid:
It is now time to introduce a correlation function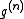 by
by
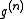 is called a correlation function, since if the atoms are independent from each other
is called a correlation function, since if the atoms are independent from each other 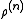 would simply equal
would simply equal 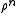 and therefore
and therefore 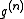 corrects for the correlation between atoms.
corrects for the correlation between atoms.
From (9) it can be shown that
In the theory of liquids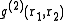 is of special importance for it can be determined experimentally using X-ray diffraction. If the liquid contains spherically symmetric atoms
is of special importance for it can be determined experimentally using X-ray diffraction. If the liquid contains spherically symmetric atoms 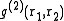 depends only on the relative distance between atoms,
depends only on the relative distance between atoms, 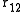 . People usually drop the subscripts:
. People usually drop the subscripts: 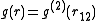 . Now
. Now 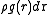 is the probability of finding an atom at r given that there is an atom at the origin of r. Note that this probability is not normalized:
is the probability of finding an atom at r given that there is an atom at the origin of r. Note that this probability is not normalized:
In fact, this equation gives us the number of atoms between r and r + dr about a central atom.
Currently, information on how to obtain the higher order distribution functions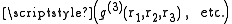 is not available, and scientists rely on approximations based upon statistical mechanics
is not available, and scientists rely on approximations based upon statistical mechanics
.
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
, a radial distribution function (RDF), (or pair correlation function) g(r), describes how the atomic density varies as a function of the distance from one particular atom.
More precisely, if there is an atom at the origin O, and if n = N/V is the average number density, then the local density at distance r from O is ng(r).
Given a potential energy
Potential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
function, the radial distribution function can be found either via computer simulation methods like the Monte Carlo method
Monte Carlo method
Monte Carlo methods are a class of computational algorithms that rely on repeated random sampling to compute their results. Monte Carlo methods are often used in computer simulations of physical and mathematical systems...
, or via the Ornstein-Zernike equation, using approximative closure relations like the Perckus-Yevick approximation or the Hypernetted Chain Theory
Hypernetted-chain equation
In statistical mechanics the hypernetted-chain equation is a closure relation to solve the Ornstein–Zernike equation which relates the direct correlation function to the total correlation function. It is commonly used in fluid theory to obtain e.g. expressions for the radial distribution function...
.
Importance of g(r)
g(r) is of fundamental importance in thermodynamics because macroscopic thermodynamic quantities can be calculated using g(r). A few examples:The virial equation for the pressure:
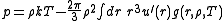
The energy equation:
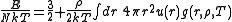
The compressibility equation
Compressibility equation
In statistical mechanics and thermodynamics the compressibility equation refers to an equation which relates the isothermal compressibility to the structure of the liquid...
:
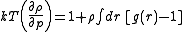
Gases
As long as the gas is dilute, the correlations in the positions of the atoms that g(r) takes into account are due to the potential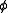 (r) that an atom at P feels owing to the presence of an atom at O. Using the Boltzmann distribution law:
(r) that an atom at P feels owing to the presence of an atom at O. Using the Boltzmann distribution law:If
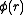 were zero for all r – i.e., if the atoms did not exert any influence on each other, then g(r) = 1 for all r. Then the mean local density would be equal to the mean density
were zero for all r – i.e., if the atoms did not exert any influence on each other, then g(r) = 1 for all r. Then the mean local density would be equal to the mean density 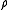 : the presence of an atom at O would not influence the presence or absence of any other atom and the gas would be ideal. As long as there is a
: the presence of an atom at O would not influence the presence or absence of any other atom and the gas would be ideal. As long as there is a 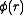 the mean local density will always be different from the mean density
the mean local density will always be different from the mean density  due to the interactions between atoms.
due to the interactions between atoms.When the density of the gas gets higher, the low-density limit is not applicable anymore because the atoms attracted to and repelled by the atom at O also repel and attract each other. The correction terms needed to correctly describe g(r) resemble the virial equation, which is an expansion in the density:
in which additional functions
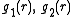 appear which may depend on temperature
appear which may depend on temperature 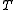 and distance
and distance  but not on density,
but not on density, 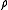 .
.Experimental
It is possible to measure g(r) experimentally with neutron scatteringNeutron scattering
Neutron scattering,the scattering of free neutrons by matter,is a physical processand an experimental technique using this processfor the investigation of materials.Neutron scattering as a physical process is of primordial importance...
or x-ray scattering diffraction data. For an example of an RDF experiment see Eigen vs. Zundel structures in HCl solution, 2006
It is additionally possible to calculate g(r) experimentally by extracting particle positions from video or confocal microscopy, as detailed in:
- Methods of Digital Video Microscopy for Colloidal Studies
- Direct Visualization of Long-Range Heterogeneous Structure in Dense Colloidal Gels
Formal derivation
Consider a system of N particles in a volume V and at a temperature T. The probability of finding atom 1 in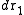 , atom 2 in
, atom 2 in 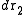 , etc., is given by
, etc., is given bywhere
 and
and 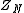 is the configurational integral. To obtain the probability of finding atom 1 in
is the configurational integral. To obtain the probability of finding atom 1 in 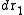 and atom n in
and atom n in 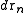 , irrespective of the remaining N − n atoms, one has to integrate (7) over the coordinates of atoms n + 1 through N:
, irrespective of the remaining N − n atoms, one has to integrate (7) over the coordinates of atoms n + 1 through N:Now the probability that any atom is in
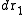 and any atom in
and any atom in 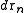 , irrespective of the rest of the atoms, is
, irrespective of the rest of the atoms, isFor n = 1 the one-particle distribution function is obtained which, for a crystal, is a periodic function with sharp maxima at the lattice sites. For a (homogeneous) liquid:
It is now time to introduce a correlation function
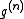 by
by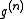 is called a correlation function, since if the atoms are independent from each other
is called a correlation function, since if the atoms are independent from each other 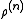 would simply equal
would simply equal 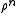 and therefore
and therefore 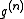 corrects for the correlation between atoms.
corrects for the correlation between atoms.From (9) it can be shown that
In the theory of liquids
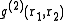 is of special importance for it can be determined experimentally using X-ray diffraction. If the liquid contains spherically symmetric atoms
is of special importance for it can be determined experimentally using X-ray diffraction. If the liquid contains spherically symmetric atoms 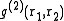 depends only on the relative distance between atoms,
depends only on the relative distance between atoms, 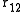 . People usually drop the subscripts:
. People usually drop the subscripts: 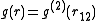 . Now
. Now 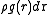 is the probability of finding an atom at r given that there is an atom at the origin of r. Note that this probability is not normalized:
is the probability of finding an atom at r given that there is an atom at the origin of r. Note that this probability is not normalized:In fact, this equation gives us the number of atoms between r and r + dr about a central atom.
Currently, information on how to obtain the higher order distribution functions
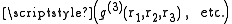 is not available, and scientists rely on approximations based upon statistical mechanics
is not available, and scientists rely on approximations based upon statistical mechanicsStatistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
.
See also
- Ornstein–Zernike equationOrnstein–Zernike equationIn statistical mechanics the Ornstein–Zernike equation is an integral equation for defining the direct correlation function. It basically describes how the correlation between two molecules can be calculated...
- Radial Distribution Function on MatDL Wiki .
- A Python script to generate Radial Distribution Function from particle coordinates stored in PDB files