Langevin equation
Encyclopedia
In statistical physics
, a Langevin equation (Paul Langevin
, 1908) is a stochastic differential equation
describing the time evolution of a subset of the degrees of freedom. These degrees of freedom typically are collective (macroscopic) variables changing only slowly in comparison to the other (microscopic) variables of the system. The fast (microscopic) variables are responsible for the stochastic nature of the Langevin equation.
, the apparently random movement of a particle in a fluid due to collisions with the molecules of the fluid,
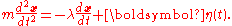
The degree of freedom of interest here is the position
of the particle, 
denotes the particle's mass. The force acting on the particle is written as a sum of a viscous force proportional to the particle's velocity (Stokes' law
), and a noise term
(the name given in physical contexts to terms in stochastic differential equations which are stochastic process
es) representing the effect of the collisions with the molecules of the fluid. The force
has a Gaussian probability distribution with correlation function
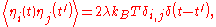
where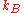
is Boltzmann's constant and T is the temperature. The δ-function of the time difference is an approximation, the actual random force has a finite correlation time corresponding to the collision time of the molecules. However, the Langevin equation is used to describe the motion of a "macroscopic" particle at a much longer time scale, and in this limit the δ-correlation and the Langevin equation become exact. Another prototypical feature of the Langevin equation is the occurrence of the damping coefficient λ in the correlation function of the random force.
An essential condition of the derivation is a criterion dividing the degrees of freedom into the categories slow and fast. For example, local thermodynamic equilibrium in a liquid is reached within a few collision times. But it takes much longer for densities of conserved quantities like mass and energy to relax to equilibrium. Densities of conserved quantities, and in particular their long wavelength components, thus are slow variable candidates. Technically this division is realized with the Zwanzig projection operator
, the essential tool in the derivation. The derivation is not completely rigorous because it relies on (plausible) assumptions akin to assumptions required elsewhere in basic statistical mechanics.
Let A={Ai} denote the slow variables. The generic Langevin equation then reads
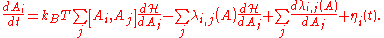
The fluctuating force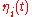
obeys a Gaussian probability distribution with correlation function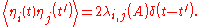
This implies the Onsager reciprocity relation
for the damping coefficients 
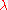. The dependence 
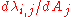of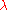 
on A is negligible in most cases.
The symbol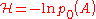
denotes the Hamiltonian of the
system, where p0(A) is the equlibribium probability distribution of the variables
. Finally, [Ai, Aj] is the Poisson bracket
of the slow variables Ai and Aj.
In the Brownian motion case one would have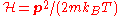
,
A={p} or A={x, p} and [xi, pj]=δi,j. The equation of motion dx/dt=p/m for x is exact, there is no fluctuating force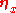
and no damping coefficient 
.
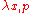One method of solution makes use of the Fokker–Planck equation, which provides a deterministic equation satisfied by the time dependent probability density. Alternatively numerical solutions can be obtained by Monte Carlo
simulation. Other techniques, such as path integrals have also been used, drawing on the analogy between statistical physics and quantum mechanics
(the Fokker-Planck equation is formally equivalent to the Schrödinger equation
).
of the time evolution of the momentum,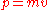
, vs. position, 
of a harmonic oscillator. Deterministic motion would follow along the ellipsoidal trajectories which cannot cross each other without changing energy. The presence of a molecular fluid environment (represented by diffusion and damping terms) continually adds and removes kinetic energy from the system, causing an initial ensemble of stochastic oscillators (dotted circles) to spread out, eventually reaching thermal equilibrium
.
R and a capacitance
C. The slow variable is the voltage U between the ends of the resistor. The Hamiltonian reads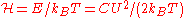
, and the Langevin equation becomes
This equation may be used to determine the correlation function
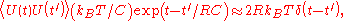
which becomes a white noise (Johnson noise) when the capacitance C becomes
negligibly small.
Statistical physics
Statistical physics is the branch of physics that uses methods of probability theory and statistics, and particularly the mathematical tools for dealing with large populations and approximations, in solving physical problems. It can describe a wide variety of fields with an inherently stochastic...
, a Langevin equation (Paul Langevin
Paul Langevin
Paul Langevin was a prominent French physicist who developed Langevin dynamics and the Langevin equation. He was one of the founders of the Comité de vigilance des intellectuels antifascistes, an antifascist organization created in the wake of the 6 February 1934 far right riots...
, 1908) is a stochastic differential equation
Stochastic differential equation
A stochastic differential equation is a differential equation in which one or more of the terms is a stochastic process, thus resulting in a solution which is itself a stochastic process....
describing the time evolution of a subset of the degrees of freedom. These degrees of freedom typically are collective (macroscopic) variables changing only slowly in comparison to the other (microscopic) variables of the system. The fast (microscopic) variables are responsible for the stochastic nature of the Langevin equation.
Brownian motion as a prototype
The original Langevin equation describes Brownian motionBrownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
, the apparently random movement of a particle in a fluid due to collisions with the molecules of the fluid,
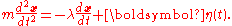
The degree of freedom of interest here is the position
of the particle, denotes the particle's mass. The force acting on the particle is written as a sum of a viscous force proportional to the particle's velocity (Stokes' lawStokes' law
In 1851, George Gabriel Stokes derived an expression, now known as Stokes' law, for the frictional force – also called drag force – exerted on spherical objects with very small Reynolds numbers in a continuous viscous fluid...
), and a noise term
Wiener process
In mathematics, the Wiener process is a continuous-time stochastic process named in honor of Norbert Wiener. It is often called standard Brownian motion, after Robert Brown...
(the name given in physical contexts to terms in stochastic differential equations which are stochastic processStochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
es) representing the effect of the collisions with the molecules of the fluid. The force
has a Gaussian probability distribution with correlation function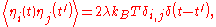where
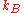is Boltzmann's constant and T is the temperature. The δ-function of the time difference is an approximation, the actual random force has a finite correlation time corresponding to the collision time of the molecules. However, the Langevin equation is used to describe the motion of a "macroscopic" particle at a much longer time scale, and in this limit the δ-correlation and the Langevin equation become exact. Another prototypical feature of the Langevin equation is the occurrence of the damping coefficient λ in the correlation function of the random force.Generic Langevin equation
There is a formal derivation of a generic Langevin equation from classical mechanics. This generic equation plays a central role in the theory of critical dynamics, and other areas of nonequilibrium statistical mechanics. The equation for Brownian motion above is a special case.An essential condition of the derivation is a criterion dividing the degrees of freedom into the categories slow and fast. For example, local thermodynamic equilibrium in a liquid is reached within a few collision times. But it takes much longer for densities of conserved quantities like mass and energy to relax to equilibrium. Densities of conserved quantities, and in particular their long wavelength components, thus are slow variable candidates. Technically this division is realized with the Zwanzig projection operator
Zwanzig projection operator
The Zwanzig projection operator is a mathematical device used in statistical mechanics.It operates in the linear space of phase space functions and projects onto the linear subspace of "slow"...
, the essential tool in the derivation. The derivation is not completely rigorous because it relies on (plausible) assumptions akin to assumptions required elsewhere in basic statistical mechanics.
Let A={Ai} denote the slow variables. The generic Langevin equation then reads
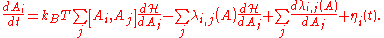
The fluctuating force
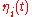obeys a Gaussian probability distribution with correlation function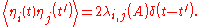This implies the Onsager reciprocity relation
Onsager reciprocal relations
In thermodynamics, the Onsager reciprocal relations express the equality of certain ratios between flows and forces in thermodynamic systems out of equilibrium, but where a notion of local equilibrium exists....
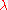for the damping coefficients . The dependence 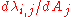of 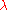on A is negligible in most cases.The symbol
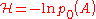denotes the Hamiltonian of thesystem, where p0(A) is the equlibribium probability distribution of the variables
. Finally, [Ai, Aj] is the Poisson bracketPoisson bracket
In mathematics and classical mechanics, the Poisson bracket is an important binary operation in Hamiltonian mechanics, playing a central role in Hamilton's equations of motion, which govern the time-evolution of a Hamiltonian dynamical system...
of the slow variables Ai and Aj.
In the Brownian motion case one would have
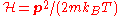,A={p} or A={x, p} and [xi, pj]=δi,j. The equation of motion dx/dt=p/m for x is exact, there is no fluctuating force
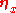and no damping coefficient 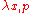.Other examples and additional notes
A solution of a Langevin equation for a particular realization of the fluctuating force is of no interest by itself, what is of interest are correlation functions of the slow variables after averaging over the fluctuating force.One method of solution makes use of the Fokker–Planck equation, which provides a deterministic equation satisfied by the time dependent probability density. Alternatively numerical solutions can be obtained by Monte Carlo
Monte Carlo method
Monte Carlo methods are a class of computational algorithms that rely on repeated random sampling to compute their results. Monte Carlo methods are often used in computer simulations of physical and mathematical systems...
simulation. Other techniques, such as path integrals have also been used, drawing on the analogy between statistical physics and quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
(the Fokker-Planck equation is formally equivalent to the Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
).
Harmonic oscillator in a fluid
The diagram at right shows a phase portraitPhase portrait
A phase portrait is a geometric representation of the trajectories of a dynamical system in the phase plane. Each set of initial conditions is representated by a different curve, or point....
of the time evolution of the momentum,
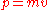, vs. position, of a harmonic oscillator. Deterministic motion would follow along the ellipsoidal trajectories which cannot cross each other without changing energy. The presence of a molecular fluid environment (represented by diffusion and damping terms) continually adds and removes kinetic energy from the system, causing an initial ensemble of stochastic oscillators (dotted circles) to spread out, eventually reaching thermal equilibriumCanonical ensemble
The canonical ensemble in statistical mechanics is a statistical ensemble representing a probability distribution of microscopic states of the system...
.
Thermal noise in an electrical resistor
Another application is Johnson noise, the electric voltage generated by thermal fluctuations in every resistor. The diagram at the right shows an electric circuit consisting of a resistanceElectrical resistance
The electrical resistance of an electrical element is the opposition to the passage of an electric current through that element; the inverse quantity is electrical conductance, the ease at which an electric current passes. Electrical resistance shares some conceptual parallels with the mechanical...
R and a capacitance
Capacitance
In electromagnetism and electronics, capacitance is the ability of a capacitor to store energy in an electric field. Capacitance is also a measure of the amount of electric potential energy stored for a given electric potential. A common form of energy storage device is a parallel-plate capacitor...
C. The slow variable is the voltage U between the ends of the resistor. The Hamiltonian reads
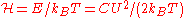, and the Langevin equation becomesThis equation may be used to determine the correlation function
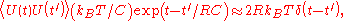
which becomes a white noise (Johnson noise) when the capacitance C becomes
negligibly small.
Further reading
- W. T. Coffey (Trinity College, DublinTrinity College, DublinTrinity College, Dublin , formally known as the College of the Holy and Undivided Trinity of Queen Elizabeth near Dublin, was founded in 1592 by letters patent from Queen Elizabeth I as the "mother of a university", Extracts from Letters Patent of Elizabeth I, 1592: "...we...found and...
, Ireland), Yu P. Kalmykov (Université de Perpignan, FranceFranceThe French Republic , The French Republic , The French Republic , (commonly known as France , is a unitary semi-presidential republic in Western Europe with several overseas territories and islands located on other continents and in the Indian, Pacific, and Atlantic oceans. Metropolitan France...
) & J. T. Waldron (Trinity College, Dublin, Ireland), The Langevin Equation, With Applications to Stochastic Problems in Physics, Chemistry and Electrical Engineering (Second Edition), World Scientific Series in Contemporary Chemical Physics - Vol 14. (The First Edition is Vol 10) - Reif, F. Fundamentals of Statistical and Thermal Physics, McGraw Hill New York, 1965. See section 15.5 Langevin Equation
- R. Friedrich, J. Peinke and Ch. Renner. How to Quantify Deterministic and Random Influences on the Statistics of the Foreign Exchange Market, Phys. Rev. Lett. 84, 5224 - 5227 (2000)
- L.C.G. Rogers and D. Williams. Diffusions, Markov Processes, and Martingales, Cambridge Mathematical Library, Cambridge University Press, Cambridge, reprint of 2nd (1994) edition, 2000.