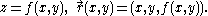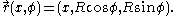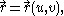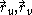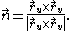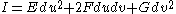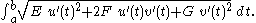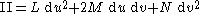Parametric surface
Encyclopedia
A parametric surface is a surface
in the Euclidean space
R3 which is defined by a parametric equation
with two parameters. Parametric representation is the most general way to specify a surface. Surfaces that occur in two of the main theorems of vector calculus, Stokes' theorem
and the divergence theorem
, are frequently given in a parametric form. The curvature and arc length
of curve
s on the surface, surface area
, differential geometric invariants such as the first
and second fundamental forms, Gaussian
, mean
, and principal
curvatures can all be computed from a given parametrization.
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
in the Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
R3 which is defined by a parametric equation
Parametric equation
In mathematics, parametric equation is a method of defining a relation using parameters. A simple kinematic example is when one uses a time parameter to determine the position, velocity, and other information about a body in motion....
with two parameters. Parametric representation is the most general way to specify a surface. Surfaces that occur in two of the main theorems of vector calculus, Stokes' theorem
Stokes' theorem
In differential geometry, Stokes' theorem is a statement about the integration of differential forms on manifolds, which both simplifies and generalizes several theorems from vector calculus. Lord Kelvin first discovered the result and communicated it to George Stokes in July 1850...
and the divergence theorem
Divergence theorem
In vector calculus, the divergence theorem, also known as Gauss' theorem , Ostrogradsky's theorem , or Gauss–Ostrogradsky theorem is a result that relates the flow of a vector field through a surface to the behavior of the vector field inside the surface.More precisely, the divergence theorem...
, are frequently given in a parametric form. The curvature and arc length
Arc length
Determining the length of an irregular arc segment is also called rectification of a curve. Historically, many methods were used for specific curves...
of curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
s on the surface, surface area
Surface area
Surface area is the measure of how much exposed area a solid object has, expressed in square units. Mathematical description of the surface area is considerably more involved than the definition of arc length of a curve. For polyhedra the surface area is the sum of the areas of its faces...
, differential geometric invariants such as the first
First fundamental form
In differential geometry, the first fundamental form is the inner product on the tangent space of a surface in three-dimensional Euclidean space which is induced canonically from the dot product of R3. It permits the calculation of curvature and metric properties of a surface such as length and...
and second fundamental forms, Gaussian
Gaussian curvature
In differential geometry, the Gaussian curvature or Gauss curvature of a point on a surface is the product of the principal curvatures, κ1 and κ2, of the given point. It is an intrinsic measure of curvature, i.e., its value depends only on how distances are measured on the surface, not on the way...
, mean
Mean curvature
In mathematics, the mean curvature H of a surface S is an extrinsic measure of curvature that comes from differential geometry and that locally describes the curvature of an embedded surface in some ambient space such as Euclidean space....
, and principal
Principal curvature
In differential geometry, the two principal curvatures at a given point of a surface are the eigenvalues of the shape operator at the point. They measure how the surface bends by different amounts in different directions at that point.-Discussion:...
curvatures can all be computed from a given parametrization.
Examples
- The simplest type of parametric surfaces is given by the graphs of functions of two variables:
- Surfaces of revolutionSurface of revolutionA surface of revolution is a surface in Euclidean space created by rotating a curve around a straight line in its plane ....
give another important class of surfaces that can be easily parametrized. If the graph z = f(x), a ≤ x ≤ b is rotated about the z-axis then the resulting surface has a parametrization
-
-
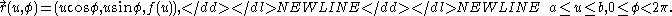
- The straight circular cylinderCylinder (geometry)A cylinder is one of the most basic curvilinear geometric shapes, the surface formed by the points at a fixed distance from a given line segment, the axis of the cylinder. The solid enclosed by this surface and by two planes perpendicular to the axis is also called a cylinder...
of radius R about x-axis has the following parametric representation:
- Using the spherical coordinates, the unit sphereSphereA sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
can be parameterized by
- This parametrization breaks down at the north and south poles where the polar angle θ is not determined uniquely.
The same surface admits many different parametrizations. For example, the coordinate z-plane can be parametrized as

for any constants a, b, c, d such that ad − bc ≠ 0, i.e. the matrix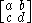 is invertible.
is invertible.
Local differential geometry
The local shape of a parametric surface can be analyzed by considering the Taylor expansion of the function that parametrizes it. The arc length of a curve on the surface and the surface area can be found using integrationIntegralIntegration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
.
Notation
Let the parametric surface be given by the equation
where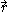 is a vector-valued functionVector-valued functionA vector-valued function also referred to as a vector function is a mathematical function of one or more variables whose range is a set of multidimensional vectors or infinite-dimensional vectors. The input of a vector-valued function could be a scalar or a vector...
is a vector-valued functionVector-valued functionA vector-valued function also referred to as a vector function is a mathematical function of one or more variables whose range is a set of multidimensional vectors or infinite-dimensional vectors. The input of a vector-valued function could be a scalar or a vector...
of the parameters (u, v) and the parameters vary within a certain domain D in the parametric uv-plane. The first partial derivatives with respect to the parameters are usually denoted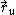 and
and 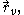 and similarly for the higher derivatives,
and similarly for the higher derivatives, 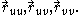
In vector calculus, the parameters are frequently denoted (s,t) and the partial derivatives are written out using the ∂-notation:
-
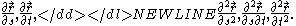
Tangent plane and normal vector
The parametrization is regular for the given values of the parameters if the vectors
are linearly independent. The tangent plane at a regular point is the affine plane in R3 spanned by these vectors and passing through the point r(u, v) on the surface determined by the parameters. Any tangent vector can be uniquely decomposed into a linear combinationLinear combinationIn mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of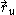 and
and  The cross productCross productIn mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
The cross productCross productIn mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
of these vectors is a normal vector to the tangent plane. Dividing this vector by its length yields a unit normal vector to the parametrised surface at a regular point:
In general, there are two choices of the unit normal vector to a surface at a given point, but for a regular parametrised surface, the preceding formula consistently picks one of them, and thus determines an orientationOrientabilityIn mathematics, orientability is a property of surfaces in Euclidean space measuring whether or not it is possible to make a consistent choice of surface normal vector at every point. A choice of surface normal allows one to use the right-hand rule to define a "clockwise" direction of loops in the...
of the surface. Some of the differential-geometric invariants of a surface in R3 are defined by the surface itself and are independent of the orientation, while others change the sign if the orientation is reversed.
Surface area
The surface areaSurface areaSurface area is the measure of how much exposed area a solid object has, expressed in square units. Mathematical description of the surface area is considerably more involved than the definition of arc length of a curve. For polyhedra the surface area is the sum of the areas of its faces...
can be calculated by integrating the length of the normal vector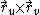 to the surface over the appropriate region D in the parametric uv plane:
to the surface over the appropriate region D in the parametric uv plane:
-

Although this formula provides a closed expression for the surface area, for all but very special surfaces this results in a complicated double integral, which is typically evaluated using a computer algebra systemComputer algebra systemA computer algebra system is a software program that facilitates symbolic mathematics. The core functionality of a CAS is manipulation of mathematical expressions in symbolic form.-Symbolic manipulations:...
or approximated numerically. Fortunately, many common surfaces form exceptions, and their areas are explicitly known. This is true for a circular cylinderCylinder (geometry)A cylinder is one of the most basic curvilinear geometric shapes, the surface formed by the points at a fixed distance from a given line segment, the axis of the cylinder. The solid enclosed by this surface and by two planes perpendicular to the axis is also called a cylinder...
, sphereSphereA sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
, coneCone (geometry)A cone is an n-dimensional geometric shape that tapers smoothly from a base to a point called the apex or vertex. Formally, it is the solid figure formed by the locus of all straight line segments that join the apex to the base...
, torusTorusIn geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
, and a few other surfaces of revolutionSurface of revolutionA surface of revolution is a surface in Euclidean space created by rotating a curve around a straight line in its plane ....
.
This can also be expressed as a surface integralSurface integralIn mathematics, a surface integral is a definite integral taken over a surface ; it can be thought of as the double integral analog of the line integral...
over the scalar field 1: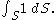
First fundamental form
The first fundamental form is a quadratic formQuadratic formIn mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
on the tangent plane to the surface which is used to calculate distances and angles. For a parametrized surface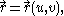 its coefficients can be computed as follows:
its coefficients can be computed as follows:
-
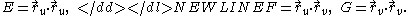
Arc lengthArc lengthDetermining the length of an irregular arc segment is also called rectification of a curve. Historically, many methods were used for specific curves...
of parametrised curves on the surface S, the angle between curves on S, and the surface area all admit expressions in terms of the first fundamental form.
If (u(t), v(t)), a ≤ t ≤ b represents a parametrised curve on this surface then its arc length can be calculated as the integral:
The first fundamental form may be viewed as a family of positive definiteDefinite bilinear formIn mathematics, a definite bilinear form is a bilinear form B over some vector space V such that the associated quadratic formQ=B \,...
symmetric bilinear formSymmetric bilinear formA symmetric bilinear form is a bilinear form on a vector space that is symmetric. Symmetric bilinear forms are of great importance in the study of orthogonal polarity and quadrics....
s on the tangent plane at each point of the surface depending smoothly on the point. This perspective helps one calculate the angle between two curves on S intersecting at a given point. This angle is equal to the angle between the tangent vectors to the curves. The first fundamental form evaluated on this pair of vectors is their dot productDot productIn mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
, and the angle can be found from the standard formula
expressing the cosine of the angle via the dot product.
Surface area can be expressed in terms of the first fundamental form as follows:
The expression under the square root is precisely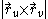 , and so it is strictly positive at the regular points.
, and so it is strictly positive at the regular points.
Second fundamental form
The second fundamental form
is a quadratic form on the tangent plane to the surface that, together with the first fundamental form, determines the curvatures of curves on the surface. In the special case when (u, v) = (x, y) and the tangent plane to the surface at the given point is horizontal, the second fundamental form is essentially the quadratic part of the Taylor expansion of z as a function of x and y.
For a general parametric surface, the definition is more complicated, but the second fundamental form depends only on the partial derivativePartial derivativeIn mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
s of order one and two.
Its coefficients are defined to be the projections of the second partial derivatives of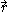 onto the unit normal vector
onto the unit normal vector 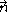 defined by the parametrization:
defined by the parametrization:
-
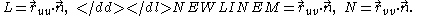
Like the first fundamental form, the second fundamental form may be viewed as a family of symmetric bilinear forms on the tangent plane at each point of the surface depending smoothly on the point.
Curvature
The first and second fundamental forms of a surface determine its important differential-geometric invariantsInvariant (mathematics)In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
: the Gaussian curvatureGaussian curvatureIn differential geometry, the Gaussian curvature or Gauss curvature of a point on a surface is the product of the principal curvatures, κ1 and κ2, of the given point. It is an intrinsic measure of curvature, i.e., its value depends only on how distances are measured on the surface, not on the way...
, the mean curvatureMean curvatureIn mathematics, the mean curvature H of a surface S is an extrinsic measure of curvature that comes from differential geometry and that locally describes the curvature of an embedded surface in some ambient space such as Euclidean space....
, and the principal curvaturePrincipal curvatureIn differential geometry, the two principal curvatures at a given point of a surface are the eigenvalues of the shape operator at the point. They measure how the surface bends by different amounts in different directions at that point.-Discussion:...
s.
The principal curvatures are the invariants of the pair consisting of the second and first fundamental forms. They are the roots κ1, κ2 of the quadratic equation
-
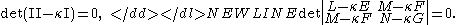
The Gaussian curvature K = κ1κ2 and the mean curvature H = 1/2(κ1 + κ2) can be computed as follows:
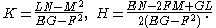
Up to a sign, these quantities are independent of the parametrization used, and hence form important tools for analysing the geometry of the surface. More precisely, the principal curvatures and the mean curvature change the sign if the orientation of the surface is reversed, and the Gaussian curvature is entirely independent of the parametrization.
The sign of the Gaussian curvature at a point determines the shape of the surface near that point: for K > 0 the surface is locally convexConvex setIn Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
and the point is called elliptic, while for K < 0 the surface is saddle shaped and the point is called hyperbolic. The points at which the Gaussian curvature is zero are called parabolic. In general, parabolic points form a curve on the surface called the parabolic line. The first fundamental form is positive definite, hence its determinant EG − F2 is positive everywhere. Therefore, the sign of K coincides with the sign of LN − M2, the determinant of the second fundamental
External links
-
-
-
-
- The straight circular cylinder
-