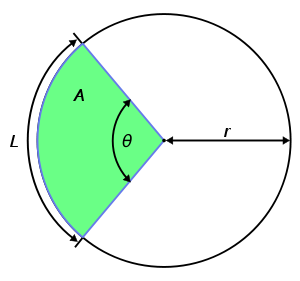
In geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, an arc is a closed

Closed set

In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...

 segment of a differentiable curve

Curve

In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...

 in the two-dimensional plane; for example, a circular arc is a segment of the circumference

Circumference

The circumference is the distance around a closed curve. Circumference is a special perimeter.-Circumference of a circle:The circumference of a circle is the length around it....

 of a circle. If the arc is part of a great circle

Great circle

A great circle, also known as a Riemannian circle, of a sphere is the intersection of the sphere and a plane which passes through the center point of the sphere, as opposed to a general circle of a sphere where the plane is not required to pass through the center...

 (or great ellipse

Great ellipse

left|150px|thumb|A [[spheroid]].A great ellipse is an ellipse passing through two points on a spheroid and having the same center as that of the spheroid. Equivalently,it is an ellipse on the surface of a cylinder centered at the origin....

), it is called a great arc.

Arc length

The length

Arc length

Determining the length of an irregular arc segment is also called rectification of a curve. Historically, many methods were used for specific curves...

 of an arc of a circle with radius and subtending an angle (measured in radian

Radian

Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...

s) with the circle center — i.e., the central angle

Central angle

A central angle is an angle which vertex is the center of a circle, and whose sides pass through a pair of points on the circle, thereby subtending an arc between those two points whose angle is equal to the central angle itself...

— equals 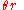. This is because


Substituting in the circumference


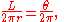
and solving for arc length, 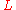, in terms of yields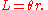


An angle of degrees has a size in radians given by


and so the arc length equals


A practical way to determine the length of an arc in a circle is to plot two lines from the arc's endpoints to the center of the circle, measure the angle where the two lines meet the center, then solve for L by cross-multiplying the statement:

measure of angle

Angle

In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...

/360 = L/Circumference.

For example, if the measure of the angle is 60 degrees and the Circumference is 24", then

60/360 = L/24

360L=1440

L = 4".

This is so because the circumference of a circle and the degrees of a circle, of which there are always 360, are directly proportionate.

Arc area

The area between an arc and the center of a circle is:


The area has the same proportion to the circle area as the angle 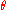to a full circle: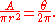


We can get rid of a on both sides:


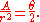
By multiplying both sides by 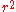, we get the final result:


Using the conversion described above, we find that the area of the sector for a central angle measured in degrees is:

Arc segment area

The area of the shape limited by the arc and a straight line between the two end points is: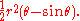


To get the area of the arc segment, we need to subtract the area of the triangle made up by the circle's center and the two end points of the arc from the area . See Circular segment

Circular segment

In geometry, a circular segment is an area of a circle informally defined as an area which is "cut off" from the rest of the circle by a secant or a chord. The circle segment constitutes the part between the secant and an arc, excluding the circle's center...

 for details.

Arc radius

Using the equality in the intersecting chords theorem (also known as power of a point

Power of a point

In elementary plane geometry, the power of a point is a real number h that reflects the relative distance of a given point from a given circle. Specifically, the power of a point P with respect to a circle C of radius r is defined...

 or secant tangent theorem) it is possible to calculate the radius of a circle given the height and the width of an arc using: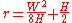

See also

• Arc length
  Arc length
  Determining the length of an irregular arc segment is also called rectification of a curve. Historically, many methods were used for specific curves...
  
  
• Circular-arc graph
  Circular-arc graph
  In graph theory, a circular-arc graph is the intersection graph of a set of arcs on the circle. It has one vertex for each arc in the set, and an edge between every pair of vertices corresponding to arcs that intersect....
  
  
• Meridian arc
  Meridian arc
  In geodesy, a meridian arc measurement is a highly accurate determination of the distance between two points with the same longitude. Two or more such determinations at different locations then specify the shape of the reference ellipsoid which best approximates the shape of the geoid. This...
  
  
• Other meanings of arc

Similar shapes:

• Catenary
  Catenary
  In physics and geometry, the catenary is the curve that an idealised hanging chain or cable assumes when supported at its ends and acted on only by its own weight. The curve is the graph of the hyperbolic cosine function, and has a U-like shape, superficially similar in appearance to a parabola...
  
  

External links

• Definition and properties of a circular arc With interactive animation
• A collection of pages defining arcs and their properties, with animated applets Arcs, arc central angle, arc peripheral angle, central angle theorem and others.
• Radius of an arc or segment With interactive animation