Differential geometry of curves
Encyclopedia
Differential geometry of curves is the branch of geometry
that deals
with smooth curve
s in the plane and in the Euclidean space
by methods of differential
and integral calculus.
Starting in antiquity, many concrete curves have been thoroughly investigated using the synthetic approach. Differential geometry takes another path: curves are represented in a parametrized form
, and their geometric properties and various quantities associated with them, such as the curvature
and the arc length
, are expressed via derivative
s and integral
s using vector calculus. One of the most important tools used to analyze a curve is the Frenet frame, a moving frame that provides a coordinate system at each point of the curve that is "best adapted" to the curve near that point.
The theory of curves is much simpler and narrower in scope than the theory of surfaces
and its higher-dimensional generalizations, because a regular curve in a Euclidean space has no intrinsic geometry. Any regular curve may be parametrized by the arc length (the natural parametrization) and from the point of view of a bug on the curve that does not know anything about the ambient space, all curves would appear the same. Different space curves are only distinguished by the way in which they bend and twist. Quantitatively, this is measured by the differential-geometric invariants called the curvature
and the torsion
of a curve. The fundamental theorem of curves
asserts that the knowledge of these invariants completely determines the curve.

of class Cr (i.e. γ is r times continuously differentiable
) is called a parametric curve of class Cr or a Cr parametrization of the curve γ. t is called the parameter
of the curve γ. γ(I) is called the image of the curve. It is important to distinguish between a curve γ and the image of a curve γ(I) because a given image can be described by several different Cr curves.
One may think of the parameter t as representing time and the curve γ(t) as the trajectory
of a moving particle in space.
If I is a closed interval [a, b], we call γ(a) the starting point and γ(b) the endpoint of the curve γ.
If γ(a) = γ(b), we say γ is closed or a loop. Furthermore, we call γ a closed Cr-curve if γ(k)(a) = γ(k)(b) for all k ≤ r.
If γ:(a,b) → Rn is injective, we call the curve simple.
If γ is a parametric curve which can be locally described as a power series, we call the curve analytic or of class .
.
We write -γ to say the curve is traversed in opposite direction.
A Ck-curve

is called regular of order m if for any t in interval I

are linearly independent
in Rn.
In particular, a C1-curve γ is regular if
 for any
for any  .
.
on the set of all parametric curves. The differential geometric properties of a curve (length, frenet frame and generalized curvature) are invariant under reparametrization and therefore properties of the equivalence class.The equivalence classes are called Cr curves and are central objects studied in the differential geometry of curves.
Two parametric curves of class Cr

and

are said to be equivalent if there exists a bijective Cr map

such that

and

γ2 is said to be a reparametrisation of γ1. This reparametrisation of γ1 defines the equivalence relation on the set of all parametric Cr curves. The equivalence class is called a Cr curve.
We can define an even finer equivalence relation of oriented Cr curves by requiring φ to be φ‘(t) > 0.
Equivalent Cr curves have the same image. And equivalent oriented Cr curves even traverse the image in the same direction.

The length of a curve is invariant under reparametrization and therefore a differential geometric property of the curve.
For each regular Cr-curve (r at least 1) γ: [a, b] → Rn we can define a function

Writing

where t(s) is the inverse of s(t), we get a reparametrization of γ which is called natural, arc-length or unit speed parametrization. The parameter s(t) is called the natural parameter of γ.
of γ which is called natural, arc-length or unit speed parametrization. The parameter s(t) is called the natural parameter of γ.
We prefer this parametrization because the natural parameter s(t) traverses the image of γ at unit speed so that

In practice it is often very difficult to calculate the natural parametrization of a curve, but it is useful for theoretical arguments.
For a given parametrized curve γ(t) the natural parametrization is unique up to shift of parameter.
The quantity

is sometimes called the energy or action
of the curve; this name is justified because the geodesic
equations are the Euler–Lagrange equations of motion for this action.
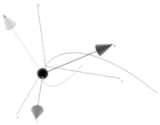
 A Frenet frame is a moving reference frame
A Frenet frame is a moving reference frame
of n orthonormal vectors ei(t) which are used to describe a curve locally at each point γ(t). It is the main tool in the differential geometric treatment of curves as it is far easier and more natural to describe local properties (e.g. curvature, torsion) in terms of a local reference system than using a global one like the Euclidean coordinates.
Given a Cn+1-curve γ in Rn which is regular of order n the Frenet frame for the curve is the set of orthonormal vectors

called Frenet vectors. They are constructed from the derivatives of γ(t) using the Gram–Schmidt orthogonalization algorithm
with


The real-valued functions χi(t) are called generalized curvatures and are defined as

The Frenet frame and the generalized curvatures are invariant under reparametrization and are therefore differential geometric properties of the curve.
of the particle at a given point P is expressed by a vector, called the tangent vector to the curve at P. Mathematically, given a parametrized C1 curve γ = γ(t), for every value t = t0 of the parameter, the vector
is the tangent vector at the point P = γ(t0). Generally speaking, the tangent vector may be zero. The magnitude of the tangent vector,

is the speed at the time t0.
The first Frenet vector e1(t) is the unit tangent vector in the same direction, defined at each regular point of γ:

If t = s is the natural parameter then the tangent vector has unit length, so that the formula simplifies:

The unit tangent vector determines the orientation of the curve, or the forward direction, corresponding to the increasing values of the parameter. The unit tangent vector taken as a curve traces the spherical image
of the original curve.
It is defined as
Its normalized form, the unit normal vector, is the second Frenet vector e2(t) and defined as

The tangent and the normal vector at point t define the osculating plane
at point t.

and is called the curvature
of γ at point t.
The reciprocal
of the curvature

is called the radius of curvature.
A circle with radius r has a constant curvature of
whereas a line has a curvature of 0.
It is always orthogonal to the unit tangent and normal vectors at t, and is defined as

In 3-dimensional space the equation simplifies to

and is called the torsion of γ at point t.

with

then there exists a unique (up to transformations using the Euclidean group
) Cn+1-curve γ which is regular of order n and has the following properties


where the set

is the Frenet frame for the curve.
By additionally providing a start t0 in I, a starting point p0 in Rn and an initial positive orthonormal Frenet frame {e1, ..., en-1} with


we can eliminate the Euclidean transformations and get unique curve γ.
\begin{bmatrix}
0 & -\kappa(t) \\
\kappa(t) & 0 \\
\end{bmatrix}
\begin{bmatrix}
\mathbf{e}_1(t)\\
\mathbf{e}_2(t) \\
\end{bmatrix}


Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
that deals
with smooth curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
s in the plane and in the Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
by methods of differential
Differential calculus
In mathematics, differential calculus is a subfield of calculus concerned with the study of the rates at which quantities change. It is one of the two traditional divisions of calculus, the other being integral calculus....
and integral calculus.
Starting in antiquity, many concrete curves have been thoroughly investigated using the synthetic approach. Differential geometry takes another path: curves are represented in a parametrized form
Parametric equation
In mathematics, parametric equation is a method of defining a relation using parameters. A simple kinematic example is when one uses a time parameter to determine the position, velocity, and other information about a body in motion....
, and their geometric properties and various quantities associated with them, such as the curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
and the arc length
Arc length
Determining the length of an irregular arc segment is also called rectification of a curve. Historically, many methods were used for specific curves...
, are expressed via derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
s and integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
s using vector calculus. One of the most important tools used to analyze a curve is the Frenet frame, a moving frame that provides a coordinate system at each point of the curve that is "best adapted" to the curve near that point.
The theory of curves is much simpler and narrower in scope than the theory of surfaces
Differential geometry of surfaces
In mathematics, the differential geometry of surfaces deals with smooth surfaces with various additional structures, most often, a Riemannian metric....
and its higher-dimensional generalizations, because a regular curve in a Euclidean space has no intrinsic geometry. Any regular curve may be parametrized by the arc length (the natural parametrization) and from the point of view of a bug on the curve that does not know anything about the ambient space, all curves would appear the same. Different space curves are only distinguished by the way in which they bend and twist. Quantitatively, this is measured by the differential-geometric invariants called the curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
and the torsion
Torsion of curves
In the elementary differential geometry of curves in three dimensions, the torsion of a curve measures how sharply it is twisting. Taken together,the curvature and the torsion of a space curve are analogous to the curvature of a plane curve...
of a curve. The fundamental theorem of curves
Fundamental theorem of curves
In differential geometry, the fundamental theorem of curves states that any regular curve with non-zero curvature has its shape completely determined by its curvature and torsion....
asserts that the knowledge of these invariants completely determines the curve.
Definitions
Let n be a natural number, r a natural number or ∞, I be a non-empty interval of real numbers and t in I. A vector-valued functionVector-valued function
A vector-valued function also referred to as a vector function is a mathematical function of one or more variables whose range is a set of multidimensional vectors or infinite-dimensional vectors. The input of a vector-valued function could be a scalar or a vector...

of class Cr (i.e. γ is r times continuously differentiable
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
) is called a parametric curve of class Cr or a Cr parametrization of the curve γ. t is called the parameter
Parameter
Parameter from Ancient Greek παρά also “para” meaning “beside, subsidiary” and μέτρον also “metron” meaning “measure”, can be interpreted in mathematics, logic, linguistics, environmental science and other disciplines....
of the curve γ. γ(I) is called the image of the curve. It is important to distinguish between a curve γ and the image of a curve γ(I) because a given image can be described by several different Cr curves.
One may think of the parameter t as representing time and the curve γ(t) as the trajectory
Trajectory
A trajectory is the path that a moving object follows through space as a function of time. The object might be a projectile or a satellite, for example. It thus includes the meaning of orbit—the path of a planet, an asteroid or a comet as it travels around a central mass...
of a moving particle in space.
If I is a closed interval [a, b], we call γ(a) the starting point and γ(b) the endpoint of the curve γ.
If γ(a) = γ(b), we say γ is closed or a loop. Furthermore, we call γ a closed Cr-curve if γ(k)(a) = γ(k)(b) for all k ≤ r.
If γ:(a,b) → Rn is injective, we call the curve simple.
If γ is a parametric curve which can be locally described as a power series, we call the curve analytic or of class
 .
.We write -γ to say the curve is traversed in opposite direction.
A Ck-curve

is called regular of order m if for any t in interval I

are linearly independent
Linear independence
In linear algebra, a family of vectors is linearly independent if none of them can be written as a linear combination of finitely many other vectors in the collection. A family of vectors which is not linearly independent is called linearly dependent...
in Rn.
In particular, a C1-curve γ is regular if
 for any
for any  .
.Reparametrization and equivalence relation
Given the image of a curve one can define several different parameterizations of the curve. Differential geometry aims to describe properties of curves invariant under certain reparametrizations. So we have to define a suitable equivalence relationEquivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
on the set of all parametric curves. The differential geometric properties of a curve (length, frenet frame and generalized curvature) are invariant under reparametrization and therefore properties of the equivalence class.The equivalence classes are called Cr curves and are central objects studied in the differential geometry of curves.
Two parametric curves of class Cr

and

are said to be equivalent if there exists a bijective Cr map

such that

and

γ2 is said to be a reparametrisation of γ1. This reparametrisation of γ1 defines the equivalence relation on the set of all parametric Cr curves. The equivalence class is called a Cr curve.
We can define an even finer equivalence relation of oriented Cr curves by requiring φ to be φ‘(t) > 0.
Equivalent Cr curves have the same image. And equivalent oriented Cr curves even traverse the image in the same direction.
Length and natural parametrization
The length l of a curve γ : [a, b] → Rn of class C1 can be defined as
The length of a curve is invariant under reparametrization and therefore a differential geometric property of the curve.
For each regular Cr-curve (r at least 1) γ: [a, b] → Rn we can define a function

Writing

where t(s) is the inverse of s(t), we get a reparametrization
 of γ which is called natural, arc-length or unit speed parametrization. The parameter s(t) is called the natural parameter of γ.
of γ which is called natural, arc-length or unit speed parametrization. The parameter s(t) is called the natural parameter of γ.We prefer this parametrization because the natural parameter s(t) traverses the image of γ at unit speed so that

In practice it is often very difficult to calculate the natural parametrization of a curve, but it is useful for theoretical arguments.
For a given parametrized curve γ(t) the natural parametrization is unique up to shift of parameter.
The quantity

is sometimes called the energy or action
Action (physics)
In physics, action is an attribute of the dynamics of a physical system. It is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Action has the dimension of energy × time, and its unit is...
of the curve; this name is justified because the geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
equations are the Euler–Lagrange equations of motion for this action.
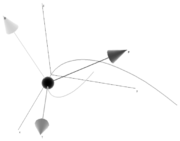
Frenet frame

Moving frame
In mathematics, a moving frame is a flexible generalization of the notion of an ordered basis of a vector space often used to study the extrinsic differential geometry of smooth manifolds embedded in a homogeneous space.-Introduction:...
of n orthonormal vectors ei(t) which are used to describe a curve locally at each point γ(t). It is the main tool in the differential geometric treatment of curves as it is far easier and more natural to describe local properties (e.g. curvature, torsion) in terms of a local reference system than using a global one like the Euclidean coordinates.
Given a Cn+1-curve γ in Rn which is regular of order n the Frenet frame for the curve is the set of orthonormal vectors

called Frenet vectors. They are constructed from the derivatives of γ(t) using the Gram–Schmidt orthogonalization algorithm
Gram–Schmidt process
In mathematics, particularly linear algebra and numerical analysis, the Gram–Schmidt process is a method for orthonormalising a set of vectors in an inner product space, most commonly the Euclidean space Rn...
with


The real-valued functions χi(t) are called generalized curvatures and are defined as

The Frenet frame and the generalized curvatures are invariant under reparametrization and are therefore differential geometric properties of the curve.
Special Frenet vectors and generalized curvatures
The first three Frenet vectors and generalized curvatures can be visualized in three-dimensional space. They have additional names and more semantic information attached to them.Tangent vector
If a curve γ represents the path of a particle then the instantaneous velocityVelocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
of the particle at a given point P is expressed by a vector, called the tangent vector to the curve at P. Mathematically, given a parametrized C1 curve γ = γ(t), for every value t = t0 of the parameter, the vector
-
 at
at 
is the tangent vector at the point P = γ(t0). Generally speaking, the tangent vector may be zero. The magnitude of the tangent vector,

is the speed at the time t0.
The first Frenet vector e1(t) is the unit tangent vector in the same direction, defined at each regular point of γ:

If t = s is the natural parameter then the tangent vector has unit length, so that the formula simplifies:

The unit tangent vector determines the orientation of the curve, or the forward direction, corresponding to the increasing values of the parameter. The unit tangent vector taken as a curve traces the spherical image
Spherical image
In differential geometry, the spherical image of a unit-speed curve is given by taking the curve's tangent vectors as points, all of which must lie on the unit sphere...
of the original curve.
Normal or curvature vector
The normal vector, sometimes called the curvature vector, indicates the deviance of the curve from being a straight line.It is defined as

Its normalized form, the unit normal vector, is the second Frenet vector e2(t) and defined as

The tangent and the normal vector at point t define the osculating plane
Osculating plane
In mathematics, particularly in differential geometry, an osculating plane is a plane in a Euclidean space or affine space which meets a submanifold at a point in such a way as to have a second order of contact at the point. The word osculate is from the Latin osculatus which is a past participle...
at point t.
Curvature
The first generalized curvature χ1(t) is called curvature and measures the deviance of γ from being a straight line relative to the osculating plane. It is defined as
and is called the curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
of γ at point t.
The reciprocal
Multiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
of the curvature

is called the radius of curvature.
A circle with radius r has a constant curvature of

whereas a line has a curvature of 0.
Binormal vector
The binormal vector is the third Frenet vector e3(t).It is always orthogonal to the unit tangent and normal vectors at t, and is defined as

In 3-dimensional space the equation simplifies to

Torsion
The second generalized curvature χ2(t) is called torsion and measures the deviance of γ from being a plane curve. Or, in other words, if the torsion is zero, the curve lies completely in the same osculating plane (there is only one osculating plane for every point t). It is defined as
and is called the torsion of γ at point t.
Main theorem of curve theory
Given n functions
with

then there exists a unique (up to transformations using the Euclidean group
Euclidean group
In mathematics, the Euclidean group E, sometimes called ISO or similar, is the symmetry group of n-dimensional Euclidean space...
) Cn+1-curve γ which is regular of order n and has the following properties


where the set

is the Frenet frame for the curve.
By additionally providing a start t0 in I, a starting point p0 in Rn and an initial positive orthonormal Frenet frame {e1, ..., en-1} with


we can eliminate the Euclidean transformations and get unique curve γ.
Frenet–Serret formulas
The Frenet–Serret formulas are a set of ordinary differential equations of first order. The solution is the set of Frenet vectors describing the curve specified by the generalized curvature functions χi\begin{bmatrix}
0 & -\kappa(t) \\
\kappa(t) & 0 \\
\end{bmatrix}
\begin{bmatrix}
\mathbf{e}_1(t)\\
\mathbf{e}_2(t) \\
\end{bmatrix}
3 dimensions

n dimensions (general formula)

Additional reading
- Erwin Kreyszig, Differential Geometry, Dover Publications, New York, 1991, ISBN 9780484667218. Chapter II is a classical treatment of Theory of Curves in 3-dimensions.

