
Curve sketching
Encyclopedia
In geometry
, curve sketching (or curve tracing) includes techniques that can used to produce a rough idea of overall shape of a plane curve
given its equation without computing the large numbers of points required for a detailed plot. It is an application of the theory of curves to find their main features.
) is a technique for determining the shape of an algebraic curve close to and far away from the origin. It consists of plotting (α, β) for each term Axαyβ in the equation of the curve. The resulting diagram is then analyzed to produce information about the curve.
Specifically, draw a diagonal line connecting two points on the diagram so that every other point is either on or to the right and above it. There is at least one such line if the curve passes through the origin. Let the equation of the line be qα+pβ=r. Suppose the curve is approximated by y=Cxp/q near the origin. Then the term Axαyβ is approximately Dxα+βp/q. The exponent is r/q when (α, β) is on the line and higher when it is above and to the right. Therefore, the significant terms near the origin under this assumption are only those lying on the line and the others may be ignored it produce a simple approximate equation for the curve. There may be several such diagonal lines, each corresponding to one or more branches of the curve, and the approximate equations of the branches may be found by applying this method to each line in turn.
For example, the folium of Descartes
is defined by the equation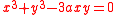 .
.
Then Newton's diagram has points at (3, 0), (1, 1), and (0, 3). Two diagonal lines may be drawn as described above, 2α+β=3 and α+2β=3. These produce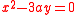
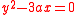
as approximate equations for the horizontal and vertical branches of the curve where they cross at the origin.
extended Newton's diagram to form a technique called the analytical triangle (or de Gua's triangle). The points (α, β) are plotted as with Newton's diagram method but the line α+β=n, where n is the degree of the curve, is added to form a triangle which contains the diagram. This method considers all lines which bound the smallest convex polygon which contains the plotted points (see convex hull
).
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, curve sketching (or curve tracing) includes techniques that can used to produce a rough idea of overall shape of a plane curve
Plane curve
In mathematics, a plane curve is a curve in a Euclidean plane . The most frequently studied cases are smooth plane curves , and algebraic plane curves....
given its equation without computing the large numbers of points required for a detailed plot. It is an application of the theory of curves to find their main features.
Basic techniques
The following are usually easy to carry out and give important clues as to the shape of a curve:- Determine the x and y intercepts of the curve. The x intercepts are found by setting y equal to 0 in the equation of the curve and solving for x. Similarly, the y intercepts are found by setting x equal to 0 in the equation of the curve and solving for y
- Determine the symmetry of the curve. If the exponent of x is always even in the equation of the curve then the y-axis is an axis of symmetryReflection symmetryReflection symmetry, reflectional symmetry, line symmetry, mirror symmetry, mirror-image symmetry, or bilateral symmetry is symmetry with respect to reflection. That is, a figure which does not change upon undergoing a reflection has reflectional symmetry.In 2D there is a line of symmetry, in 3D a...
for the curve. Similarly, if the exponent of y is always even in the equation of the curve then the x-axis is an axis of symmetry for the curve. If the sum of the degrees of x and y in each term is always even or always odd, then the curve is symmetric about the originRotational symmetryGenerally speaking, an object with rotational symmetry is an object that looks the same after a certain amount of rotation. An object may have more than one rotational symmetry; for instance, if reflections or turning it over are not counted, the triskelion appearing on the Isle of Man's flag has...
and the origin is called a center of the curve. - Determine any bounds on the values of x and y.
- If the curve passes through the origin then determine the tangent lines there. For algebraic curves, this can be done by removing all but the terms of lowest order from the equation and solving.
- Similarly, removing all but the terms of highest order from the equation and solving gives the points where the curve meets the line at infinityLine at infinityIn geometry and topology, the line at infinity is a line that is added to the real plane in order to give closure to, and remove the exceptional cases from, the incidence properties of the resulting projective plane. The line at infinity is also called the ideal line.-Geometric formulation:In...
. - Determine the asymptoteAsymptoteIn analytic geometry, an asymptote of a curve is a line such that the distance between the curve and the line approaches zero as they tend to infinity. Some sources include the requirement that the curve may not cross the line infinitely often, but this is unusual for modern authors...
s of the curve. Also determine from which side the curve approaches the asymptotes and where the asymptotes intersect the curve.
Newton's diagram
Newton's diagram (also known as Newton's parallelogram, after Isaac NewtonIsaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
) is a technique for determining the shape of an algebraic curve close to and far away from the origin. It consists of plotting (α, β) for each term Axαyβ in the equation of the curve. The resulting diagram is then analyzed to produce information about the curve.
Specifically, draw a diagonal line connecting two points on the diagram so that every other point is either on or to the right and above it. There is at least one such line if the curve passes through the origin. Let the equation of the line be qα+pβ=r. Suppose the curve is approximated by y=Cxp/q near the origin. Then the term Axαyβ is approximately Dxα+βp/q. The exponent is r/q when (α, β) is on the line and higher when it is above and to the right. Therefore, the significant terms near the origin under this assumption are only those lying on the line and the others may be ignored it produce a simple approximate equation for the curve. There may be several such diagonal lines, each corresponding to one or more branches of the curve, and the approximate equations of the branches may be found by applying this method to each line in turn.
For example, the folium of Descartes
Folium of Descartes
In geometry, the Folium of Descartes is an algebraic curve defined by the equationx^3 + y^3 - 3 a x y = 0 \,.It forms a loop in the first quadrant with a double point at the origin and asymptotex + y + a = 0 \,.It is symmetrical about y = x....
is defined by the equation
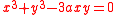 .
.Then Newton's diagram has points at (3, 0), (1, 1), and (0, 3). Two diagonal lines may be drawn as described above, 2α+β=3 and α+2β=3. These produce
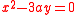
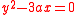
as approximate equations for the horizontal and vertical branches of the curve where they cross at the origin.
The analytical triangle
de GuaJean Paul de Gua de Malves
Jean Paul de Gua de Malves was a French mathematician who published in 1740 a work on analytical geometry in which he applied it, without the aid of differential calculus, to find the tangents, asymptotes, and various singular points of an algebraic curve.He further showed how singular points and...
extended Newton's diagram to form a technique called the analytical triangle (or de Gua's triangle). The points (α, β) are plotted as with Newton's diagram method but the line α+β=n, where n is the degree of the curve, is added to form a triangle which contains the diagram. This method considers all lines which bound the smallest convex polygon which contains the plotted points (see convex hull
Convex hull
In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
).

