
Position vector
Encyclopedia
In geometry
, a position, location, or radius vector, usually denoted , is a vector which represents the position of a point P in space in relation to an arbitrary reference origin
, is a vector which represents the position of a point P in space in relation to an arbitrary reference origin
O. It corresponds to the displacement
from O to P:
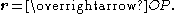
The concept typically applies to two-
or three-dimensional space
, but can be easily generalized to Euclidean space
s with a higher number of dimension
s.

Acceleration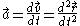
Jolt/Jerk/Surge/Lurch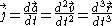
Snap/Jounce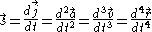
Crackle/Trounce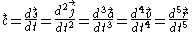
Pop/Pounce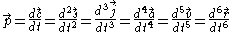
Lock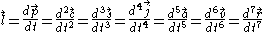
Drop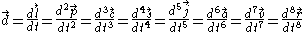
Where is the position vector,
is the position vector, 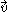 is the velocity vector,
is the velocity vector, 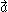 is the acceleration vector,
is the acceleration vector, 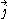 is the jerk vector,
is the jerk vector, 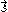 is the snap vector,
is the snap vector, 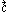 is the crackle vector,
is the crackle vector, 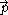 is the pop vector,
is the pop vector, 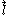 is the lock vector, and
is the lock vector, and 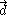 is the drop vector.
is the drop vector.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a position, location, or radius vector, usually denoted
 , is a vector which represents the position of a point P in space in relation to an arbitrary reference origin
, is a vector which represents the position of a point P in space in relation to an arbitrary reference originOrigin (mathematics)
In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...
O. It corresponds to the displacement
Displacement (vector)
A displacement is the shortest distance from the initial to the final position of a point P. Thus, it is the length of an imaginary straight path, typically distinct from the path actually travelled by P...
from O to P:
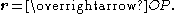
The concept typically applies to two-
Two-dimensional space
- Details :Bi-dimensional space is a geometric model of the planar projection of the physical universe in which we live.The two dimensions are commonly called length and width .Both directions lies in the same plane....
or three-dimensional space
Three-dimensional space
Three-dimensional space is a geometric 3-parameters model of the physical universe in which we live. These three dimensions are commonly called length, width, and depth , although any three directions can be chosen, provided that they do not lie in the same plane.In physics and mathematics, a...
, but can be easily generalized to Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
s with a higher number of dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
s.
Applications
- In linear algebraLinear algebraLinear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, a position vector can be expressed as a linear combination of basis vectors.
- The kinematicKinematicsKinematics is the branch of classical mechanics that describes the motion of bodies and systems without consideration of the forces that cause the motion....
movement of a point mass can be described by a vector-valued functionVector-valued functionA vector-valued function also referred to as a vector function is a mathematical function of one or more variables whose range is a set of multidimensional vectors or infinite-dimensional vectors. The input of a vector-valued function could be a scalar or a vector...
giving the position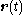 as a function of the scalar time parameter t. These are used in mechanics and dynamics to keep track of the positions of particles, point masses, or rigid objects.
as a function of the scalar time parameter t. These are used in mechanics and dynamics to keep track of the positions of particles, point masses, or rigid objects.
- In differential geometry, position vector fields are used to describe continuous and differentiable space curves, in which case the independent parameter needs not be time, but can be (e.g.) arc length of the curve.
Derivatives of Position
Velocity
Acceleration
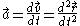
Jolt/Jerk/Surge/Lurch
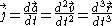
Snap/Jounce
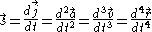
Crackle/Trounce
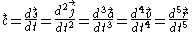
Pop/Pounce
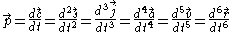
Lock
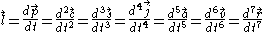
Drop
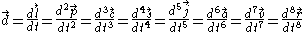
Where
 is the position vector,
is the position vector, 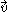 is the velocity vector,
is the velocity vector, 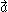 is the acceleration vector,
is the acceleration vector, 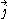 is the jerk vector,
is the jerk vector, 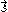 is the snap vector,
is the snap vector, 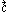 is the crackle vector,
is the crackle vector, 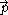 is the pop vector,
is the pop vector, 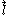 is the lock vector, and
is the lock vector, and 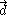 is the drop vector.
is the drop vector.
