
Line segment
Encyclopedia

Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a line segment is a part of a line
Line (mathematics)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
that is bounded by two end points
Point (geometry)
In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon
Polygon
In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
, the line segment is either an edge
Edge (geometry)
In geometry, an edge is a one-dimensional line segment joining two adjacent zero-dimensional vertices in a polygon. Thus applied, an edge is a connector for a one-dimensional line segment and two zero-dimensional objects....
(of that polygon) if they are adjacent vertices, or otherwise a diagonal
Diagonal
A diagonal is a line joining two nonconsecutive vertices of a polygon or polyhedron. Informally, any sloping line is called diagonal. The word "diagonal" derives from the Greek διαγώνιος , from dia- and gonia ; it was used by both Strabo and Euclid to refer to a line connecting two vertices of a...
. When the end points both lie on a curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
such as a circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
, a line segment is called a chord
Chord (geometry)
A chord of a circle is a geometric line segment whose endpoints both lie on the circumference of the circle.A secant or a secant line is the line extension of a chord. More generally, a chord is a line segment joining two points on any curve, such as but not limited to an ellipse...
(of that curve).
Definition
If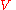 is a vector space
is a vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
over
 or
or  , and
, and 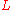 is a subset
is a subsetSubset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of
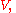 then
then 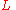 is a line segment if
is a line segment if  can be parameterized as
can be parameterized as
for some vectors
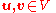 , in which case the vectors
, in which case the vectors  and
and  are called the end points of
are called the end points of 
Sometimes one needs to distinguish between "open" and "closed" line segments. Then one defines a closed line segment as above, and an open line segment as a subset
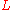 that can be parametrized as
that can be parametrized as
for some vectors
 .
.Equivalently, a line segment is the convex hull
Convex hull
In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
of two points. Thus, the line segment can be expressed as a convex combination
Convex combination
In convex geometry, a convex combination is a linear combination of points where all coefficients are non-negative and sum up to 1....
of the segment's two end points.
In geometry, it is sometimes defined that a point B is between two other points A and C, if the distance AB added to the distance BC is equal to the distance AC. Thus the equation of a line segment with endpoints A =
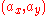 and C =
and C =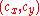 is
is
Properties
- A line segment is a connected, non-empty set.
- If
 is a topological vector spaceTopological vector spaceIn mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
is a topological vector spaceTopological vector spaceIn mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
, then a closed line segment is a closed setClosed setIn geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
in However, an open line segment is an open set in
However, an open line segment is an open set in  if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
 is one-dimensional.
is one-dimensional. - More generally than above, the concept of a line segment can be defined in an ordered geometryOrdered geometryOrdered geometry is a form of geometry featuring the concept of intermediacy but, like projective geometry, omitting the basic notion of measurement...
.
In proofs
In an axiomatic treatment of Geometry, the notion of betweenness is either assumed to satisfy a certain number of axioms, or else defined in terms of an isometry of a line (used as a coordinate system).Segments play an important role in other theories. For example, a set is convex if the segment that joins any two points of the set is contained in the set. This is important because it transforms some of the analysis of convex sets to the analysis of a line segment.
As a degenerate ellipse
A line segment can be viewed as a degenerate caseDegenerate conic
In mathematics, a degenerate conic is a conic that fails to be an irreducible curve...
of an ellipse
Ellipse
In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
in which the semiminor axis goes to zero, the foci
Focus (geometry)
In geometry, the foci are a pair of special points with reference to which any of a variety of curves is constructed. For example, foci can be used in defining conic sections, the four types of which are the circle, ellipse, parabola, and hyperbola...
go to the end points, and the eccentricity goes to one. As a degenerate orbit this is a radial elliptic trajectory.
See also
- Interval (mathematics)Interval (mathematics)In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
- Line (geometry)Line (geometry)The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
- Line segment intersectionLine segment intersectionIn computational geometry, the line segment intersection problem supplies a list of line segments in the plane and asks us to determine whether any two of them intersect, or cross....
, the algorithmic problem of finding intersecting pairs in a collection of line segments - SpirangleSpirangleSpirangles are geometric figures related to spirals. They are similar to spirals in that they expand from a center point as they grow larger, but they are made out of straight line segments, instead of curves...
External links
- http://planetmath.org/encyclopedia/LineSegment.htmlLine Segment at PlanetMathPlanetMathPlanetMath is a free, collaborative, online mathematics encyclopedia. The emphasis is on rigour, openness, pedagogy, real-time content, interlinked content, and also community of about 24,000 people with various maths interests. Intended to be comprehensive, the project is hosted by the Digital...
] - Definition of line segment With interactive animation
- Copying a line segment with compass and straightedge
- Dividing a line segment into N equal parts with compass and straightedge Animated demonstration
----

