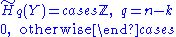Jordan curve theorem
Encyclopedia

Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, a Jordan curve is a non-self-intersecting continuous loop
Loop (topology)
In mathematics, a loop in a topological space X is a path f from the unit interval I = [0,1] to X such that f = f...
in the plane, and another name for a Jordan curve is a "simple closed curve". The Jordan curve theorem asserts that every Jordan curve divides the plane into an "interior" region bounded by the curve and an "exterior" region containing all of the nearby and far away exterior points, so that any continuous path
Path (topology)
In mathematics, a path in a topological space X is a continuous map f from the unit interval I = [0,1] to XThe initial point of the path is f and the terminal point is f. One often speaks of a "path from x to y" where x and y are the initial and terminal points of the path...
connecting a point of one region to a point of the other intersects with that loop somewhere. While the statement of this theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
seems to be intuitively obvious, it takes quite a bit of ingenuity to prove it by elementary means. More transparent proofs rely on the mathematical machinery of algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, and these lead to generalizations to higher-dimensional spaces.
The Jordan curve theorem is named after the mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Camille Jordan
Camille Jordan
Marie Ennemond Camille Jordan was a French mathematician, known both for his foundational work in group theory and for his influential Cours d'analyse. He was born in Lyon and educated at the École polytechnique...
, who found its first proof. For decades, it was generally thought that this proof was flawed and that the first rigorous proof was carried out by Oswald Veblen
Oswald Veblen
Oswald Veblen was an American mathematician, geometer and topologist, whose work found application in atomic physics and the theory of relativity. He proved the Jordan curve theorem in 1905.-Life:...
. However, this notion has been challenged by Thomas C. Hales
Thomas Callister Hales
Thomas Callister Hales is an American mathematician. He is known for his 1998 computer-aided proof of the Kepler conjecture, a centuries-old problem in discrete geometry which states that the most space-efficient way to pack spheres is in a pyramid shape...
and others.
Definitions and the statement of the Jordan theorem
A Jordan curve or a simple closed curve in the plane R2 is the imageImage (mathematics)
In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
C of an injective continuous map of a circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
into the plane, φ: S1 → R2.
A Jordan arc in the plane is the image of an injective continuous map of a closed interval into the plane.
Alternatively, a Jordan curve is the image of a continuous map φ: [0,1] → R2 such that φ(0) = φ(1) and the restriction of φ to [0,1) is injective. The first two conditions say that C is a continuous loop, whereas the last condition stipulates that C has no self-intersection points.
Let C be a Jordan curve in the plane R2. Then its complementComplement (set theory)In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
, R2 \ C, consists of exactly two connected components. One of these components is boundedBounded setIn mathematical analysis and related areas of mathematics, a set is called bounded, if it is, in a certain sense, of finite size. Conversely, a set which is not bounded is called unbounded...
(the interior) and the other is unbounded (the exterior), and the curve C is the boundaryBoundary (topology)In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
of each component.
Furthermore, the complement of a Jordan arc in the plane is connected.
Proof and generalizations
The Jordan curve theorem was independently generalized to higher dimensions by H. Lebesgue and L.E.J. Brouwer in 1911, resulting in the Jordan–Brouwer separation theorem.
Let X be a topological sphere in the (n+1)-dimensional Euclidean spaceEuclidean spaceIn mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn+1, i.e. the image of an injective continuous mapping of the n-sphere Sn into Rn+1. Then the complement Y of X in Rn+1 consists of exactly two connected components. One of these components is bounded (the interior) and the other is unbounded (the exterior). The set X is their common boundary.
The proof uses homology theory
Homology theory
In mathematics, homology theory is the axiomatic study of the intuitive geometric idea of homology of cycles on topological spaces. It can be broadly defined as the study of homology theories on topological spaces.-The general idea:...
. It is first established that, more generally, if X is homeomorphic to the k-sphere, then the reduced integral homology
Reduced homology
In mathematics, reduced homology is a minor modification made to homology theory in algebraic topology, designed to make a point have all its homology groups zero...
groups of Y = Rn+1 \ X are as follows:
This is proved by induction in k using the Mayer–Vietoris sequence. When n = k, the zeroth reduced homology of Y has rank 1, which means that Y has 2 connected components (which are, moreover, path connected), and with a bit of extra work, one shows that their common boundary is X. A further generalization was found by J.W. Alexander, who established the Alexander duality
Alexander duality
In mathematics, Alexander duality refers to a duality theory presaged by a result of 1915 by J. W. Alexander, and subsequently further developed, particularly by P. S. Alexandrov and Lev Pontryagin...
between the reduced homology of a compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
subset X of Rn+1 and the reduced cohomology of its complement. If X is an n-dimensional compact connected submanifold of Rn+1 (or Sn+1) without boundary, its complement has 2 connected components.
There is a strengthening of the Jordan curve theorem, called the Jordan–Schönflies theorem, which states that the interior and the exterior planar regions determined by a Jordan curve in R2 are homeomorphic to the interior and exterior of the unit disk. In particular, for any point P in the interior region and a point A on the Jordan curve, there exists a Jordan arc connecting P with A and, with the exception of the endpoint A, completely lying in the interior region. An alternative and equivalent formulation of the Jordan–Schönflies theorem asserts that any Jordan curve φ: S1 → R2, where S1 is viewed as the unit circle
Unit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
in the plane, can be extended to a homeomorphism ψ: R2 → R2 of the plane. Unlike Lebesgues' and Brouwer's generalization of the Jordan curve theorem, this statement becomes false in higher dimensions: while the exterior of the unit ball in R3 is simply connected, because it retracts
Deformation retract
In topology, a branch of mathematics, a retraction , as the name suggests, "retracts" an entire space into a subspace. A deformation retraction is a map which captures the idea of continuously shrinking a space into a subspace.- Retract :...
onto the unit sphere, the Alexander horned sphere
Alexander horned sphere
The Alexander horned sphere is a wild embedding of a sphere into space, discovered by . It is the particular embedding of a sphere in 3-dimensional Euclidean space obtained by the following construction, starting with a standard torus:...
is a subset of R3 homeomorphic to a sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
, but so twisted in space that the unbounded component of its complement in R3 is not simply connected, and hence not homeomorphic to the exterior of the unit ball.
History and further proofs
The statement of the Jordan curve theorem may seem obvious at first, but it is a rather difficult theorem to prove. Bernard BolzanoBernard Bolzano
Bernhard Placidus Johann Nepomuk Bolzano , Bernard Bolzano in English, was a Bohemian mathematician, logician, philosopher, theologian, Catholic priest and antimilitarist of German mother tongue.-Family:Bolzano was the son of two pious Catholics...
was the first man to formulate a precise conjecture, observing that it was not a self-evident statement, but that it required a proof. It is easy to establish this result for polygonal lines, but the problem came in generalizing it to all kinds of badly behaved curves, which include nowhere differentiable curves, such as the Koch snowflake
Koch snowflake
The Koch snowflake is a mathematical curve and one of the earliest fractal curves to have been described...
and other fractal curves, or even a Jordan curve of positive area
Osgood curve
In mathematics, an Osgood curve is a Jordan curve of positive area. The first example was found by .Examples of Osgood curves can be produced by slightly modifying one of the constructions of space-filling curves with image the unit square to make it an embedding, though the cost is that it no...
constructed by .
The first proof was of this theorem given by Camille Jordan
Camille Jordan
Marie Ennemond Camille Jordan was a French mathematician, known both for his foundational work in group theory and for his influential Cours d'analyse. He was born in Lyon and educated at the École polytechnique...
in his lectures on real analysis
Real analysis
Real analysis, is a branch of mathematical analysis dealing with the set of real numbers and functions of a real variable. In particular, it deals with the analytic properties of real functions and sequences, including convergence and limits of sequences of real numbers, the calculus of the real...
, and it published in his book Cours d'analyse de l'École Polytechnique. There is some controversy about whether Jordan's proof was complete: the majority of commenters on it have claimed that the first complete proof was later given by Oswald Veblen
Oswald Veblen
Oswald Veblen was an American mathematician, geometer and topologist, whose work found application in atomic physics and the theory of relativity. He proved the Jordan curve theorem in 1905.-Life:...
, who said the following about Jordan's proof:
However, Thomas C. Hales
Thomas Callister Hales
Thomas Callister Hales is an American mathematician. He is known for his 1998 computer-aided proof of the Kepler conjecture, a centuries-old problem in discrete geometry which states that the most space-efficient way to pack spheres is in a pyramid shape...
wrote:
Hales also pointed out that the special case of simple polygons is not only an easy exercise, but was not really used by Jordan anyway, and quoted Reeken as saying:
Jordan's proof and another early proof by de la Vallée-Poussin were later critically analyzed and completed by Shoenflies (1924).
Due to the importance of the Jordan curve theorem in low-dimensional topology
Low-dimensional topology
In mathematics, low-dimensional topology is the branch of topology that studies manifolds of four or fewer dimensions. Representative topics are the structure theory of 3-manifolds and 4-manifolds, knot theory, and braid groups. It can be regarded as a part of geometric topology.A number of...
and complex analysis
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, it received much attention from prominent mathematicians of the first half of the [20th century]]. Various proofs of the theorem and its generalizations were constructed by J. W. Alexander
James Waddell Alexander II
James Waddell Alexander II was a mathematician and topologist of the pre-World War II era and part of an influential Princeton topology elite, which included Oswald Veblen, Solomon Lefschetz, and others...
, Louis Antoine
Louis Antoine
Louis Antoine was a French mathematician who discovered Antoine's necklace, which J. W. Alexander used to construct Antoine's horned sphere....
, Bieberbach, Luitzen Brouwer, Denjoy, Hartogs, Kerékjártó, Alfred Pringsheim
Alfred Pringsheim
Alfred Israel Pringsheim was a German mathematician and patron of the arts. He was born in Ohlau, Prussian Silesia and died in Zürich, Switzerland.- Family and academic career :...
, and Schoenflies.
Some new elementary proofs of the Jordan curve theorem, as well as simplifications of the earlier proofs, continue to be carried out.
- A proof using the Brouwer fixed point theoremBrouwer fixed point theoremBrouwer's fixed-point theorem is a fixed-point theorem in topology, named after Luitzen Brouwer. It states that for any continuous function f with certain properties there is a point x0 such that f = x0. The simplest form of Brouwer's theorem is for continuous functions f from a disk D to...
by . - A proof using non-standard mathematics by .
- A proof using constructive mathematics by .
- A proof using non-planarityPlanar graphIn graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
of the complete bipartite graphComplete bipartite graphIn the mathematical field of graph theory, a complete bipartite graph or biclique is a special kind of bipartite graph where every vertex of the first set is connected to every vertex of the second set.- Definition :...
K3,3 was given by . - A simplification of the proof by Helge TverbergHelge TverbergHelge Arnulf Tverberg is a Norwegian mathematician. He was a professor in the Mathematics Department at the University of Bergen, his speciality being combinatorics; he retired at the mandatory age of seventy....
.
The first formal proof
Formal proof
A formal proof or derivation is a finite sequence of sentences each of which is an axiom or follows from the preceding sentences in the sequence by a rule of inference. The last sentence in the sequence is a theorem of a formal system...
of the Jordan curve theorem was created by in the HOL Light system, in January 2005, and ot contained about 60,000 lines. Another rigorous 6,500-line formal proof was produced in 2005 by an international team of mathematicians using the Mizar system
Mizar system
The Mizar system consists of a language for writing strictly formalized mathematical definitions and proofs, a computer program which is able to check proofs written in this language, and a library of definitions and proved theorems which can be referenced and used in new articles. Mizar has goals...
. Both the Mizar and the HOL Light proof rely on libraries of previously proved theorems, so these two sizes are not comparable. showed that the Jordan curve theorem is equivalent in proof-theoretic strength to the weak König's lemma.
See also
- Lakes of WadaLakes of WadaIn mathematics, the lakes of Wada are three disjoint connected open sets of the plane with the counterintuitive property that they all have the same boundary....
- Quasi-Fuchsian groupQuasi-Fuchsian groupIn the mathematical theory of Kleinian groups, a quasi-Fuchsian group is a Kleinian group whose limit set is contained in an invariant Jordan curve. If the limit set is equal to the Jordan curve the quasi-Fuchsian group is said to be of type one, and otherwise it is said to be of type two...
, a mathematical group that preserves a Jordan curve - Complex analysisComplex analysisComplex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
External links
- The full 6,500 line formal proof of Jordan's curve theorem in MizarMizar systemThe Mizar system consists of a language for writing strictly formalized mathematical definitions and proofs, a computer program which is able to check proofs written in this language, and a library of definitions and proved theorems which can be referenced and used in new articles. Mizar has goals...
. - Collection of proofs of the Jordan curve theorem at Andrew Ranicki's homepage
- A simple proof of Jordan curve theorem (PDF) by David B. Gauld
- Application of the theorem in computer science - Determining If A Point Lies On The Interior Of A Polygon by Paul Bourke