
Spiric section
Encyclopedia
In geometry
, a spiric section, sometimes called a spiric of Perseus, is a quartic plane curve
defined by equations of the form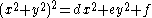 .
.
Equivalently, spiric sections can be defined as bicircular
quartic curves that are symmetric with respect to the x and y-axes. Spiric sections are included in the family of toric section
s and include the family of hippopede
s and the family of Cassini oval
s. The name is from σπειρα meaning torus in ancient Greek.
A spiric section is sometimes defined as the curve of intersection of a torus
and a plane parallel to its rotational symmetry axis. However, this definition does not include all of the curves given by the previous definition unless imaginary
planes are allowed.
Spiric sections were first described by the ancient Greek geometer Perseus
in roughly 150 BC
, and are assumed to be the first toric sections to be described.
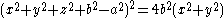 .
.
Interchanging y and z so that the axis of revolution is now on the xy-plane, and setting z=c to find the curve of intersection gives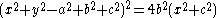 .
.
In this formula, the torus
is formed by rotating a circle of radius a with its center following another circle of radius b (not necessarily larger than a, self-intersection is permitted). The parameter c is the distance from the intersecting plane to the axis of revolution. There are no spiric sections with c > b + a, since there is no intersection; the plane is too far away from the torus to intersect it.
Expanding the equation gives the form seen in the definition
where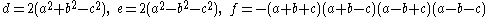 .
.
In polar coordinates this becomes
or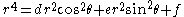 .
.
and the Cassini oval
and their relatives, such as the lemniscate of Bernoulli
. The Cassini oval
has the remarkable property that the product of distances to two foci are constant. For comparison, the sum is constant in ellipse
s, the difference is constant in hyperbola
e and the ratio is constant in circle
s.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a spiric section, sometimes called a spiric of Perseus, is a quartic plane curve
Plane curve
In mathematics, a plane curve is a curve in a Euclidean plane . The most frequently studied cases are smooth plane curves , and algebraic plane curves....
defined by equations of the form
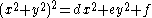 .
.Equivalently, spiric sections can be defined as bicircular
Circular algebraic curve
In geometry, a circular algebraic curve is a type of plane algebraic curve determined by an equation F = 0, where F is a polynomial with real coefficients and the highest-order terms of F form a polynomial divisible by x2 + y2...
quartic curves that are symmetric with respect to the x and y-axes. Spiric sections are included in the family of toric section
Toric section
A toric section is an intersection of a plane with a torus, just as a conic section is the intersection of a plane with a cone.-Mathematical formulae:In general, toric sections are fourth-order plane curves of the form...
s and include the family of hippopede
Hippopede
In geometry, a hippopede is a plane curve determined by an equation of the form^2=cx^2+dy^2,...
s and the family of Cassini oval
Cassini oval
A Cassini oval is a plane curve defined as the set of points in the plane such that the product of the distances to two fixed points is constant. This is related to an ellipse, for which the...
s. The name is from σπειρα meaning torus in ancient Greek.
A spiric section is sometimes defined as the curve of intersection of a torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
and a plane parallel to its rotational symmetry axis. However, this definition does not include all of the curves given by the previous definition unless imaginary
Imaginary number
An imaginary number is any number whose square is a real number less than zero. When any real number is squared, the result is never negative, but the square of an imaginary number is always negative...
planes are allowed.
Spiric sections were first described by the ancient Greek geometer Perseus
Perseus (geometer)
Perseus was an ancient Greek geometer, who invented the concept of spiric sections, in analogy to the conic sections studied by Apollonius of Perga....
in roughly 150 BC
150 BC
Year 150 BC was a year of the pre-Julian Roman calendar. At the time it was known as the Year of the Consulship of Flamininus and Balbus...
, and are assumed to be the first toric sections to be described.
Equations
Start with the usual equation for the torus: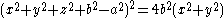 .
.Interchanging y and z so that the axis of revolution is now on the xy-plane, and setting z=c to find the curve of intersection gives
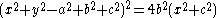 .
.In this formula, the torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
is formed by rotating a circle of radius a with its center following another circle of radius b (not necessarily larger than a, self-intersection is permitted). The parameter c is the distance from the intersecting plane to the axis of revolution. There are no spiric sections with c > b + a, since there is no intersection; the plane is too far away from the torus to intersect it.
Expanding the equation gives the form seen in the definition

where
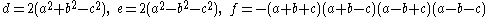 .
.In polar coordinates this becomes

or
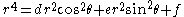 .
.Examples of spiric sections
Examples include the hippopedeHippopede
In geometry, a hippopede is a plane curve determined by an equation of the form^2=cx^2+dy^2,...
and the Cassini oval
Cassini oval
A Cassini oval is a plane curve defined as the set of points in the plane such that the product of the distances to two fixed points is constant. This is related to an ellipse, for which the...
and their relatives, such as the lemniscate of Bernoulli
Lemniscate of Bernoulli
In geometry, the lemniscate of Bernoulli is a plane curve defined from two given points F1 and F2, known as foci, at distance 2a from each other as the locus of points P so that PF1·PF2 = a2. The curve has a shape similar to the numeral 8 and to the ∞ symbol. Its name is from lemniscus, which is...
. The Cassini oval
Cassini oval
A Cassini oval is a plane curve defined as the set of points in the plane such that the product of the distances to two fixed points is constant. This is related to an ellipse, for which the...
has the remarkable property that the product of distances to two foci are constant. For comparison, the sum is constant in ellipse
Ellipse
In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
s, the difference is constant in hyperbola
Hyperbola
In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
e and the ratio is constant in circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
s.

