Catenary
Encyclopedia
In physics
and geometry
, the catenary is the curve that an idealised hanging chain
or cable
assumes when supported at its ends and acted on only by its own weight. The curve is the graph of the hyperbolic cosine function, and has a U-like shape, superficially similar in appearance to a parabola
(though mathematically quite different). Its surface of revolution
, the catenoid
, is a minimal surface
and is the shape assumed by a soap film bounded by two parallel circular rings.
". Thomas Jefferson
is usually credited with the English word catenary.
This occurs in a passage in a letter to Thomas Paine
on the construction of an arch for a bridge.
It is often stated that Galileo
thought that the curve followed by a hanging chain is a parabola.
A careful reading of his book Two new sciences shows this to be an oversimplification. Galileo states that a hanging cord is approximated by a parabola, correctly observing that this approximation improves as the curvature gets smaller and is almost exact when the elevation is less than 45°. That the curve followed by a chain is not a parabola was proven by Joachim Jungius
(1587–1657) and published posthumously in 1669.
The application of the catenary to the construction of arches is due to Robert Hooke
, who discovered it in the context of the rebuilding of St Paul's Cathedral
, possibly having seen Huygens' work on the catenary. (Some much older arches are also approximate catenaries.)
In 1671, Hooke announced to the Royal Society
that he had solved the problem of the optimal shape of an arch, and in 1675 published an encrypted solution as a Latin anagram
in an appendix to his Description of Helioscopes,
where he wrote that he had found "a true mathematical and mechanical form of all manner of Arches for Building." He did not publish the solution of this anagram in his lifetime, but in 1705 his executor provided it as Ut pendet continuum flexile, sic stabit contiguum rigidum inversum, meaning "As hangs a flexible cable so, inverted, stand the touching pieces of an arch."
In 1691 Gottfried Leibniz
, Christiaan Huygens, and Johann Bernoulli
derived the equation
in response to a challenge by Jakob Bernoulli. David Gregory wrote a treatise on the catenary in 1697.
Euler proved in 1744 that the catenary is the curve which, when rotated about the x-axis, gives the surface of minimum surface area
(the catenoid
) for the given bounding circles. Nicolas Fuss
gave equations describing the equilibrium of a chain under any force in 1796.
.jpg)
Catenary arches are often used in the construction of kiln
s. In this construction technique, the shape of a hanging chain of the desired dimensions is transferred to a form which is then used as a guide for the placement of bricks or other building material.
The Gateway Arch
in St. Louis, Missouri
, United States
is sometimes said to be an (inverted) catenary, but this is incorrect. It is close to a more general curve called a flattened catenary, with equation y=Acosh(Bx). (A catenary would have AB=1.) While a catenary is the ideal shape for a freestanding arch of constant thickness, the Gateway Arch is narrower near the top. According to the U.S. National Historic Landmark
nomination for the arch, it is a "weighted catenary" instead. Its shape corresponds to the shape that a weighted chain, having lighter links in the middle, would form.
In free-hanging chains the force exerted is uniform with respect to length of the chain and so the chain follows the catenary curve. The same is true of a simple suspension bridge
or "catenary bridge," where the roadway follows the cable.
.jpg)
A stressed ribbon bridge
is a more sophisticated structure with the same catenary shape.
However in a suspension bridge
with a suspended roadway, the chains or cables support the weight of the bridge, and so do not hang freely. In most cases the roadway is flat, so when the weight of the cable is negligible compared with the weight being supported, the force exerted is uniform with respect to horizontal distance, and the result is a parabola, as discussed below (although the term "catenary" is often still used, in an informal sense). If the cable is heavy then the resulting curve is between a catenary and a parabola.
s, and other marine assets which must be anchored to the seabed.
When the rode is slack, the catenary curve presents a lower angle of pull on the anchor
or mooring device than would be the case if it was nearly straight. This assists the performance of the anchor and raises the level of force it will resist before dragging. To maintain the catenary shape in the presence of wind, a heavy chain is needed, so that only larger ships in deeper water can rely on this effect – smaller boats must rely on the performance of the anchor itself.
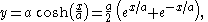
where cosh is the hyperbolic cosine function
.
The Whewell equation
for the catenary is
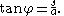
Differentiating gives
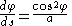
and eliminating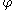
gives the Cesàro equation
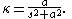
The radius of curvature
is then
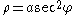
which is the length of the line normal to the curve between it and the x-axis.
to each other. Changing the parameter a is equivalent to a uniform scaling of the curve.
A parabola rolled along a straight line traces out a catenary (see roulette
) with its focus
.
Square wheel
s can roll perfectly smoothly if the road has evenly spaced bumps in the shape of a series of inverted catenary curves. The wheels can be any regular polygon except a triangle, but the catenary must have parameters corresponding to the shape and dimensions of the wheels.
A charge
in a uniform electric field
moves along a catenary (which tends to a parabola
if the charge velocity is much less than the speed of light
c).
The surface of revolution
with fixed radii at either end that has minimum surface area is a catenary revolved about the x-axis.
Over any horizontal interval, the ratio of the area under the caternary to its length equals a, independent of the interval selected. The catenary is the only plane curve other than a horizontal line with this property. Also, the geometric centroid of the area under a stretch of catenary is the midpoint of the perpendicular segment connecting the centroid of the curve itself and the x-axis.
and that it is so flexible any force exerted by the chain itself is parallel to the chain. The analysis of the curve for an optimal arch is similar except that the forces of tension become forces of compression and everything is inverted.
An underlying principle is that the chain may be considered a rigid body once it has attained equilibrium. Equations which define the shape of the curve and the tension of the chain at each point may be derived by a careful inspection of the various forces acting on a segment using the fact that these forces must be in balance if the chain is in static equilibrium.
Let the path followed by the chain is given parametrically by
r = (x, y) = (x(s), y(s)) where s represents arc length
and r is the position vector. This is the natural parameterization and has the property that
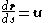
where u is a unit tangent vector.
A differential equation
for the curve may be derived as follows. Let c be the lowest point on the chain, called the vertex of the catenary,
and measure the parameter s from c. Assume r is to the right of c since the other case is implied by symmetry. The forces acting on section of the chain from c to r are the tension of the chain at c, the tension of the chain at r and the weight of the chain. The tension at c is tangent to the curve at c and is therefore horizontal, and it pulls the section to the left so it may be written (−T0, 0) where T0 is the magnitude of the force. The tension at r is parallel to the curve at r and pulls the section to the right, so it may be written Tu=(Tcos φ, Tsin φ), where T is the magnitude of the force and φ is the is the angle between the curve at r and the x-axis (see tangential angle
). Finally, weight of the chain is represented by (0, −λgs) where λ is the mass per unit length and g is the acceleration of gravity.
The chain is in equilibrium so the sum of three forces is 0, therefore
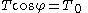
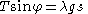
and dividing these
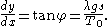
It is convenient to write
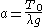
which is the length of chain whose weight is equal in magnitude to the tension at c. Then
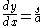
is an equation defining the curve.
It is immediate that the horizontal component of the tension, Tcos φ = λga is constant and the vertical component of the tension, Tsin φ = λgs is proportional to the length of chain between the r and the vertex.
From
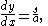
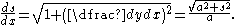
Then
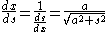
and
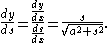
The second of these equations can be integrated to give
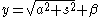
and by shifting the position of the x-axis, β can be taken to be 0. Then
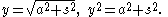
The x-axis thus chosen is called the directrix of the catenary.
It follows that the magnitude of the tension at a point T = λgy which is proportional to the distance between the point and the directrix.
The integral of expression for dx/ds can be found using standard techniques giving
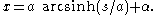
and, again, by shifting the position of the y-axis, α can be taken to be 0. Then
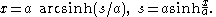
The y-axis thus chosen passes though the vertex and is called the axis of the catenary.
These results can be used to eliminate s giving
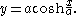
From
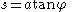
it follows
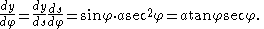
Integrating,
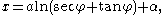
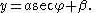
As before, the x and y-axes can be shifted so α and β can be taken to be 0. Then
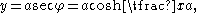
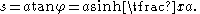
Relabel if necessary so that A is to the left of A′ and let h and k be the vertical and horizontal distances from A to A′. Translate the axes so that the origin is at the vertex of the catenary so the equation of the curve is
and let the coordinates of A and A′ be (b, c) and (b′, c′) respectively. The curve passes through these points, so
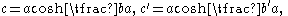
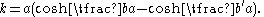
The lengths of the curve from the vertex to A and from the vertex to A′ are
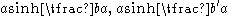
respectively, so the length from A to A′ is
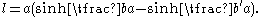
Then
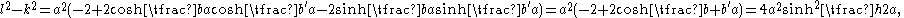
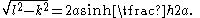
This is a transcendental equation in a and must be solved numerically. However, it can be shown with the methods of calculus that there is at most one solution with a>0 and so there is at most one position of equilibrium. Furthermore, a solution exists only when
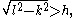
in other words l is greater than the distance from A to A′. That is, a solution exists only when the length of the chain is longer than the distance between the two points.
Let w denote the weight per unit length of the chain, then the weight of the chain has magnitude
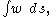
where the limits of integration are c and r. Balancing forces as before produces
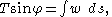
Differentiation gives
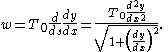
In terms of φ and the radius of curvature ρ this becomes
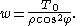
A similar analysis can be done to find the curve followed by the cable supporting a suspension bridge
with a horizontal roadway. If the weight of the roadway per unit length is w and the weight of the cable and the wire supporting the bridge is negligible in comparison, then the weight on the cable from c to r is wx where x is the horizontal distance between c to r. Proceeding a before gives the differential equation
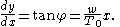
This is solved by simple integration to get
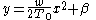
and so the cable follows a parabola. If weight of the cable and supporting wires are not negligible then the analysis is more difficult.
In this case the equations for tension are
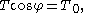
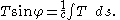
Combining gives
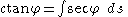
and by differentiation
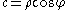
where ρ is the radius of curvature.
The solution to this is
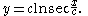
In this case, the curve has vertical asymptotes and this limits the span to πc. Other relations are
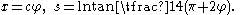
The curve was studied 1826 by Davies Gilbert
and, apparently independently, by Gaspard-Gustave Coriolis
in 1836.
catenary, the chain is replaced by a spring which can stretch in response to tension. The spring is assumed to stretch in accordance with Hooke's Law
. Specifically, if p is the natural length of a section of spring, then the length of the spring with tension T applied has length
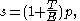
where E is a constant. In the catenary the value of T is variable, but ratio remains valid at a local level, so
The curve followed by an elastic spring can now be derived following a similar method as for the inelastic spring.
The equations for tension of the spring are
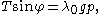
from which
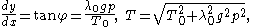
where p is the natural length of the segment from c to r and λ0 is the mass per unit length of the spring with no tension and g is the acceleration of gravity. Write
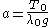
so
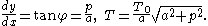
Parametric equations for the curve are now given by
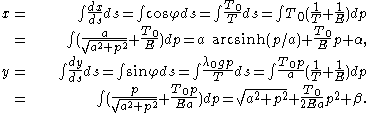
Again, the x and y-axes can be shifted so α and β can be taken to be 0. So
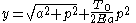
are parametric equations for the curve.
First, let T=T(s) be the force of tension as a function of s. The chain is flexible so it can only exert a force parallel to itself. Since tension is defined as the force that the chain exerts on itself, T must be parallel to the chain. In other words,
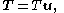
where T is the magnitude of T and u is the unit tangent vector.
Second, let G=G(s) be the external force per unit length acting on a small segment of a chain as a function of s. The forces acting on the segment of the chain between s and s+Δs are the force of tension T(s+Δs) at one end of the segment, the nearly opposite force −T(s) at the other end, and the external force acting on the segment which is
approximately GΔs. These forces must balance so
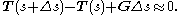
Divide by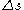
and take the limit as 
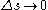to obtain
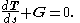
These equations can be used as the starting point in the analysis of a flexible chain acting under any external force. In the case of the standard catenary, G = (0, −λg) where the chain has mass λ per unit length and g is the acceleration of gravity.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
and geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the catenary is the curve that an idealised hanging chain
Chain
A chain is a sequence of connected links.Chain may also refer to:Chain may refer to:* Necklace - a jewelry which is worn around the neck* Mail , a type of armor made of interlocking chain links...
or cable
Cable
A cable is two or more wires running side by side and bonded, twisted or braided together to form a single assembly. In mechanics cables, otherwise known as wire ropes, are used for lifting, hauling and towing or conveying force through tension. In electrical engineering cables are used to carry...
assumes when supported at its ends and acted on only by its own weight. The curve is the graph of the hyperbolic cosine function, and has a U-like shape, superficially similar in appearance to a parabola
Parabola
In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
(though mathematically quite different). Its surface of revolution
Surface of revolution
A surface of revolution is a surface in Euclidean space created by rotating a curve around a straight line in its plane ....
, the catenoid
Catenoid
A catenoid is a three-dimensional surface made by rotating a catenary curve about its directrix. Not counting the plane, it is the first minimal surface to be discovered. It was found and proved to be minimal by Leonhard Euler in 1744. Early work on the subject was published also by Jean Baptiste...
, is a minimal surface
Minimal surface
In mathematics, a minimal surface is a surface with a mean curvature of zero.These include, but are not limited to, surfaces of minimum area subject to various constraints....
and is the shape assumed by a soap film bounded by two parallel circular rings.
History
The word catenary is derived from the Latin word catena, which means "chainChain
A chain is a sequence of connected links.Chain may also refer to:Chain may refer to:* Necklace - a jewelry which is worn around the neck* Mail , a type of armor made of interlocking chain links...
". Thomas Jefferson
Thomas Jefferson
Thomas Jefferson was the principal author of the United States Declaration of Independence and the Statute of Virginia for Religious Freedom , the third President of the United States and founder of the University of Virginia...
is usually credited with the English word catenary.
This occurs in a passage in a letter to Thomas Paine
Thomas Paine
Thomas "Tom" Paine was an English author, pamphleteer, radical, inventor, intellectual, revolutionary, and one of the Founding Fathers of the United States...
on the construction of an arch for a bridge.
I have lately received from Italy a treatise on the equilibrium of arches, by the Abbé Mascheroni. It appears to be a very scientifical work. I have not yet had time to engage in it; but I find that the conclusions of his demonstrations are, that every part of the catenary is in perfect equilibrium.The curve is also called the "alysoid", "chainette", or, particularly in the material sciences, "funicular".
It is often stated that Galileo
Galileo Galilei
Galileo Galilei , was an Italian physicist, mathematician, astronomer, and philosopher who played a major role in the Scientific Revolution. His achievements include improvements to the telescope and consequent astronomical observations and support for Copernicanism...
thought that the curve followed by a hanging chain is a parabola.
A careful reading of his book Two new sciences shows this to be an oversimplification. Galileo states that a hanging cord is approximated by a parabola, correctly observing that this approximation improves as the curvature gets smaller and is almost exact when the elevation is less than 45°. That the curve followed by a chain is not a parabola was proven by Joachim Jungius
Joachim Jungius
Joachim Jungius was a German mathematician, logician and philosopher of sciences.-Life:He was a native of Lübeck...
(1587–1657) and published posthumously in 1669.
The application of the catenary to the construction of arches is due to Robert Hooke
Robert Hooke
Robert Hooke FRS was an English natural philosopher, architect and polymath.His adult life comprised three distinct periods: as a scientific inquirer lacking money; achieving great wealth and standing through his reputation for hard work and scrupulous honesty following the great fire of 1666, but...
, who discovered it in the context of the rebuilding of St Paul's Cathedral
St Paul's Cathedral
St Paul's Cathedral, London, is a Church of England cathedral and seat of the Bishop of London. Its dedication to Paul the Apostle dates back to the original church on this site, founded in AD 604. St Paul's sits at the top of Ludgate Hill, the highest point in the City of London, and is the mother...
, possibly having seen Huygens' work on the catenary. (Some much older arches are also approximate catenaries.)
In 1671, Hooke announced to the Royal Society
Royal Society
The Royal Society of London for Improving Natural Knowledge, known simply as the Royal Society, is a learned society for science, and is possibly the oldest such society in existence. Founded in November 1660, it was granted a Royal Charter by King Charles II as the "Royal Society of London"...
that he had solved the problem of the optimal shape of an arch, and in 1675 published an encrypted solution as a Latin anagram
Anagram
An anagram is a type of word play, the result of rearranging the letters of a word or phrase to produce a new word or phrase, using all the original letters exactly once; e.g., orchestra = carthorse, A decimal point = I'm a dot in place, Tom Marvolo Riddle = I am Lord Voldemort. Someone who...
in an appendix to his Description of Helioscopes,
where he wrote that he had found "a true mathematical and mechanical form of all manner of Arches for Building." He did not publish the solution of this anagram in his lifetime, but in 1705 his executor provided it as Ut pendet continuum flexile, sic stabit contiguum rigidum inversum, meaning "As hangs a flexible cable so, inverted, stand the touching pieces of an arch."
In 1691 Gottfried Leibniz
Gottfried Leibniz
Gottfried Wilhelm Leibniz was a German philosopher and mathematician. He wrote in different languages, primarily in Latin , French and German ....
, Christiaan Huygens, and Johann Bernoulli
Johann Bernoulli
Johann Bernoulli was a Swiss mathematician and was one of the many prominent mathematicians in the Bernoulli family...
derived the equation
Equation
An equation is a mathematical statement that asserts the equality of two expressions. In modern notation, this is written by placing the expressions on either side of an equals sign , for examplex + 3 = 5\,asserts that x+3 is equal to 5...
in response to a challenge by Jakob Bernoulli. David Gregory wrote a treatise on the catenary in 1697.
Euler proved in 1744 that the catenary is the curve which, when rotated about the x-axis, gives the surface of minimum surface area
Surface area
Surface area is the measure of how much exposed area a solid object has, expressed in square units. Mathematical description of the surface area is considerably more involved than the definition of arc length of a curve. For polyhedra the surface area is the sum of the areas of its faces...
(the catenoid
Catenoid
A catenoid is a three-dimensional surface made by rotating a catenary curve about its directrix. Not counting the plane, it is the first minimal surface to be discovered. It was found and proved to be minimal by Leonhard Euler in 1744. Early work on the subject was published also by Jean Baptiste...
) for the given bounding circles. Nicolas Fuss
Nicolas Fuss
Nicolas Fuss , also known as Nikolai Fuss, was a Swiss mathematician.Fuss was born in Basel, Switzerland. He moved to Saint Petersburg to serve as a mathematical assistant to Leonhard Euler from 1773–1783, and remained there until his death...
gave equations describing the equilibrium of a chain under any force in 1796.
The inverted catenary arch
Kiln
A kiln is a thermally insulated chamber, or oven, in which a controlled temperature regime is produced. Uses include the hardening, burning or drying of materials...
s. In this construction technique, the shape of a hanging chain of the desired dimensions is transferred to a form which is then used as a guide for the placement of bricks or other building material.
The Gateway Arch
Gateway Arch
The Gateway Arch, or Gateway to the West, is an arch that is the centerpiece of the Jefferson National Expansion Memorial in St. Louis, Missouri. It was built as a monument to the westward expansion of the United States...
in St. Louis, Missouri
St. Louis, Missouri
St. Louis is an independent city on the eastern border of Missouri, United States. With a population of 319,294, it was the 58th-largest U.S. city at the 2010 U.S. Census. The Greater St...
, United States
United States
The United States of America is a federal constitutional republic comprising fifty states and a federal district...
is sometimes said to be an (inverted) catenary, but this is incorrect. It is close to a more general curve called a flattened catenary, with equation y=Acosh(Bx). (A catenary would have AB=1.) While a catenary is the ideal shape for a freestanding arch of constant thickness, the Gateway Arch is narrower near the top. According to the U.S. National Historic Landmark
National Historic Landmark
A National Historic Landmark is a building, site, structure, object, or district, that is officially recognized by the United States government for its historical significance...
nomination for the arch, it is a "weighted catenary" instead. Its shape corresponds to the shape that a weighted chain, having lighter links in the middle, would form.
Catenary bridges
Simple suspension bridge
A simple suspension bridge is an early type of bridge that is supported entirely from anchors at either end, and has no towers or piers. However, it may have saddles...
or "catenary bridge," where the roadway follows the cable.
Stressed ribbon bridge
A stressed ribbon bridge is a tension structure . The suspension cables are embedded in the deck which follows a catenary arc between supports. Unlike the simple span the ribbon is stressed in compression, which adds to the stiffness of the structure...
is a more sophisticated structure with the same catenary shape.
However in a suspension bridge
Suspension bridge
A suspension bridge is a type of bridge in which the deck is hung below suspension cables on vertical suspenders. Outside Tibet and Bhutan, where the first examples of this type of bridge were built in the 15th century, this type of bridge dates from the early 19th century...
with a suspended roadway, the chains or cables support the weight of the bridge, and so do not hang freely. In most cases the roadway is flat, so when the weight of the cable is negligible compared with the weight being supported, the force exerted is uniform with respect to horizontal distance, and the result is a parabola, as discussed below (although the term "catenary" is often still used, in an informal sense). If the cable is heavy then the resulting curve is between a catenary and a parabola.
Anchoring of marine objects
The catenary form given by gravity is taken advantage of in its presence in heavy anchor rodes. An anchor rode (or anchor line) usually consists of chain and/or cable. Anchor rodes are used by ships, oilrigs, docks, floating wind turbineFloating wind turbine
A floating wind turbine is an offshore wind turbine mounted on a floating structure that allows the turbine to generate electricity in water depths where bottom-mounted towers are not feasible...
s, and other marine assets which must be anchored to the seabed.
When the rode is slack, the catenary curve presents a lower angle of pull on the anchor
Anchor
An anchor is a device, normally made of metal, that is used to connect a vessel to the bed of a body of water to prevent the vessel from drifting due to wind or current. The word derives from Latin ancora, which itself comes from the Greek ἄγκυρα .Anchors can either be temporary or permanent...
or mooring device than would be the case if it was nearly straight. This assists the performance of the anchor and raises the level of force it will resist before dragging. To maintain the catenary shape in the presence of wind, a heavy chain is needed, so that only larger ships in deeper water can rely on this effect – smaller boats must rely on the performance of the anchor itself.
Equation
The equation of a catenary in Cartesian coordinates has the form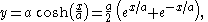where cosh is the hyperbolic cosine function
Hyperbolic function
In mathematics, hyperbolic functions are analogs of the ordinary trigonometric, or circular, functions. The basic hyperbolic functions are the hyperbolic sine "sinh" , and the hyperbolic cosine "cosh" , from which are derived the hyperbolic tangent "tanh" and so on.Just as the points form a...
.
The Whewell equation
Whewell equation
The Whewell equation of a plane curve is an equation that relates the tangential angle with arclength , where the tangential angle is angle between the tangent to the curve and the x-axis and the arc length is the distance along the curve from a fixed point...
for the catenary is
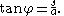
Differentiating gives
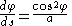
and eliminating
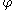gives the Cesàro equationCesàro equation
In geometry, the Cesàro equation of a plane curve is an equation relating curvature to arc length . It may also be given as an equation relating the radius of curvature to arc length. Two congruent curves will have the same Cesàro equation...
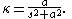
The radius of curvature
Osculating circle
In differential geometry of curves, the osculating circle of a sufficiently smooth plane curve at a given point p on the curve has been traditionally defined as the circle passing through p and a pair of additional points on the curve infinitesimally close to p...
is then
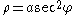
which is the length of the line normal to the curve between it and the x-axis.
Other properties
All catenary curves are similarSimilarity (geometry)
Two geometrical objects are called similar if they both have the same shape. More precisely, either one is congruent to the result of a uniform scaling of the other...
to each other. Changing the parameter a is equivalent to a uniform scaling of the curve.
A parabola rolled along a straight line traces out a catenary (see roulette
Roulette (curve)
In the differential geometry of curves, a roulette is a kind of curve, generalizing cycloids, epicycloids, hypocycloids, trochoids, and involutes....
) with its focus
Focus (geometry)
In geometry, the foci are a pair of special points with reference to which any of a variety of curves is constructed. For example, foci can be used in defining conic sections, the four types of which are the circle, ellipse, parabola, and hyperbola...
.
Square wheel
Square wheel
A square wheel is a wheel that, instead of being circular, has the shape of a square. While literal square wheels exist, a more common use is as a metaphor meaning stereotypically bad or naïve engineering ....
s can roll perfectly smoothly if the road has evenly spaced bumps in the shape of a series of inverted catenary curves. The wheels can be any regular polygon except a triangle, but the catenary must have parameters corresponding to the shape and dimensions of the wheels.
A charge
Electric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
in a uniform electric field
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
moves along a catenary (which tends to a parabola
Parabola
In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
if the charge velocity is much less than the speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
c).
The surface of revolution
Surface of revolution
A surface of revolution is a surface in Euclidean space created by rotating a curve around a straight line in its plane ....
with fixed radii at either end that has minimum surface area is a catenary revolved about the x-axis.
Over any horizontal interval, the ratio of the area under the caternary to its length equals a, independent of the interval selected. The catenary is the only plane curve other than a horizontal line with this property. Also, the geometric centroid of the area under a stretch of catenary is the midpoint of the perpendicular segment connecting the centroid of the curve itself and the x-axis.
Model of chains and arches
The chain (or cord, cable, rope, string, etc.) is idealized by assuming that it is so thin that it can be regarded as a curveCurve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
and that it is so flexible any force exerted by the chain itself is parallel to the chain. The analysis of the curve for an optimal arch is similar except that the forces of tension become forces of compression and everything is inverted.
An underlying principle is that the chain may be considered a rigid body once it has attained equilibrium. Equations which define the shape of the curve and the tension of the chain at each point may be derived by a careful inspection of the various forces acting on a segment using the fact that these forces must be in balance if the chain is in static equilibrium.
Let the path followed by the chain is given parametrically by
r = (x, y) = (x(s), y(s)) where s represents arc length
Arc length
Determining the length of an irregular arc segment is also called rectification of a curve. Historically, many methods were used for specific curves...
and r is the position vector. This is the natural parameterization and has the property that
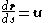
where u is a unit tangent vector.
A differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
for the curve may be derived as follows. Let c be the lowest point on the chain, called the vertex of the catenary,
and measure the parameter s from c. Assume r is to the right of c since the other case is implied by symmetry. The forces acting on section of the chain from c to r are the tension of the chain at c, the tension of the chain at r and the weight of the chain. The tension at c is tangent to the curve at c and is therefore horizontal, and it pulls the section to the left so it may be written (−T0, 0) where T0 is the magnitude of the force. The tension at r is parallel to the curve at r and pulls the section to the right, so it may be written Tu=(Tcos φ, Tsin φ), where T is the magnitude of the force and φ is the is the angle between the curve at r and the x-axis (see tangential angle
Tangential angle
In geometry, the tangential angle of a curve in the Cartesian plane, at a specific point, is the angle between the tangent line to the curve at the given point and the x-axis. In geometry, the tangential angle of a curve in the Cartesian plane, at a specific point, is the angle between the tangent...
). Finally, weight of the chain is represented by (0, −λgs) where λ is the mass per unit length and g is the acceleration of gravity.
The chain is in equilibrium so the sum of three forces is 0, therefore
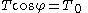
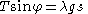
and dividing these
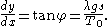
It is convenient to write
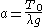
which is the length of chain whose weight is equal in magnitude to the tension at c. Then
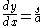
is an equation defining the curve.
It is immediate that the horizontal component of the tension, Tcos φ = λga is constant and the vertical component of the tension, Tsin φ = λgs is proportional to the length of chain between the r and the vertex.
Derivation of equations for the curve
The differential equation given above can be solved to produce equations for the curve.From
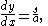
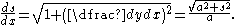
Then
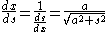
and
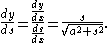
The second of these equations can be integrated to give
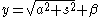
and by shifting the position of the x-axis, β can be taken to be 0. Then
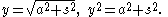
The x-axis thus chosen is called the directrix of the catenary.
It follows that the magnitude of the tension at a point T = λgy which is proportional to the distance between the point and the directrix.
The integral of expression for dx/ds can be found using standard techniques giving
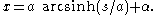
and, again, by shifting the position of the y-axis, α can be taken to be 0. Then
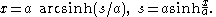
The y-axis thus chosen passes though the vertex and is called the axis of the catenary.
These results can be used to eliminate s giving
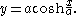
Alternative derivation
The differential equation can be solved using a different approach.From
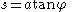
it follows
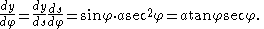
Integrating,
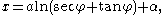
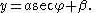
As before, the x and y-axes can be shifted so α and β can be taken to be 0. Then
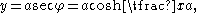
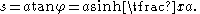
Determining parameters
The equation of a catenary suspended at given points A and A′ and with given length l can be determined as follows:Relabel if necessary so that A is to the left of A′ and let h and k be the vertical and horizontal distances from A to A′. Translate the axes so that the origin is at the vertex of the catenary so the equation of the curve is
and let the coordinates of A and A′ be (b, c) and (b′, c′) respectively. The curve passes through these points, so
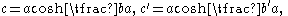
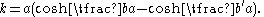
The lengths of the curve from the vertex to A and from the vertex to A′ are
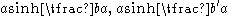
respectively, so the length from A to A′ is
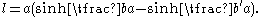
Then
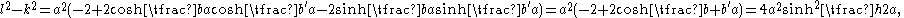
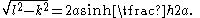
This is a transcendental equation in a and must be solved numerically. However, it can be shown with the methods of calculus that there is at most one solution with a>0 and so there is at most one position of equilibrium. Furthermore, a solution exists only when
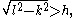
in other words l is greater than the distance from A to A′. That is, a solution exists only when the length of the chain is longer than the distance between the two points.
Nonuniform chains
If the density of the chain is variable then the analysis above can be adapted to produce equations for the curve given the density, or given the curve to find the density.Let w denote the weight per unit length of the chain, then the weight of the chain has magnitude
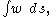
where the limits of integration are c and r. Balancing forces as before produces
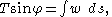
Differentiation gives
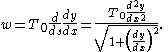
In terms of φ and the radius of curvature ρ this becomes
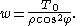
Suspension bridge curve
Suspension bridge
A suspension bridge is a type of bridge in which the deck is hung below suspension cables on vertical suspenders. Outside Tibet and Bhutan, where the first examples of this type of bridge were built in the 15th century, this type of bridge dates from the early 19th century...
with a horizontal roadway. If the weight of the roadway per unit length is w and the weight of the cable and the wire supporting the bridge is negligible in comparison, then the weight on the cable from c to r is wx where x is the horizontal distance between c to r. Proceeding a before gives the differential equation
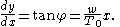
This is solved by simple integration to get
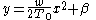
and so the cable follows a parabola. If weight of the cable and supporting wires are not negligible then the analysis is more difficult.
Catenary of equal strength
In a catenary of equal strength, cable is strengthened according to the magnitude of the tension at each point, so its resistance to breaking is constant along its length. Assuming that the strength of the cable is proportional to its density per unit length, the weight, w, per unit length of the chain can be written T/c, where c is constant, and the analysis for nonuniform chains can be applied.In this case the equations for tension are
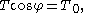
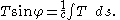
Combining gives
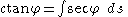
and by differentiation
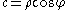
where ρ is the radius of curvature.
The solution to this is
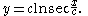
In this case, the curve has vertical asymptotes and this limits the span to πc. Other relations are
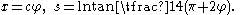
The curve was studied 1826 by Davies Gilbert
Davies Gilbert
Davies Gilbert FRS was a British engineer, author, and politician. He was elected to the Royal Society on 17 November 1791 and served as President of the Royal Society from 1827 to 1830....
and, apparently independently, by Gaspard-Gustave Coriolis
Gaspard-Gustave Coriolis
Gaspard-Gustave de Coriolis or Gustave Coriolis was a French mathematician, mechanical engineer and scientist. He is best known for his work on the supplementary forces that are detected in a rotating frame of reference. See the Coriolis Effect...
in 1836.
Elastic catenary
In an elasticElasticity (physics)
In physics, elasticity is the physical property of a material that returns to its original shape after the stress that made it deform or distort is removed. The relative amount of deformation is called the strain....
catenary, the chain is replaced by a spring which can stretch in response to tension. The spring is assumed to stretch in accordance with Hooke's Law
Hooke's law
In mechanics, and physics, Hooke's law of elasticity is an approximation that states that the extension of a spring is in direct proportion with the load applied to it. Many materials obey this law as long as the load does not exceed the material's elastic limit. Materials for which Hooke's law...
. Specifically, if p is the natural length of a section of spring, then the length of the spring with tension T applied has length
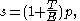
where E is a constant. In the catenary the value of T is variable, but ratio remains valid at a local level, so
The curve followed by an elastic spring can now be derived following a similar method as for the inelastic spring.
The equations for tension of the spring are
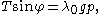
from which
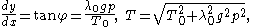
where p is the natural length of the segment from c to r and λ0 is the mass per unit length of the spring with no tension and g is the acceleration of gravity. Write
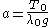
so
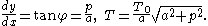
Parametric equations for the curve are now given by
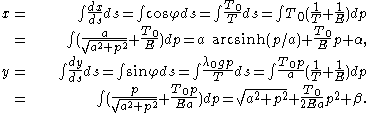
Again, the x and y-axes can be shifted so α and β can be taken to be 0. So
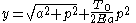
are parametric equations for the curve.
A chain under a general force
With no assumptions have been made regarding the force G acting on the chain, the following analysis can be made.First, let T=T(s) be the force of tension as a function of s. The chain is flexible so it can only exert a force parallel to itself. Since tension is defined as the force that the chain exerts on itself, T must be parallel to the chain. In other words,
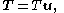
where T is the magnitude of T and u is the unit tangent vector.
Second, let G=G(s) be the external force per unit length acting on a small segment of a chain as a function of s. The forces acting on the segment of the chain between s and s+Δs are the force of tension T(s+Δs) at one end of the segment, the nearly opposite force −T(s) at the other end, and the external force acting on the segment which is
approximately GΔs. These forces must balance so
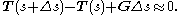
Divide by
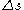and take the limit as 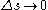to obtain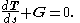These equations can be used as the starting point in the analysis of a flexible chain acting under any external force. In the case of the standard catenary, G = (0, −λg) where the chain has mass λ per unit length and g is the acceleration of gravity.
See also
- Overhead linesOverhead linesOverhead lines or overhead wires are used to transmit electrical energy to trams, trolleybuses or trains at a distance from the energy supply point...
- Roulette (curve)Roulette (curve)In the differential geometry of curves, a roulette is a kind of curve, generalizing cycloids, epicycloids, hypocycloids, trochoids, and involutes....
– an elliptic/hyperbolic catenary - TroposkeinTroposkeinIn physics and geometry, the troposkein is the curve an idealized rope assumes when anchored at its ends and spun around its long axis at a constant angular velocity. This shape is similar to the shape assumed by a skipping rope, and is independent of rotational speed in the absence of gravity,...
– the shape of a spun rope
External links
- Catenary at The Geometry CenterThe Geometry CenterThe Geometry Center was a mathematics research and education center at the University of Minnesota. It was established by the National Science Foundation in the late 1980s and closed in 1998. The focus of the Center's work was the use of computer graphics and visualization for research and...
- "Catenary of equal resistance" at Encyclopédie des Formes Mathématiques Remarquables
- "Catenary" at Visual Dictionary of Special Plane Curves
- Hanging With Galileo – mathematical derivation of formula for suspended and free-hanging chains; interactive graphical demo of parabolic versus hyperbolic suspensions.
- Catenary Demonstration Experiment – An easy way to demonstrate the Mathematical properties of a cosh using the hanging cable effect. Devised by Jonathan Lansey
- Catenary curve derived – The shape of a catenary is derived, plus examples of a chain hanging between 2 points of unequal height, including C program to calculate the curve.
- Cable Sag Error Calculator – Calculates the deviation from a straight line of a catenary curve and provides derivation of the calculator and references.
- Hexagonal Geodesic Domes – Catenary Domes, an article about creating catenary domes
- Dynamic as well as static cetenary curve equations derived – The equations governing the shape (static case) as well as dynamics (dynamic case) of a centenary is derived. Solution to the equations discussed.
- Ira Freeman "A General From of the Suspension Bridge Catenary" Bulletin of the AMS