Curve orientation
Encyclopedia
In mathematics
, a positively oriented curve is a planar simple closed curve (that is, a curve in the plane whose starting point is also the end point and which has no other self-intersections) such that when traveling on it one always has the curve interior to the left (and consequently, the curve exterior to the right). If in the above definition one interchanges left and right, one obtains a negatively oriented curve.
Crucial to this definition is the fact that every simple closed curve admits a well-defined interior; that follows from the Jordan curve theorem
.
All simple closed curves can be classified as negatively oriented (clockwise
), positively oriented (counterclockwise), or non-orientable
. The inner loop of a beltway road in the United States (or other countries where people drive on the right side of the road) would be an example of a negatively oriented (clockwise) curve. A circle
oriented counterclockwise is an example of a positively oriented curve. The same circle oriented clockwise would be a negatively oriented curve.
The concept of orientation of a curve is just a particular case of the notion of orientation
of a manifold
(that is, besides orientation of a curve one may also speak of orientation of a surface
, hypersurface
, etc.). Here, the interior and the exterior of a curve both inherit the usual orientation of the plane. The positive orientation on the curve is then the orientation it inherits as the boundary of its interior; the negative orientation is inherited from the exterior.
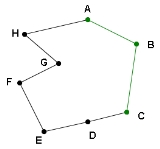
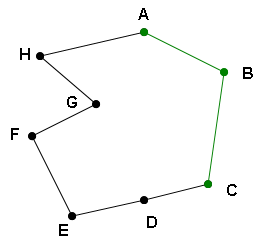 In two dimensions, given an ordered set of three or more connected vertices (points) (such as in connect-the-dots
In two dimensions, given an ordered set of three or more connected vertices (points) (such as in connect-the-dots
) which forms a simple polygon
, the orientation of the resulting polygon
is directly related to the sign of the angle at any vertex
of the convex hull
of the polygon, for example, of the angle ABC in the picture. In computations, the sign of the smaller angle formed by a pair of vectors is typically determined by the sign of the cross product of the vectors. The latter one may be calculated as the sign of the determinant
of their orientation matrix. In the particular case when the two vectors are defined by two line segment
s with common endpoint, such as the sides BA and BC of the angle ABC in our example, the orientation matrix may be defined as follows:
A formula for its determinant may be obtained, e.g., using the method of cofactor expansion: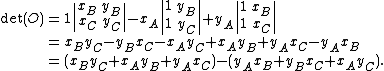
If the determinant is negative, then the polygon is oriented clockwise. If the determinant is positive, the polygon is oriented counterclockwise. The determinant is non-zero if points A, B, and C are non-collinear. In the above example, with points ordered A, B, C, etc., the determinant is negative, and therefore the polygon is clockwise.
One does not need to construct the convex hull of a polygon to find a suitable vertex. A common choice is the vertex of the polygon with the smallest X-coordinate. If there are several of them, the one with the smallest Y-coordinate is picked. It is guaranteed to be the vertex of the convex hull of the polygon. Alternatively, the vertex with the smallest Y-coordinate among the ones with the largest X-coordinates or the vertex with the smallest X-coordinate among the ones with the largest Y-coordinates (or any other of 8 "smallest, largest" X/Y combinations) will do as well.
If the orientation of a convex polygon
is sought, then, of course, any vertex may be picked.
For numerical reasons, the following equivalent formula for the determinant is commonly used:
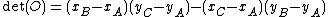
The latter formula has 4 multiplications less. What is more important in computer computations involved in most practical applications, such as computer graphics
of CAD, the absolute values of the multipliers are usually smaller (e.g., when A, B, C are within the same quadrant
), thus giving a smaller numerical error
or, in the extreme cases, avoiding the arithmetic overflow
.
When it is not known in advance that the sequence of points defines a simple polygon, the following things must be kept in mind.
For a self-intersecting polygon (complex polygon
) (or for any self-intersecting curve) there is no natural notion of the "interior", hence the orientation is not defined. At the same time, in geometry
and computer graphics
there are a number of concepts to replace the notion of the "interior" for closed non-simple curves; see, e.g., "flood fill
" and "winding number
".
In "mild" cases of self-intersection (degenerate polygons), when three consecutive points are allowed be on the same straight line and form a zero-degree angle, the concept of "interior" still makes sense, but an extra care must be taken in selection of the tested angle. In the given example, imagine point A to lie on segment BC. In this situation the angle ABC and its determinant will be 0, hence useless. A solution is to test consecutive corners along the polygon (BCD, DEF,...) until a non-sero determinant is found (unless all points lie on the same straight line). (Notice that the points C, D, E are on the same line and form a 180-degree angle with zero determinant.)
, convex
, or collinear (flat), we construct the matrix
If the determinant of this matrix is 0, then the sequence is collinear - neither concave nor convex. If the determinant has the same sign as that of the orientation matrix for the entire polygon, then the sequence is convex. If the signs differ, then the sequence is concave. In this example, the polygon is negatively oriented, but the determinant for the points F-G-H is positive, and so the sequence F-G-H is concave.
The following table illustrates rules for determining whether a sequence of points is convex, concave, or flat:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a positively oriented curve is a planar simple closed curve (that is, a curve in the plane whose starting point is also the end point and which has no other self-intersections) such that when traveling on it one always has the curve interior to the left (and consequently, the curve exterior to the right). If in the above definition one interchanges left and right, one obtains a negatively oriented curve.
Crucial to this definition is the fact that every simple closed curve admits a well-defined interior; that follows from the Jordan curve theorem
Jordan curve theorem
In topology, a Jordan curve is a non-self-intersecting continuous loop in the plane, and another name for a Jordan curve is a "simple closed curve"...
.
All simple closed curves can be classified as negatively oriented (clockwise
Clockwise
Circular motion can occur in two possible directions. A clockwise motion is one that proceeds in the same direction as a clock's hands: from the top to the right, then down and then to the left, and back to the top...
), positively oriented (counterclockwise), or non-orientable
Orientability
In mathematics, orientability is a property of surfaces in Euclidean space measuring whether or not it is possible to make a consistent choice of surface normal vector at every point. A choice of surface normal allows one to use the right-hand rule to define a "clockwise" direction of loops in the...
. The inner loop of a beltway road in the United States (or other countries where people drive on the right side of the road) would be an example of a negatively oriented (clockwise) curve. A circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
oriented counterclockwise is an example of a positively oriented curve. The same circle oriented clockwise would be a negatively oriented curve.
The concept of orientation of a curve is just a particular case of the notion of orientation
Orientation (mathematics)
In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...
of a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
(that is, besides orientation of a curve one may also speak of orientation of a surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
, hypersurface
Hypersurface
In geometry, a hypersurface is a generalization of the concept of hyperplane. Suppose an enveloping manifold M has n dimensions; then any submanifold of M of n − 1 dimensions is a hypersurface...
, etc.). Here, the interior and the exterior of a curve both inherit the usual orientation of the plane. The positive orientation on the curve is then the orientation it inherits as the boundary of its interior; the negative orientation is inherited from the exterior.
Orientation of a simple polygon

Connect the dots
Connect the dots, also known as dot to dot or join the dots is a form of puzzle containing a sequence of numbered dots. When a line is drawn connecting the dots the outline of an object is revealed. The puzzles often contain simple line art to enhance the image created or to assist in rendering a...
) which forms a simple polygon
Simple polygon
In geometry, a simple polygon is a closed polygonal chain of line segments in the plane which do not have points in common other than the common vertices of pairs of consecutive segments....
, the orientation of the resulting polygon
Polygon
In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
is directly related to the sign of the angle at any vertex
Vertex (geometry)
In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...
of the convex hull
Convex hull
In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
of the polygon, for example, of the angle ABC in the picture. In computations, the sign of the smaller angle formed by a pair of vectors is typically determined by the sign of the cross product of the vectors. The latter one may be calculated as the sign of the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of their orientation matrix. In the particular case when the two vectors are defined by two line segment
Line segment
In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...
s with common endpoint, such as the sides BA and BC of the angle ABC in our example, the orientation matrix may be defined as follows:

A formula for its determinant may be obtained, e.g., using the method of cofactor expansion:
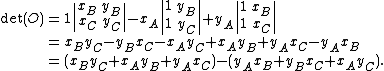
If the determinant is negative, then the polygon is oriented clockwise. If the determinant is positive, the polygon is oriented counterclockwise. The determinant is non-zero if points A, B, and C are non-collinear. In the above example, with points ordered A, B, C, etc., the determinant is negative, and therefore the polygon is clockwise.
Practical considerations
In practical applications, the following considerations are commonly taken into an account.One does not need to construct the convex hull of a polygon to find a suitable vertex. A common choice is the vertex of the polygon with the smallest X-coordinate. If there are several of them, the one with the smallest Y-coordinate is picked. It is guaranteed to be the vertex of the convex hull of the polygon. Alternatively, the vertex with the smallest Y-coordinate among the ones with the largest X-coordinates or the vertex with the smallest X-coordinate among the ones with the largest Y-coordinates (or any other of 8 "smallest, largest" X/Y combinations) will do as well.
If the orientation of a convex polygon
Convex polygon
In geometry, a polygon can be either convex or concave .- Convex polygons :A convex polygon is a simple polygon whose interior is a convex set...
is sought, then, of course, any vertex may be picked.
For numerical reasons, the following equivalent formula for the determinant is commonly used:
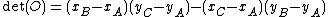
The latter formula has 4 multiplications less. What is more important in computer computations involved in most practical applications, such as computer graphics
Computer graphics
Computer graphics are graphics created using computers and, more generally, the representation and manipulation of image data by a computer with help from specialized software and hardware....
of CAD, the absolute values of the multipliers are usually smaller (e.g., when A, B, C are within the same quadrant
Quadrant
Quadrant may refer to:* A sector equal to one quarter of a circle, or half a semicircle, see Circular sector* The sectors of a two-dimensional cartesian coordinate system, see Cartesian coordinate system#Quadrants and octants...
), thus giving a smaller numerical error
Numerical error
In software engineering and mathematics, numerical error is the combined effect of two kinds of error in a calculation. The first is caused by the finite precision of computations involving floating-point or integer values...
or, in the extreme cases, avoiding the arithmetic overflow
Arithmetic overflow
The term arithmetic overflow or simply overflow has the following meanings.# In a computer, the condition that occurs when a calculation produces a result that is greater in magnitude than that which a given register or storage location can store or represent.# In a computer, the amount by which a...
.
When it is not known in advance that the sequence of points defines a simple polygon, the following things must be kept in mind.
For a self-intersecting polygon (complex polygon
Complex polygon
The term complex polygon can mean two different things:*In computer graphics, as a polygon which is neither convex nor concave.*In geometry, as a polygon in the unitary plane, which has two complex dimensions.-Computer graphics:...
) (or for any self-intersecting curve) there is no natural notion of the "interior", hence the orientation is not defined. At the same time, in geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
and computer graphics
Computer graphics
Computer graphics are graphics created using computers and, more generally, the representation and manipulation of image data by a computer with help from specialized software and hardware....
there are a number of concepts to replace the notion of the "interior" for closed non-simple curves; see, e.g., "flood fill
Flood fill
Flood fill, also called seed fill, is an algorithm that determines the area connected to a given node in a multi-dimensional array. It is used in the "bucket" fill tool of paint programs to determine which parts of a bitmap to fill with color, and in games such as Go and Minesweeper for determining...
" and "winding number
Winding number
In mathematics, the winding number of a closed curve in the plane around a given point is an integer representing the total number of times that curve travels counterclockwise around the point...
".
In "mild" cases of self-intersection (degenerate polygons), when three consecutive points are allowed be on the same straight line and form a zero-degree angle, the concept of "interior" still makes sense, but an extra care must be taken in selection of the tested angle. In the given example, imagine point A to lie on segment BC. In this situation the angle ABC and its determinant will be 0, hence useless. A solution is to test consecutive corners along the polygon (BCD, DEF,...) until a non-sero determinant is found (unless all points lie on the same straight line). (Notice that the points C, D, E are on the same line and form a 180-degree angle with zero determinant.)
Local concavity
Once the orientation of a polygon formed from an ordered set of vertices is known, the concavity of a local region of the polygon can be determined using a second orientation matrix. This matrix is composed of three consecutive vertices which are being examined for concavity. For example, in the polygon pictured above, if we wanted to know whether the sequence of points F-G-H is concaveConcave set
In mathematics, the notion of a "concave set" is not correct. A set that is not convex, is a non-convex set....
, convex
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
, or collinear (flat), we construct the matrix

If the determinant of this matrix is 0, then the sequence is collinear - neither concave nor convex. If the determinant has the same sign as that of the orientation matrix for the entire polygon, then the sequence is convex. If the signs differ, then the sequence is concave. In this example, the polygon is negatively oriented, but the determinant for the points F-G-H is positive, and so the sequence F-G-H is concave.
The following table illustrates rules for determining whether a sequence of points is convex, concave, or flat:
| Negatively oriented polygon (clockwise) | Positively oriented polygon (counterclockwise) | |
|---|---|---|
| determinant of orientation matrix for local points is negative | convex sequence of points | concave sequence of points |
| determinant of orientation matrix for local points is positive | concave sequence of points | convex sequence of points |
| determinant of orientation matrix for local points is 0 | collinear sequence of points | collinear sequence of points |
External links
- http://www.math.hmc.edu/faculty/gu/curves_and_surfaces/curves/_topology.html
- Curve orientation at MathWorldMathWorldMathWorld is an online mathematics reference work, created and largely written by Eric W. Weisstein. It is sponsored by and licensed to Wolfram Research, Inc. and was partially funded by the National Science Foundation's National Science Digital Library grant to the University of Illinois at...

