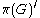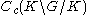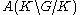Zonal spherical function
Encyclopedia
In mathematics
, a zonal spherical function or often just spherical function is a function on a locally compact group
G with compact subgroup K (often a maximal compact subgroup
) that arises as the matrix coefficient
of a K-invariant vector in an irreducible representation of G. The key examples are the matrix coefficients of the spherical principal series, the irreducible representations appearing in the decomposition of the unitary representation
of G on L2(G/K). In this case the commutant of G is generated by the algebra of biinvariant functions on G with respect to K acting by right convolution
. It is commutative if in addition G / K is a symmetric space
, for example when G is a connected semisimple Lie group with finite centre and K is a maximal compact subgroup. The matrix coefficients of the spherical principal series describe precisely the spectrum
of the corresponding
C* algebra generated by the biinvariant functions of compact support, often called a Hecke algebra. The spectrum of the commutative Banach *-algebra of biinvariant L1 functions is larger; when G is a semisimple Lie group with maximal compact subgroup K, additional characters come from matrix coefficients of the complementary series, obtained by analytic continuation of the spherical principal series.
Zonal spherical functions have been explicitly determined for real semisimple groups by Harish-Chandra
. For special linear group
s, they were independently discovered by Israel Gelfand
and Mark Naimark
. For complex groups, the theory simplifies significantly, because G is the complexification
of K, and the formulas are related to analytic continuations of the Weyl character formula
on K. The abstract functional analytic
theory of zonal spherical functions was first developed by Roger Godement
. Apart from their group theoretic interpretation, the zonal spherical functions for a semisimple Lie group G also provide a set of simultaneous eigenfunction
s for the natural action of the centre of the universal enveloping algebra
of G on L2(G/K), as differential operator
s on the symmetric space G/K. For semisimple p-adic Lie groups, the theory of zonal spherical functions and Hecke algebras was first developed by Satake and Ian G. Macdonald
. The analogues of the Plancherel theorem
and Fourier inversion formula in this setting generalise the eigenfunction expansions of Mehler, Weyl and Fock for singular ordinary differential equations
: they were obtained in full generality in the 1960s in terms of Harish-Chandra's c-function
.
The name "zonal spherical function" comes from the case when G is SO3(R)
acting on a 2-sphere and K is the subgroup fixing a point: in this case the zonal spherical functions can be regarded as certain functions on the sphere invariant under rotation about a fixed axis.
topological group
and K a compact
subgroup
and let H1 = L2(G/K). Thus H1 admits a unitary representation
π of G by left translation. This is a subrepresentation of the regular representation, since if H= L2(G) with left and right regular representation
s λ and ρ of G and P is the orthogonal projection
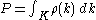
from H to H1 then H1 can naturally be identified with PH with the action of G given by the restriction of λ.
On the other hand by von Neumann's commutation theorem
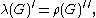
where S denotes the commutant of a set of operators S, so that
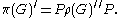
Thus the commutant of π is generated as a von Neumann algebra
by operators
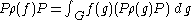
where f is a continuous function of compact support on G.
However Pρ(f) P is just the restriction of ρ(F) to H1, where
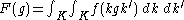
is the K-biinvariant continuous function of compact support obtained by averaging f by K on both sides.
Thus the commutant of π is generated by the restriction of the operators ρ(F) with F in
Cc(K\G/K), the K-biinvariant continuous functions of compact support on G.
These functions form a * algebra under convolution
with involution
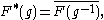
often called the Hecke algebra for the pair (G, K).
Let A(K\G/K) denote the C* algebra generated by the operators ρ(F) on H1.
The pair (G, K)
is said to be a Gelfand pair
if one, and hence all, of the following algebras are commutative:
Since A(K\G/K) is a commutative C* algebra, by the Gelfand–Naimark theorem
it has the form C0(X),
where X is the locally compact space of norm continuous * homomorphism
s of A(K\G/K) into C.
A concrete realization of the * homomorphisms in X as K-biinvariant uniformly bounded functions on G is obtained as follows.
Because of the estimate
the representation π of Cc(K\G/K) in A(K\G/K) extends by continuity
to L1(K\G/K), the * algebra of K-biinvariant integrable functions. The image forms
a dense * subalgebra of A(K\G/K). The restriction of a * homomorphism χ continuous for the operator norm is
also continuous for the norm ||·||1. Since the Banach space dual
of L1 is L∞,
it follows that
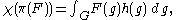
for some unique uniformly bounded K-biinvariant function h on G. These functions h are exactly the zonal spherical functions for the pair (G, K).
These are easy consequences of the fact that the bounded linear functional χ defined by h is a homomorphism. Properties 2, 3 and 4 or properties 3, 4 and 5 characterize zonal spherical functions. A more general class of zonal spherical functions can be obtained by dropping positive definiteness from the conditions, but for these functions there is no longer any connection
with unitary representation
s. For semisimple Lie groups, there is a further characterization as eigenfunctions of
invariant differential operators on G/K (see below).
In fact, as a special case of the Gelfand–Naimark–Segal construction, there is one-one correspondence between
irreducible representations σ of G having a unit vector v fixed by K and zonal spherical functions
h given by
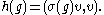
Such irreducible representations are often described as having class one. They are precisely the irreducible representations required to decompose the induced representation
π on H1. Each representation σ extends uniquely by continuity
to A(K\G/K), so that each zonal spherical function satisfies
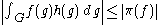
for f in A(K\G/K). Moreover, since the commutant π(G)' is commutative,
there is a unique probability measure μ on the space of * homomorphisms X such that
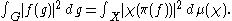
μ is called the Plancherel measure
. Since π(G)' is the centre
of the von Neumann algebra generated by G, it also gives the measure associated with the direct integral
decomposition of H1 in terms of the irreducible representations σχ.
Lie group
, then, thanks to the work of Cartan
, Malcev
, Iwasawa
and Chevalley
, G has a maximal compact subgroup
, unique up to conjugation. In this case K is connected and the quotient G/K is diffeomorphic to a Euclidean space. When G is in addition semisimple, this can be seen directly using the Cartan decomposition
associated to the symmetric space
G/K, a generalisation of the polar decomposition of invertible matrices. Indeed if τ is the associated period two automorphism of G with fixed point subgroup K, then
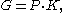
where
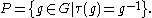
Under the exponential map
, P is diffeomorphic to the -1 eigenspace of τ in the Lie algebra
of G.
Since τ preserves K, it induces an automorphism of the Hecke algebra Cc(K\G/K). On the
other hand, if F lies in Cc(K\G/K), then
so that τ induces an anti-automorphism, because inversion does. Hence, when G is semisimple,
More generally the same argument gives the following criterion of Gelfand for (G,K) to be a Gelfand pair:
The two most important examples covered by this are when:
The three cases cover the three types of symmetric space
s G/K:
of G invariant under τ, such that T
P is a maximal torus in P, and set
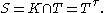
S is the direct product of a torus and an elementary abelian 2-group
.
In 1929 Élie Cartan
found a rule to determine the decomposition of L2(G/K) into the direct sum of finite-dimensional irreducible representations of G, which was proved rigorously only in 1970 by Sigurdur Helgason
. Because the commutant of G on L2(G/K) is commutative, each irreducible representation appears with multiplicity one. By Frobenius reciprocity for compact groups, the irreducible representations V that occur are precisely those admitting a non-zero vector fixed by K.
From the representation theory of compact semisimple groups
, irreducible representations of G are classified by their highest weight
. This is specified by a homomorphism of the maximal torus T into T.
The Cartan–Helgason theorem states that
The corresponding irreducible representations are called spherical representations.
The theorem can be proved using the Iwasawa decomposition
:
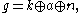
where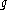
, 
, 
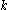are the complexifications of the Lie algebra
s of G, K, A = T
P and
summed over all eigenspaces for T in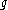
corresponding to positive roots
α not fixed by τ.
Let V be a spherical representation with highest weight vector v0 and K-fixed vector vK. Since v0 is an eigenvector of the solvable Lie algebra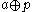
, the Poincaré–Birkhoff–Witt theorem
implies that the K-module generated by v0 is the whole of V. If Q is the orthogonal projection onto the fixed points of K in V obtained by averaging over G with respect to Haar measure
, it follows that
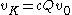
for some non-zero constant c. Because vK is fixed by S and v0 is an eigenvector for S, the subgroup S must actually fix v0, an equivalent form of the triviality condition on S.
Conversely if v0 is fixed by S, then it can be shown that the matrix coefficient
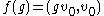
is non-negative on K. Since f(1) > 0, it follows that (Qv0, v0) > 0 and hence that Qv0 is a non-zero vector fixed by K.
. If A is a maximal Abelian subgroup of G contained in P, then A is isomorphic to its Lie algebra under the exponential map and, as a further generalisation
of the polar decomposition of matrices, every element of P is conjugate under K to an element of A, so that
There is also an associated Iwasawa decomposition
where N is a closed nilpotent subgroup, diffeomorphic to its Lie algebra under the exponential map and normalised by A. Thus
S=AN is a closed solvable subgroup
of G, the semidirect product
of N by A, and G = KS.
If α in Hom(A,T) is a character
of A, then α extends to a character of S, by defining it to be trivial on N. There is a corresponding unitary
induced representation
σ of G on L2(G/S) = L2(K), a so-called (spherical) principal series representation
.
This representation can be described explicitly as follows. Unlike G and K, the solvable Lie group S is not unimodular. Let dx denote left invariant Haar measure on S and ΔS the modular function of S. Then
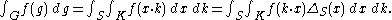
The principal series representation σ is realised on L2(K) as
where
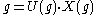
is the Iwasawa decomposition of g with U(g) in K and X(g) in S and
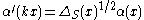
for k in K and x in S.
The representation σ is irreducible, so that if v denotes the constant function 1 on K, fixed by K,
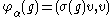
defines a zonal spherical function of G.
Computing the inner product above leads to Harish-Chandra's formula for the zonal spherical function
as an integral over K.
Harish-Chandra proved that these zonal spherical functions exhaust the characters of the C* algebra generated by the Cc(K \ G / K) acting by right convolution on L2(G / K). He also showed that two different characters α and β give the same zonal spherical function if and only if α = β·s, where s is in the Weyl group
of A
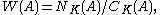
the quotient of the normaliser of A in K by its centraliser, a finite reflection group.
It can also be verified directly that this formula defines a zonal spherical function, without using representation theory. The proof for general semisimple Lie groups that every zonal spherical formula arises in this way requires the detailed study of G-invariant differential operators on G/K and their simultaneous eigenfunctions (see below). In the case of complex semisimple groups, Harish-Chandra and Felix Berezin
realised independently that the formula simplified considerably and could be proved more directly.
The remaining positive-definite zonal spherical functions are given
by Harish-Chandra's formula with α in Hom(A,C*) instead of Hom(A,T). Only certain α are permitted and the corresponding irreducible
representations arise as analytic continuations of the spherical principal series. This so-called "complementary series" was first studied by for G = SL(2,R) and by and for G = SL(2,C).
Subsequently in the 1960s, the construction of a complementary series by analytic continuation of the spherical principal series was systematically developed for general semisimple Lie groups by Ray Kunze, Elias Stein and Bertram Kostant
. Since these irreducible representations are not tempered
, they are not usually required for harmonic analysis on G (or G / K).
of G fixed under the adjoint action of K. As for the commutant of G on L2(G/K) and the corresponding Hecke algebra, this algebra of operators is commutative; indeed it is a subalgebra of the algebra of mesurable operators
affiliated with the commutant π(G)', an Abelian von Neumann algebra. As Harish-Chandra proved, it is isomorphic to the algebra of W(A)-invariant polynomials on the Lie algebra of A, which itself is a polynomial ring
by the Chevalley–Shephard–Todd theorem
on polynomial invariants of finite reflection groups. The simplest invariant differential operator on G/K is the Laplacian operator; up to a sign this operator is just the image under π of the Casimir operator in the centre of the universal enveloping algebra of G.
Thus a normalised positive definite K-biinvariant function f on G is a zonal spherical function if and only if for each D in D(G/K) there is a constant λD such that
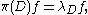
i.e. f is a simultaneous eigenfunction
of the operators π(D).
If ψ is a zonal spherical function, then, regarded as a function on G/K, it is an eigenfunction of the Laplacian
there, an elliptic differential operator with real analytic coefficients. By analytic elliptic regularity,
ψ is a real analytic function on G/K, and hence G.
Harish-Chandra used these facts about the structure of the invariant operators to prove that his formula gave all zonal spherical functions for real semisimple Lie groups. Indeed the commutativity of the commutant implies that the simultaneous eigenspaces of the algebra of invariant differential operators all have dimension one; and the polynomial structure of this algebra forces the simultaneous eigenvalues to be precisely those already associated with Harish-Chandra's formula.
of the compact Lie group K = SU(2) and the double cover of the Lorentz group
. The infinite-dimensional representations of the Lorentz group were first studied by Dirac
in 1945, who considered the discrete series representations, which he termed expansors. A systematic study was taken up shortly afterwards by Harish-Chandra, Gelfand–Naimark and
Bargmann. The irreducible representations of class one, corresponding to the zonal spherical functions, can be determined easily using the radial
component of the Laplacian operator.
Indeed any unimodular complex 2×2 matrix g admits a unique polar decomposition g = pv with v unitary and p positive. In turn
p = uau*, with u unitary and a a diagonal matrix with positive entries. Thus g = uaw with w = u* v, so that any K-biinvariant function on G corresponds to a function of the diagonal matrix
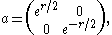
invariant under the Weyl group. Identifying G/K with hyperbolic 3-space, the zonal hyperbolic functions ψ correspond to radial functions that are eigenfunctions of the Laplacian. But in terms of the radial coordinate r, the Laplacian is given by
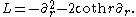
Setting f(r) = sinh (r)·ψ(r), it follows that f is an odd function of r and an eigenfunction of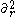
.
Hence
where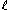
is real.
There is a similar elementary treatment for the generalized Lorentz groups SO(N,1) in and (recall that SO0(3,1) = SL(2,C) / ±I).
of its maximal compact subgroup K. If
and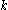 
are their Lie algebras, then
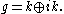
Let T be a maximal torus
in K with Lie algebra
. Then
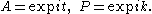
Let
be the Weyl group
of T in K. Recall characters
in Hom(T,T) are called weights
and
can be identified with elements of the weight lattice Λ in
Hom(
, R) =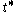 
.
There is a natural ordering on weights and very finite-dimensional
irreducible representation (π, V) of K has a unique highest weight
λ. The weights of the adjoint representation
of K
on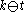
are called roots
and ρ is used to denote half the sum of the positive roots α,
Weyl's character formula asserts that for z = exp X in T
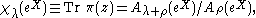
where, for μ in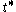
, Aμ denotes the antisymmetrisation
and ε denotes the sign character of the finite reflection group W.
Weyl's denominator formula expresses the denominator Aρ as a product:
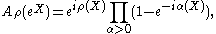
where the product is over the positive roots.
Weyl's dimension formula asserts that
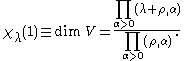
where the inner product on
is that associated with the Killing form
on
.
Now
The Berezin–Harish–Chandra formula asserts that for X in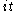
In other words:
One of the simplest proofs of this formula involves the radial component on A of the Laplacian on G, a proof formally parallel to Helgason's reworking of Freudenthal
's classical proof of the Weyl character formula
, using the radial component on T of the Laplacian on K.
In the latter case the class function
s on K can be identified with W-invariant functions on T. The
radial component of ΔK on T is just the expression for the restriction of ΔK to W-invariant functions on T, where
it is given by the formula
where
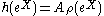
for X in
. If χ is a character with highest weight λ, it follows that φ = h·χ satisfies
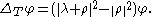
Thus for every weight μ with non-zero Fourier coefficient in φ,
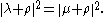
The classical argument of Freudenthal shows that μ + ρ must have the form s(λ + ρ) for some s in W, so the character formula
follows from the antisymmetry of φ.
Similarly K-biinvariant functions on G can be identified with W(A)-invariant functions on A. The
radial component of ΔG on A is just the expression for the restriction of ΔG to W(A)-invariant functions on A.
It is given by the formula
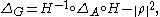
where
for X in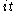
.
The Berezin–Harish–Chandra formula for a zonal spherical function φ can be established by introducing the antisymmetric function
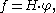
which is an eigenfunction of the Laplacian ΔA. Since K is generated by copies of subgroups that are homomorphic images of SU(2) corresponding to simple root
s, its complexification G is generated by the corresponding homomorphic images of SL(2,C). The formula for zonal spherical functions of SL(2,C) implies that f is a periodic function
on
with respect to some sublattice
. Antisymmetry under the Weyl group and the argument of Freudenthal again imply that ψ must have the stated form up to a multiplicative constant, which can be determined using the Weyl dimension formula.
's important work on the spectral theory of ordinary differential equations
. The radial part of the Laplacian in this case leads to a hypergeometric differential equation
, the theory of which was treated in detail by Weyl. Weyl's approach was subsequently generalised by Harish-Chandra to study zonal spherical functions and the corresponding Plancherel theorem for more general semimisimple Lie groups. Following the work of Dirac on the discrete series representations of SL(2,R), the general theory of unitary irreducible representations of SL(2,R) was developed independently by Bargmann, Harish-Chandra and Gelfand–Naimark. The irreducible representations of class one, or equivalently the theory of zonal spherical functions, form an important special case of this theory.
The group G = SL(2,R) is a double cover of the 3-dimensional Lorentz group
SO(2,1), the symmetry group
of the hyperbolic plane
with its Poincaré metric
. It acts by Moebius transformations. The upper half-plane can be identified with the unit disc by the Cayley transform
. Under this identification G becomes identified with the group SU(1,1), also acting by Moebius transformations. Because the action is
transitive, both spaces can be identified with G/K, where K = SO(2). The metric is invariant under G and the associated Laplacian is G-invariant, coinciding with the image of the Casimir operator. In the upper half-plane model the Laplacian is given by the formula
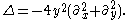
If s is a complex number and z = x + i y with y > 0, the function
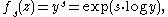
is an eigenfunction of Δ:
Since Δ commutes with G, any left translate of fs is also an eigenfunction with the same eigenvalue. In particular, averaging over K, the function
is a K-invariant eigenfunction of Δ on G/K. When
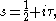
with τ real, these functions give all the zonal spherical functions on G. As with Harish-Chandra's more general formula for semisimple Lie groups, φs is a zonal spherical function because it is the matrix coefficient corresponding to a vector fixed by K in the principal series. Various arguments are available to prove that there are no others. One of the simplest classical Lie algebra
ic arguments is to note that, since Δ is an elliptic operator with analytic coefficients, by analytic elliptic regularity any eigenfunction is necessarily real analytic.
Hence, if the zonal spherical function corresponds is the matrix coefficient for a vector v and representation σ, the vector v is an analytic vector
for G and
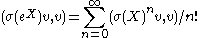
for X in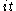
. The infinitesimal form of the irreducible unitary representations with a vector fixed by K were worked out classically by Bargmann. They correspond precisely to the principal series of SL(2,R). It follows that the zonal spherical function corresponds to a principal series representation.
Another classical argument proceeds by showing that on radial functions the Laplacian has the form
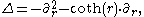
so that, as a function of r, the zonal spherical function φ(r) must satisfy the ordinary differential equation
for some constant α. The change of variables t = sinh r transforms this equation into the hypergeometric differential equation
. The general solution in terms of Legendre functions of complex index is given by
where α = ρ(ρ+1). Further restrictions on ρ are imposed by boundedness and positive-definiteness of the zonal spherical function on G.
There is yet another approach, due to Mogens Flensted-Jensen, which derives the properties of the zonal spherical functions on SL(2,R),
including the Plancherel formula, from the corresponding results for SL(2,C), which are simple consequences of the Plancherel formula and Fourier inversion formula for R. This "method of descent" works more generally, allowing results for a real semisimple Lie group to be derived by descent from the corresponding results for its complexification.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a zonal spherical function or often just spherical function is a function on a locally compact group
Locally compact group
In mathematics, a locally compact group is a topological group G which is locally compact as a topological space. Locally compact groups are important because they have a natural measure called the Haar measure. This allows one to define integrals of functions on G.Many of the results of finite...
G with compact subgroup K (often a maximal compact subgroup
Maximal compact subgroup
In mathematics, a maximal compact subgroup K of a topological group G is a subgroup K that is a compact space, in the subspace topology, and maximal amongst such subgroups....
) that arises as the matrix coefficient
Matrix coefficient
In mathematics, a matrix coefficient is a function on agroup of a special form, which depends on a linear representation of the group and additional data...
of a K-invariant vector in an irreducible representation of G. The key examples are the matrix coefficients of the spherical principal series, the irreducible representations appearing in the decomposition of the unitary representation
Unitary representation
In mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
of G on L2(G/K). In this case the commutant of G is generated by the algebra of biinvariant functions on G with respect to K acting by right convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
. It is commutative if in addition G / K is a symmetric space
Symmetric space
A symmetric space is, in differential geometry and representation theory, a smooth manifold whose group of symmetries contains an "inversion symmetry" about every point...
, for example when G is a connected semisimple Lie group with finite centre and K is a maximal compact subgroup. The matrix coefficients of the spherical principal series describe precisely the spectrum
Spectrum
A spectrum is a condition that is not limited to a specific set of values but can vary infinitely within a continuum. The word saw its first scientific use within the field of optics to describe the rainbow of colors in visible light when separated using a prism; it has since been applied by...
of the corresponding
C* algebra generated by the biinvariant functions of compact support, often called a Hecke algebra. The spectrum of the commutative Banach *-algebra of biinvariant L1 functions is larger; when G is a semisimple Lie group with maximal compact subgroup K, additional characters come from matrix coefficients of the complementary series, obtained by analytic continuation of the spherical principal series.
Zonal spherical functions have been explicitly determined for real semisimple groups by Harish-Chandra
Harish-Chandra
Harish-Chandra was an Indian mathematician, who did fundamental work in representation theory, especially Harmonic analysis on semisimple Lie groups. -Life:...
. For special linear group
Special linear group
In mathematics, the special linear group of degree n over a field F is the set of n×n matrices with determinant 1, with the group operations of ordinary matrix multiplication and matrix inversion....
s, they were independently discovered by Israel Gelfand
Israel Gelfand
Israel Moiseevich Gelfand, also written Israïl Moyseyovich Gel'fand, or Izrail M. Gelfand was a Soviet mathematician who made major contributions to many branches of mathematics, including group theory, representation theory and functional analysis...
and Mark Naimark
Mark Naimark
Mark Aronovich Naimark was a Soviet mathematician.He was born in Odessa, Russian Empire into a Jewish family and died in Moscow, USSR...
. For complex groups, the theory simplifies significantly, because G is the complexification
Complexification
In mathematics, the complexification of a real vector space V is a vector space VC over the complex number field obtained by formally extending scalar multiplication to include multiplication by complex numbers. Any basis for V over the real numbers serves as a basis for VC over the complex...
of K, and the formulas are related to analytic continuations of the Weyl character formula
Weyl character formula
In mathematics, the Weyl character formula in representation theory describes the characters of irreducible representations of compact Lie groups in terms of their highest weights. It was proved by ....
on K. The abstract functional analytic
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
theory of zonal spherical functions was first developed by Roger Godement
Roger Godement
Roger Godement is a French mathematician, known for his work in functional analysis, and also his expository books.He started as a student at the École normale supérieure in 1940, where he became a student of Henri Cartan...
. Apart from their group theoretic interpretation, the zonal spherical functions for a semisimple Lie group G also provide a set of simultaneous eigenfunction
Eigenfunction
In mathematics, an eigenfunction of a linear operator, A, defined on some function space is any non-zero function f in that space that returns from the operator exactly as is, except for a multiplicative scaling factor. More precisely, one has...
s for the natural action of the centre of the universal enveloping algebra
Universal enveloping algebra
In mathematics, for any Lie algebra L one can construct its universal enveloping algebra U. This construction passes from the non-associative structure L to a unital associative algebra which captures the important properties of L.Any associative algebra A over the field K becomes a Lie algebra...
of G on L2(G/K), as differential operator
Differential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
s on the symmetric space G/K. For semisimple p-adic Lie groups, the theory of zonal spherical functions and Hecke algebras was first developed by Satake and Ian G. Macdonald
Ian G. Macdonald
Ian Grant Macdonald is a British mathematician known for his contributions to symmetric functions, special functions, Lie algebra theory and other aspects of algebraic combinatorics ....
. The analogues of the Plancherel theorem
Plancherel theorem
In mathematics, the Plancherel theorem is a result in harmonic analysis, proved by Michel Plancherel in 1910. It states that the integral of a function's squared modulus is equal to the integral of the squared modulus of its frequency spectrum....
and Fourier inversion formula in this setting generalise the eigenfunction expansions of Mehler, Weyl and Fock for singular ordinary differential equations
Spectral theory of ordinary differential equations
In mathematics, the spectral theory of ordinary differential equations is the part of spectral theory concerned with the determination of the spectrum and eigenfunction expansion associated with a linear ordinary differential equation...
: they were obtained in full generality in the 1960s in terms of Harish-Chandra's c-function
Harish-Chandra's c-function
In mathematics, Harish-Chandra's c-function is a function related to the intertwining operator between two principal series representations, that appears in the Plancherel measure for semisimple Lie groups...
.
The name "zonal spherical function" comes from the case when G is SO3(R)
acting on a 2-sphere and K is the subgroup fixing a point: in this case the zonal spherical functions can be regarded as certain functions on the sphere invariant under rotation about a fixed axis.
Definitions
Let G be a locally compact unimodularUnimodular
In mathematics, unimodular may refer to any of the following:* unimodular lattice* unimodular matrix* unimodular polynomial matrix* unimodular form* unimodular group...
topological group
Topological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
and K a compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
and let H1 = L2(G/K). Thus H1 admits a unitary representation
Unitary representation
In mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
π of G by left translation. This is a subrepresentation of the regular representation, since if H= L2(G) with left and right regular representation
Regular representation
In mathematics, and in particular the theory of group representations, the regular representation of a group G is the linear representation afforded by the group action of G on itself by translation....
s λ and ρ of G and P is the orthogonal projection
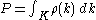
from H to H1 then H1 can naturally be identified with PH with the action of G given by the restriction of λ.
On the other hand by von Neumann's commutation theorem
Commutation theorem
In mathematics, a commutation theorem explicitly identifies the commutant of a specific von Neumann algebra acting on a Hilbert space in the presence of a trace. The first such result was proved by F.J...
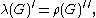
where S denotes the commutant of a set of operators S, so that
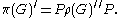
Thus the commutant of π is generated as a von Neumann algebra
Von Neumann algebra
In mathematics, a von Neumann algebra or W*-algebra is a *-algebra of bounded operators on a Hilbert space that is closed in the weak operator topology and contains the identity operator. They were originally introduced by John von Neumann, motivated by his study of single operators, group...
by operators
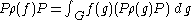
where f is a continuous function of compact support on G.
However Pρ(f) P is just the restriction of ρ(F) to H1, where
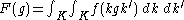
is the K-biinvariant continuous function of compact support obtained by averaging f by K on both sides.
Thus the commutant of π is generated by the restriction of the operators ρ(F) with F in
Cc(K\G/K), the K-biinvariant continuous functions of compact support on G.
These functions form a * algebra under convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
with involution
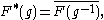
often called the Hecke algebra for the pair (G, K).
Let A(K\G/K) denote the C* algebra generated by the operators ρ(F) on H1.
The pair (G, K)
is said to be a Gelfand pair
Gelfand pair
In mathematics, the expression Gelfand pair is a pair consisting of a group G and a subgroup K that satisfies a certain property on restricted representations. The theory of Gelfand pairs is closely related to the topic of spherical functions in the classical theory of special functions, and to...
if one, and hence all, of the following algebras are commutative:
Since A(K\G/K) is a commutative C* algebra, by the Gelfand–Naimark theorem
Gelfand–Naimark theorem
In mathematics, the Gelfand–Naimark theorem states that an arbitrary C*-algebra A is isometrically *-isomorphic to a C*-algebra of bounded operators on a Hilbert space...
it has the form C0(X),
where X is the locally compact space of norm continuous * homomorphism
Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
s of A(K\G/K) into C.
A concrete realization of the * homomorphisms in X as K-biinvariant uniformly bounded functions on G is obtained as follows.
Because of the estimate
the representation π of Cc(K\G/K) in A(K\G/K) extends by continuity
to L1(K\G/K), the * algebra of K-biinvariant integrable functions. The image forms
a dense * subalgebra of A(K\G/K). The restriction of a * homomorphism χ continuous for the operator norm is
also continuous for the norm ||·||1. Since the Banach space dual
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
of L1 is L∞,
it follows that
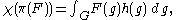
for some unique uniformly bounded K-biinvariant function h on G. These functions h are exactly the zonal spherical functions for the pair (G, K).
Properties
A zonal spherical function h has the following properties:- h is uniformly continuous on G
-
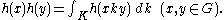
- h(1) =1 (normalisation)
- h is a positive definite functionPositive definite function on a groupIn operator theory, a positive-definite function on a group relates the notions of positivity, in the context of Hilbert spaces, and algebraic groups...
on G - f * h is proportional to h for all f in Cc(K\G/K).
These are easy consequences of the fact that the bounded linear functional χ defined by h is a homomorphism. Properties 2, 3 and 4 or properties 3, 4 and 5 characterize zonal spherical functions. A more general class of zonal spherical functions can be obtained by dropping positive definiteness from the conditions, but for these functions there is no longer any connection
with unitary representation
Unitary representation
In mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
s. For semisimple Lie groups, there is a further characterization as eigenfunctions of
invariant differential operators on G/K (see below).
In fact, as a special case of the Gelfand–Naimark–Segal construction, there is one-one correspondence between
irreducible representations σ of G having a unit vector v fixed by K and zonal spherical functions
h given by
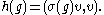
Such irreducible representations are often described as having class one. They are precisely the irreducible representations required to decompose the induced representation
Induced representation
In mathematics, and in particular group representation theory, the induced representation is one of the major general operations for passing from a representation of a subgroup H to a representation of the group G itself. It was initially defined as a construction by Frobenius, for linear...
π on H1. Each representation σ extends uniquely by continuity
to A(K\G/K), so that each zonal spherical function satisfies
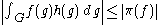
for f in A(K\G/K). Moreover, since the commutant π(G)' is commutative,
there is a unique probability measure μ on the space of * homomorphisms X such that
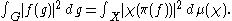
μ is called the Plancherel measure
Plancherel measure
In mathematics, Plancherel measure is a probability measure defined on the set of irreducible representations of a finite group G. In some cases the term Plancherel measure is applied specifically in the context of the group G being the finite symmetric group S_n – see below...
. Since π(G)' is the centre
Von Neumann algebra
In mathematics, a von Neumann algebra or W*-algebra is a *-algebra of bounded operators on a Hilbert space that is closed in the weak operator topology and contains the identity operator. They were originally introduced by John von Neumann, motivated by his study of single operators, group...
of the von Neumann algebra generated by G, it also gives the measure associated with the direct integral
Direct integral
In mathematics and functional analysis a direct integral is a generalization of the concept of direct sum. The theory is most developed for direct integrals of Hilbert spaces and direct integrals of von Neumann algebras. The concept was introduced in 1949 by John von Neumann in one of the papers...
decomposition of H1 in terms of the irreducible representations σχ.
Gelfand pairs
If G is a connectedConnectedness
In mathematics, connectedness is used to refer to various properties meaning, in some sense, "all one piece". When a mathematical object has such a property, we say it is connected; otherwise it is disconnected...
Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
, then, thanks to the work of Cartan
Élie Cartan
Élie Joseph Cartan was an influential French mathematician, who did fundamental work in the theory of Lie groups and their geometric applications...
, Malcev
Anatoly Maltsev
Anatoly Ivanovich Maltsev was born in Misheronsky, near Moscow, and died in Novosibirsk, USSR. He was a mathematician noted for his work on the decidability of various algebraic groups...
, Iwasawa
Kenkichi Iwasawa
Kenkichi Iwasawa was a Japanese mathematician who is known for his influence on algebraic number theory.Iwasawa was born in Shinshuku-mura, a town near Kiryū, in Gunma Prefecture...
and Chevalley
Claude Chevalley
Claude Chevalley was a French mathematician who made important contributions to number theory, algebraic geometry, class field theory, finite group theory, and the theory of algebraic groups...
, G has a maximal compact subgroup
Maximal compact subgroup
In mathematics, a maximal compact subgroup K of a topological group G is a subgroup K that is a compact space, in the subspace topology, and maximal amongst such subgroups....
, unique up to conjugation. In this case K is connected and the quotient G/K is diffeomorphic to a Euclidean space. When G is in addition semisimple, this can be seen directly using the Cartan decomposition
Cartan decomposition
The Cartan decomposition is a decomposition of a semisimple Lie group or Lie algebra, which plays an important role in their structure theory and representation theory. It generalizes the polar decomposition of matrices.- Cartan involutions on Lie algebras :...
associated to the symmetric space
Symmetric space
A symmetric space is, in differential geometry and representation theory, a smooth manifold whose group of symmetries contains an "inversion symmetry" about every point...
G/K, a generalisation of the polar decomposition of invertible matrices. Indeed if τ is the associated period two automorphism of G with fixed point subgroup K, then
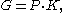
where
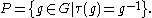
Under the exponential map
Exponential map
In differential geometry, the exponential map is a generalization of the ordinary exponential function of mathematical analysis to all differentiable manifolds with an affine connection....
, P is diffeomorphic to the -1 eigenspace of τ in the Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
of G.
Since τ preserves K, it induces an automorphism of the Hecke algebra Cc(K\G/K). On the
other hand, if F lies in Cc(K\G/K), then
- F(τg) = F(g−1),
so that τ induces an anti-automorphism, because inversion does. Hence, when G is semisimple,
- the Hecke algebra is commutative
- (G,K) is a Gelfand pair.
More generally the same argument gives the following criterion of Gelfand for (G,K) to be a Gelfand pair:
- G is a unimodular locally compact group;
- K is a compact subgroup arising as the fixed points of a period two automorphism τ of G;
- G =K·P (not necessarily a direct product), where P is defined as above.
The two most important examples covered by this are when:
- G is a compact connected semisimple Lie group with τ a period two automorphism;
- G is a semidirect product
, with A a locally compact Abelian group without 2-torsion and τ(a· k)= k·a−1 for a in A and k in K.
The three cases cover the three types of symmetric space
Symmetric space
A symmetric space is, in differential geometry and representation theory, a smooth manifold whose group of symmetries contains an "inversion symmetry" about every point...
s G/K:
- Non-compact type, when K is a maximal compact subgroup of a non-compact real semisimple Lie group G;
- Compact type, when K is the fixed point subgroup of a period two automorphism of a compact semisimple Lie group G;
- Euclidean type, when A is a finite-dimensional Euclidean space with an orthogonal action of K.
Cartan–Helgason theorem
Let G be a compact semisimple connected and simply connected Lie group and τ a period two automorphism of a G with fixed point subgroup K = Gτ. In this case K is a connected compact Lie group. In addition let T be a maximal torusMaximal torus
In the mathematical theory of compact Lie groups a special role is played by torus subgroups, in particular by the maximal torus subgroups.A torus in a Lie group G is a compact, connected, abelian Lie subgroup of G . A maximal torus is one which is maximal among such subgroups...
of G invariant under τ, such that T
P is a maximal torus in P, and set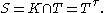S is the direct product of a torus and an elementary abelian 2-group
Elementary Abelian group
In group theory, an elementary abelian group is a finite abelian group, where every nontrivial element has order p, where p is a prime; in particular it is a p-group....
.
In 1929 Élie Cartan
Élie Cartan
Élie Joseph Cartan was an influential French mathematician, who did fundamental work in the theory of Lie groups and their geometric applications...
found a rule to determine the decomposition of L2(G/K) into the direct sum of finite-dimensional irreducible representations of G, which was proved rigorously only in 1970 by Sigurdur Helgason
Sigurdur Helgason (mathematician)
Sigurdur Helgason is an Icelandic-American mathematician specializing in integral geometry and its generalizations to symmetric spaces. He was born in Akureyri, Iceland. Since 1965, he has been a professor of mathematics at the Massachusetts Institute of Technology. He was winner of the 1988...
. Because the commutant of G on L2(G/K) is commutative, each irreducible representation appears with multiplicity one. By Frobenius reciprocity for compact groups, the irreducible representations V that occur are precisely those admitting a non-zero vector fixed by K.
From the representation theory of compact semisimple groups
Weyl character formula
In mathematics, the Weyl character formula in representation theory describes the characters of irreducible representations of compact Lie groups in terms of their highest weights. It was proved by ....
, irreducible representations of G are classified by their highest weight
Root system
In mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras...
. This is specified by a homomorphism of the maximal torus T into T.
The Cartan–Helgason theorem states that
| the irreducible representations of G admitting a non-zero vector fixed by K are precisely those with highest weights corresponding to homomorphisms trivial on S. |
The corresponding irreducible representations are called spherical representations.
The theorem can be proved using the Iwasawa decomposition
Iwasawa decomposition
In mathematics, the Iwasawa decomposition KAN of a semisimple Lie group generalises the way a square real matrix can be written as a product of an orthogonal matrix and an upper triangular matrix...
:
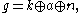
where
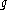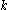, , are the complexifications of the Lie algebraLie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
s of G, K, A = T
P andsummed over all eigenspaces for T in
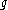corresponding to positive rootsRoot system
In mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras...
α not fixed by τ.
Let V be a spherical representation with highest weight vector v0 and K-fixed vector vK. Since v0 is an eigenvector of the solvable Lie algebra
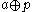, the Poincaré–Birkhoff–Witt theoremPoincaré–Birkhoff–Witt theorem
In the theory of Lie algebras, the Poincaré–Birkhoff–Witt theorem is a result giving an explicit description of the universal enveloping algebra of a Lie algebra...
implies that the K-module generated by v0 is the whole of V. If Q is the orthogonal projection onto the fixed points of K in V obtained by averaging over G with respect to Haar measure
Haar measure
In mathematical analysis, the Haar measure is a way to assign an "invariant volume" to subsets of locally compact topological groups and subsequently define an integral for functions on those groups....
, it follows that
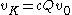
for some non-zero constant c. Because vK is fixed by S and v0 is an eigenvector for S, the subgroup S must actually fix v0, an equivalent form of the triviality condition on S.
Conversely if v0 is fixed by S, then it can be shown that the matrix coefficient
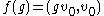
is non-negative on K. Since f(1) > 0, it follows that (Qv0, v0) > 0 and hence that Qv0 is a non-zero vector fixed by K.
Harish-Chandra's formula
If G is a non-compact semisimple Lie group, its maximal compact subgroup K acts by conjugation on the component P in the Cartan decompositionCartan decomposition
The Cartan decomposition is a decomposition of a semisimple Lie group or Lie algebra, which plays an important role in their structure theory and representation theory. It generalizes the polar decomposition of matrices.- Cartan involutions on Lie algebras :...
. If A is a maximal Abelian subgroup of G contained in P, then A is isomorphic to its Lie algebra under the exponential map and, as a further generalisation
Lie group decompositions
In mathematics, Lie group decompositions, named after Sophus Lie, are used to analyse the structure of Lie groups and associated objects, by showing how they are built up out of subgroups. They are essential technical tools in the representation theory of Lie groups and Lie algebras; they can also...
of the polar decomposition of matrices, every element of P is conjugate under K to an element of A, so that
- G =KAK.
There is also an associated Iwasawa decomposition
Iwasawa decomposition
In mathematics, the Iwasawa decomposition KAN of a semisimple Lie group generalises the way a square real matrix can be written as a product of an orthogonal matrix and an upper triangular matrix...
- G =KAN,
where N is a closed nilpotent subgroup, diffeomorphic to its Lie algebra under the exponential map and normalised by A. Thus
S=AN is a closed solvable subgroup
Solvable group
In mathematics, more specifically in the field of group theory, a solvable group is a group that can be constructed from abelian groups using extensions...
of G, the semidirect product
Semidirect product
In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
of N by A, and G = KS.
If α in Hom(A,T) is a character
Character (mathematics)
In mathematics, a character is a special kind of function from a group to a field . There are at least two distinct, but overlapping meanings...
of A, then α extends to a character of S, by defining it to be trivial on N. There is a corresponding unitary
Unitary representation
In mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
induced representation
Induced representation
In mathematics, and in particular group representation theory, the induced representation is one of the major general operations for passing from a representation of a subgroup H to a representation of the group G itself. It was initially defined as a construction by Frobenius, for linear...
σ of G on L2(G/S) = L2(K), a so-called (spherical) principal series representation
Principal series representation
In mathematics, the principal series representations of certain kinds of topological group G occur in the case where G is not a compact group. There, by analogy with spectral theory, one expects that the regular representation of G will decompose according to some kind of continuous spectrum, of...
.
This representation can be described explicitly as follows. Unlike G and K, the solvable Lie group S is not unimodular. Let dx denote left invariant Haar measure on S and ΔS the modular function of S. Then
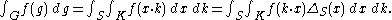
The principal series representation σ is realised on L2(K) as
where
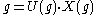
is the Iwasawa decomposition of g with U(g) in K and X(g) in S and
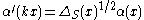
for k in K and x in S.
The representation σ is irreducible, so that if v denotes the constant function 1 on K, fixed by K,
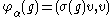
defines a zonal spherical function of G.
Computing the inner product above leads to Harish-Chandra's formula for the zonal spherical function
 |
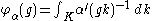as an integral over K.
Harish-Chandra proved that these zonal spherical functions exhaust the characters of the C* algebra generated by the Cc(K \ G / K) acting by right convolution on L2(G / K). He also showed that two different characters α and β give the same zonal spherical function if and only if α = β·s, where s is in the Weyl group
Weyl group
In mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection...
of A
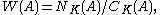
the quotient of the normaliser of A in K by its centraliser, a finite reflection group.
It can also be verified directly that this formula defines a zonal spherical function, without using representation theory. The proof for general semisimple Lie groups that every zonal spherical formula arises in this way requires the detailed study of G-invariant differential operators on G/K and their simultaneous eigenfunctions (see below). In the case of complex semisimple groups, Harish-Chandra and Felix Berezin
Felix Berezin
Felix Alexandrovich Berezin was a Soviet Russian mathematician and physicist known for his contributions to the theory of supersymmetry and supermanifolds as well as to the path integral formulation of quantum field theory....
realised independently that the formula simplified considerably and could be proved more directly.
The remaining positive-definite zonal spherical functions are given
by Harish-Chandra's formula with α in Hom(A,C*) instead of Hom(A,T). Only certain α are permitted and the corresponding irreducible
representations arise as analytic continuations of the spherical principal series. This so-called "complementary series" was first studied by for G = SL(2,R) and by and for G = SL(2,C).
Subsequently in the 1960s, the construction of a complementary series by analytic continuation of the spherical principal series was systematically developed for general semisimple Lie groups by Ray Kunze, Elias Stein and Bertram Kostant
Bertram Kostant
-Early life and education:Kostant grew up in New York City, where he graduated from the celebrated Stuyvesant High School in 1945. He went on to obtain an undergraduate degree in mathematics from Purdue University in 1950. He earned his Ph.D...
. Since these irreducible representations are not tempered
Tempered representation
In mathematics, a tempered representation of a linear semisimple Lie group is a representation that has a basis whose matrix coefficients lie in the Lp spacefor any ε > 0.-Formulation:...
, they are not usually required for harmonic analysis on G (or G / K).
Eigenfunctions
Harish-Chandra proved that zonal spherical functions can be characterised as those normalised positive definite K-invariant functions on G/K that are eigenfunctions of D(G/K), the algebra of invariant differential operators on G. This algebra acts on G/K and commutes with the natural action of G by left translation. It can be identified with the subalgebra of the universal enveloping algebraUniversal enveloping algebra
In mathematics, for any Lie algebra L one can construct its universal enveloping algebra U. This construction passes from the non-associative structure L to a unital associative algebra which captures the important properties of L.Any associative algebra A over the field K becomes a Lie algebra...
of G fixed under the adjoint action of K. As for the commutant of G on L2(G/K) and the corresponding Hecke algebra, this algebra of operators is commutative; indeed it is a subalgebra of the algebra of mesurable operators
Affiliated operator
In mathematics, affiliated operators were introduced by Murray and von Neumann in the theory of von Neumann algebras as a technique for using unbounded operators to study modules generated by a single vector...
affiliated with the commutant π(G)', an Abelian von Neumann algebra. As Harish-Chandra proved, it is isomorphic to the algebra of W(A)-invariant polynomials on the Lie algebra of A, which itself is a polynomial ring
Polynomial ring
In mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
by the Chevalley–Shephard–Todd theorem
Chevalley–Shephard–Todd theorem
In mathematics, the Chevalley–Shephard–Todd theorem in invariant theory of finite groups states that the ring of invariants of a finite group acting on a complex vector space is a polynomial ring if and only if the group is generated by pseudoreflections. In the case of subgroups of the complex...
on polynomial invariants of finite reflection groups. The simplest invariant differential operator on G/K is the Laplacian operator; up to a sign this operator is just the image under π of the Casimir operator in the centre of the universal enveloping algebra of G.
Thus a normalised positive definite K-biinvariant function f on G is a zonal spherical function if and only if for each D in D(G/K) there is a constant λD such that
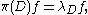
i.e. f is a simultaneous eigenfunction
Eigenfunction
In mathematics, an eigenfunction of a linear operator, A, defined on some function space is any non-zero function f in that space that returns from the operator exactly as is, except for a multiplicative scaling factor. More precisely, one has...
of the operators π(D).
If ψ is a zonal spherical function, then, regarded as a function on G/K, it is an eigenfunction of the Laplacian
there, an elliptic differential operator with real analytic coefficients. By analytic elliptic regularity,
ψ is a real analytic function on G/K, and hence G.
Harish-Chandra used these facts about the structure of the invariant operators to prove that his formula gave all zonal spherical functions for real semisimple Lie groups. Indeed the commutativity of the commutant implies that the simultaneous eigenspaces of the algebra of invariant differential operators all have dimension one; and the polynomial structure of this algebra forces the simultaneous eigenvalues to be precisely those already associated with Harish-Chandra's formula.
Example: SL(2,C)
The group G = SL(2,C) is the complexificationComplexification
In mathematics, the complexification of a real vector space V is a vector space VC over the complex number field obtained by formally extending scalar multiplication to include multiplication by complex numbers. Any basis for V over the real numbers serves as a basis for VC over the complex...
of the compact Lie group K = SU(2) and the double cover of the Lorentz group
Lorentz group
In physics , the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical setting for all physical phenomena...
. The infinite-dimensional representations of the Lorentz group were first studied by Dirac
Paul Dirac
Paul Adrien Maurice Dirac, OM, FRS was an English theoretical physicist who made fundamental contributions to the early development of both quantum mechanics and quantum electrodynamics...
in 1945, who considered the discrete series representations, which he termed expansors. A systematic study was taken up shortly afterwards by Harish-Chandra, Gelfand–Naimark and
Bargmann. The irreducible representations of class one, corresponding to the zonal spherical functions, can be determined easily using the radial
component of the Laplacian operator.
Indeed any unimodular complex 2×2 matrix g admits a unique polar decomposition g = pv with v unitary and p positive. In turn
p = uau*, with u unitary and a a diagonal matrix with positive entries. Thus g = uaw with w = u* v, so that any K-biinvariant function on G corresponds to a function of the diagonal matrix
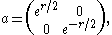
invariant under the Weyl group. Identifying G/K with hyperbolic 3-space, the zonal hyperbolic functions ψ correspond to radial functions that are eigenfunctions of the Laplacian. But in terms of the radial coordinate r, the Laplacian is given by
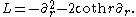
Setting f(r) = sinh (r)·ψ(r), it follows that f is an odd function of r and an eigenfunction of
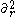.Hence
 |
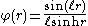where
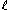is real.There is a similar elementary treatment for the generalized Lorentz groups SO(N,1) in and (recall that SO0(3,1) = SL(2,C) / ±I).
Complex case
If G is a complex semisimple Lie group, it is the complexificationComplexification
In mathematics, the complexification of a real vector space V is a vector space VC over the complex number field obtained by formally extending scalar multiplication to include multiplication by complex numbers. Any basis for V over the real numbers serves as a basis for VC over the complex...
of its maximal compact subgroup K. If
and 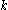are their Lie algebras, then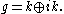Let T be a maximal torus
Maximal torus
In the mathematical theory of compact Lie groups a special role is played by torus subgroups, in particular by the maximal torus subgroups.A torus in a Lie group G is a compact, connected, abelian Lie subgroup of G . A maximal torus is one which is maximal among such subgroups...
in K with Lie algebra
. Then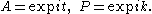Let
be the Weyl group
Weyl group
In mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection...
of T in K. Recall characters
in Hom(T,T) are called weights
Weight (representation theory)
In the mathematical field of representation theory, a weight of an algebra A over a field F is an algebra homomorphism from A to F – a linear functional – or equivalently, a one dimensional representation of A over F. It is the algebra analogue of a multiplicative character of a group...
and
can be identified with elements of the weight lattice Λ in
Hom(
, R) = 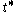.There is a natural ordering on weights and very finite-dimensional
irreducible representation (π, V) of K has a unique highest weight
λ. The weights of the adjoint representation
Adjoint representation
In mathematics, the adjoint representation of a Lie group G is the natural representation of G on its own Lie algebra...
of K
on
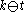are called rootsand ρ is used to denote half the sum of the positive roots α,
Weyl's character formula asserts that for z = exp X in T
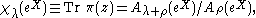
where, for μ in
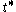, Aμ denotes the antisymmetrisationand ε denotes the sign character of the finite reflection group W.
Weyl's denominator formula expresses the denominator Aρ as a product:
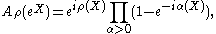
where the product is over the positive roots.
Weyl's dimension formula asserts that
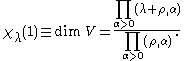
where the inner product on
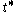is that associated with the Killing formKilling form
In mathematics, the Killing form, named after Wilhelm Killing, is a symmetric bilinear form that plays a basic role in the theories of Lie groups and Lie algebras...
on
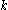.Now
- every irreducible representation of K extends holomorphically to the complexification G
- every irreducible character χλ(k) of K extends holomorphically to the complexification of K and
.
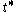- for every λ in Hom(A,T) =
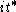, there is a zonal spherical function φλ.
The Berezin–Harish–Chandra formula asserts that for X in
 |
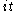
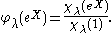In other words:
- the zonal spherical functions on a complex semisimple Lie group are given by analytic continuation of the formula for the normalised characters.
One of the simplest proofs of this formula involves the radial component on A of the Laplacian on G, a proof formally parallel to Helgason's reworking of Freudenthal
Freudenthal
Freudenthal is a surname and may refer to:* Axel Olof Freudenthal , a Finland-Swedish philologist and politician* Dave Freudenthal, a U.S...
's classical proof of the Weyl character formula
Weyl character formula
In mathematics, the Weyl character formula in representation theory describes the characters of irreducible representations of compact Lie groups in terms of their highest weights. It was proved by ....
, using the radial component on T of the Laplacian on K.
In the latter case the class function
Class function
In mathematics, especially in the fields of group theory and representation theory of groups, a class function is a function f on a group G, such that f is constant on the conjugacy classes of G. In other words, f is invariant under the conjugation map on G...
s on K can be identified with W-invariant functions on T. The
radial component of ΔK on T is just the expression for the restriction of ΔK to W-invariant functions on T, where
it is given by the formula
where
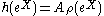
for X in
. If χ is a character with highest weight λ, it follows that φ = h·χ satisfies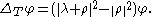Thus for every weight μ with non-zero Fourier coefficient in φ,
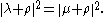
The classical argument of Freudenthal shows that μ + ρ must have the form s(λ + ρ) for some s in W, so the character formula
follows from the antisymmetry of φ.
Similarly K-biinvariant functions on G can be identified with W(A)-invariant functions on A. The
radial component of ΔG on A is just the expression for the restriction of ΔG to W(A)-invariant functions on A.
It is given by the formula
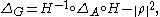
where
for X in
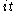.The Berezin–Harish–Chandra formula for a zonal spherical function φ can be established by introducing the antisymmetric function
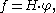
which is an eigenfunction of the Laplacian ΔA. Since K is generated by copies of subgroups that are homomorphic images of SU(2) corresponding to simple root
Simple root
in mathematics the term simple root can refer to one of two unrelated notions:*A simple root of a polynomial is a root of multiplicity one*A simple root in a root system is a member of a subset determined by a choice of positive roots...
s, its complexification G is generated by the corresponding homomorphic images of SL(2,C). The formula for zonal spherical functions of SL(2,C) implies that f is a periodic function
Periodic function
In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
on
with respect to some sublatticeLattice (discrete subgroup)
In Lie theory and related areas of mathematics, a lattice in a locally compact topological group is a discrete subgroup with the property that the quotient space has finite invariant measure...
. Antisymmetry under the Weyl group and the argument of Freudenthal again imply that ψ must have the stated form up to a multiplicative constant, which can be determined using the Weyl dimension formula.
Example: SL(2,R)
The theory of zonal spherical functions for SL(2,R) originated in the work of Mehler in 1881 on hyperbolic geometry. He discovered the analogue of the Plancherel theorem, which was rediscovered by Fock in 1943. The corresponding eigenfunction expansion is termed the Mehler–Fock transform. It was already put on a firm footing in 1910 by Hermann WeylHermann Weyl
Hermann Klaus Hugo Weyl was a German mathematician and theoretical physicist. Although much of his working life was spent in Zürich, Switzerland and then Princeton, he is associated with the University of Göttingen tradition of mathematics, represented by David Hilbert and Hermann Minkowski.His...
's important work on the spectral theory of ordinary differential equations
Spectral theory of ordinary differential equations
In mathematics, the spectral theory of ordinary differential equations is the part of spectral theory concerned with the determination of the spectrum and eigenfunction expansion associated with a linear ordinary differential equation...
. The radial part of the Laplacian in this case leads to a hypergeometric differential equation
Hypergeometric differential equation
In mathematics, the Gaussian or ordinary hypergeometric function 2F1 is a special function represented by the hypergeometric series, that includes many other special functions as specific or limiting cases. It is a solution of a second-order linear ordinary differential equation...
, the theory of which was treated in detail by Weyl. Weyl's approach was subsequently generalised by Harish-Chandra to study zonal spherical functions and the corresponding Plancherel theorem for more general semimisimple Lie groups. Following the work of Dirac on the discrete series representations of SL(2,R), the general theory of unitary irreducible representations of SL(2,R) was developed independently by Bargmann, Harish-Chandra and Gelfand–Naimark. The irreducible representations of class one, or equivalently the theory of zonal spherical functions, form an important special case of this theory.
The group G = SL(2,R) is a double cover of the 3-dimensional Lorentz group
Lorentz group
In physics , the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical setting for all physical phenomena...
SO(2,1), the symmetry group
Symmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
of the hyperbolic plane
Hyperbolic space
In mathematics, hyperbolic space is a type of non-Euclidean geometry. Whereas spherical geometry has a constant positive curvature, hyperbolic geometry has a negative curvature: every point in hyperbolic space is a saddle point...
with its Poincaré metric
Poincaré metric
In mathematics, the Poincaré metric, named after Henri Poincaré, is the metric tensor describing a two-dimensional surface of constant negative curvature. It is the natural metric commonly used in a variety of calculations in hyperbolic geometry or Riemann surfaces.There are three equivalent...
. It acts by Moebius transformations. The upper half-plane can be identified with the unit disc by the Cayley transform
Cayley transform
In mathematics, the Cayley transform, named after Arthur Cayley, has a cluster of related meanings. As originally described by , the Cayley transform is a mapping between skew-symmetric matrices and special orthogonal matrices. In complex analysis, the Cayley transform is a conformal mapping in...
. Under this identification G becomes identified with the group SU(1,1), also acting by Moebius transformations. Because the action is
transitive, both spaces can be identified with G/K, where K = SO(2). The metric is invariant under G and the associated Laplacian is G-invariant, coinciding with the image of the Casimir operator. In the upper half-plane model the Laplacian is given by the formula
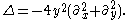
If s is a complex number and z = x + i y with y > 0, the function
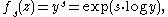
is an eigenfunction of Δ:
Since Δ commutes with G, any left translate of fs is also an eigenfunction with the same eigenvalue. In particular, averaging over K, the function
 |
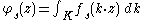is a K-invariant eigenfunction of Δ on G/K. When
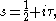
with τ real, these functions give all the zonal spherical functions on G. As with Harish-Chandra's more general formula for semisimple Lie groups, φs is a zonal spherical function because it is the matrix coefficient corresponding to a vector fixed by K in the principal series. Various arguments are available to prove that there are no others. One of the simplest classical Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
ic arguments is to note that, since Δ is an elliptic operator with analytic coefficients, by analytic elliptic regularity any eigenfunction is necessarily real analytic.
Hence, if the zonal spherical function corresponds is the matrix coefficient for a vector v and representation σ, the vector v is an analytic vector
Unitary representation
In mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
for G and
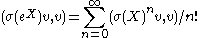
for X in
. The infinitesimal form of the irreducible unitary representations with a vector fixed by K were worked out classically by Bargmann. They correspond precisely to the principal series of SL(2,R). It follows that the zonal spherical function corresponds to a principal series representation.Another classical argument proceeds by showing that on radial functions the Laplacian has the form
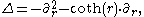
so that, as a function of r, the zonal spherical function φ(r) must satisfy the ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
for some constant α. The change of variables t = sinh r transforms this equation into the hypergeometric differential equation
Hypergeometric differential equation
In mathematics, the Gaussian or ordinary hypergeometric function 2F1 is a special function represented by the hypergeometric series, that includes many other special functions as specific or limiting cases. It is a solution of a second-order linear ordinary differential equation...
. The general solution in terms of Legendre functions of complex index is given by
 |
where α = ρ(ρ+1). Further restrictions on ρ are imposed by boundedness and positive-definiteness of the zonal spherical function on G.
There is yet another approach, due to Mogens Flensted-Jensen, which derives the properties of the zonal spherical functions on SL(2,R),
including the Plancherel formula, from the corresponding results for SL(2,C), which are simple consequences of the Plancherel formula and Fourier inversion formula for R. This "method of descent" works more generally, allowing results for a real semisimple Lie group to be derived by descent from the corresponding results for its complexification.
Further directions
- The theory of zonal functions that are not necessarily positive-definite. These are given by the same formulas as above, but without restrictions on the complex parameter s or ρ. They correspond to non-unitary representations.
- Harish-Chandra's eigenfunction expansion and inversion formula for spherical functionsPlancherel theorem for spherical functionsIn mathematics, the Plancherel theorem for spherical functions is an important result in the representation theory of semisimple Lie groups, due in its final form to Harish-Chandra...
. This is an important special case of his Plancherel theoremPlancherel theoremIn mathematics, the Plancherel theorem is a result in harmonic analysis, proved by Michel Plancherel in 1910. It states that the integral of a function's squared modulus is equal to the integral of the squared modulus of its frequency spectrum....
for real semisimple Lie groups. - The structure of the Hecke algebra. Harish-Chandra and Godement proved that, as convolution algebras, there are natural isomorphisms between Cc∞(K \ G / K ) and Cc∞(A)W, the subalgebra invariant under the Weyl group. This is straightforward to establish for SL(2,R).
- Spherical functions for Euclidean motion groupsEuclidean groupIn mathematics, the Euclidean group E, sometimes called ISO or similar, is the symmetry group of n-dimensional Euclidean space...
and compact Lie groups. - Spherical functions for p-adic Lie groups. These were studied in depth by Satake and MacdonaldIan G. MacdonaldIan Grant Macdonald is a British mathematician known for his contributions to symmetric functions, special functions, Lie algebra theory and other aspects of algebraic combinatorics ....
. Their study, and that of the associated Hecke algebras, was one of the first steps in the extensive representation theory of semisimple p-adic Lie groups, a key element in the Langlands programLanglands programThe Langlands program is a web of far-reaching and influential conjectures that relate Galois groups in algebraic number theory to automorphic forms and representation theory of algebraic groups over local fields and adeles. It was proposed by ....
.
See also
- Plancherel theorem for spherical functionsPlancherel theorem for spherical functionsIn mathematics, the Plancherel theorem for spherical functions is an important result in the representation theory of semisimple Lie groups, due in its final form to Harish-Chandra...
- Hecke algebra of a locally compact group
- Representations of Lie groups
- Non-commutative harmonic analysis
- Tempered representationTempered representationIn mathematics, a tempered representation of a linear semisimple Lie group is a representation that has a basis whose matrix coefficients lie in the Lp spacefor any ε > 0.-Formulation:...
- Positive definite function on a groupPositive definite function on a groupIn operator theory, a positive-definite function on a group relates the notions of positivity, in the context of Hilbert spaces, and algebraic groups...
- Symmetric spaceSymmetric spaceA symmetric space is, in differential geometry and representation theory, a smooth manifold whose group of symmetries contains an "inversion symmetry" about every point...
- Gelfand pairGelfand pairIn mathematics, the expression Gelfand pair is a pair consisting of a group G and a subgroup K that satisfies a certain property on restricted representations. The theory of Gelfand pairs is closely related to the topic of spherical functions in the classical theory of special functions, and to...