
Plancherel measure
Encyclopedia
In mathematics
, Plancherel measure is a probability measure
defined on the set of irreducible representations of a finite group
 . In some cases the term Plancherel measure is applied specifically in the context of the group
. In some cases the term Plancherel measure is applied specifically in the context of the group  being the finite symmetric group
being the finite symmetric group 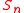 – see below. It is named after the Swiss mathematician Michel Plancherel
– see below. It is named after the Swiss mathematician Michel Plancherel
for his work in representation theory
.
 be a finite group
be a finite group
, we denote the set of its irreducible representations by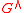 . The corresponding Plancherel measure over the set
. The corresponding Plancherel measure over the set 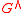 is defined by
is defined by
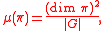
where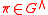 , and
, and  denotes the dimension of the irreducible representation
denotes the dimension of the irreducible representation  .
.
Definition on the symmetric group
An important special case is the case of the finite symmetric group
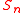 , where
, where  is a positive integer. For this group, the set
is a positive integer. For this group, the set  of irreducible representations is in natural bijection with the set of integer partitions of
of irreducible representations is in natural bijection with the set of integer partitions of  . For an irreducible representation associated with an integer partition
. For an irreducible representation associated with an integer partition  , its dimension is known to be equal to
, its dimension is known to be equal to 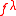 , the number of standard Young tableaux of shape
, the number of standard Young tableaux of shape  , so in this case Plancherel measure is often thought of as a measure on the set of integer partitions of given order n, given by
, so in this case Plancherel measure is often thought of as a measure on the set of integer partitions of given order n, given by
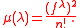
The fact that those probabilities sum up to 1 follows from the combinatorial identity
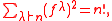
which corresponds to the bijective nature of the Robinson–Schensted correspondence.
of a random permutation
 . As a result of its importance in that area, in many current research papers the term Plancherel measure almost exclusively refers to the case of the symmetric group
. As a result of its importance in that area, in many current research papers the term Plancherel measure almost exclusively refers to the case of the symmetric group  .
.
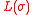 denote the length of a longest increasing subsequence of a random permutation
denote the length of a longest increasing subsequence of a random permutation
 in
in 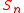 chosen according to the uniform distribution. Let
chosen according to the uniform distribution. Let  denote the shape of the corresponding Young tableau
denote the shape of the corresponding Young tableau
x related to by the Robinson–Schensted correspondence. Then the following identity holds:
by the Robinson–Schensted correspondence. Then the following identity holds:
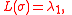
where denotes the length of the first row of
denotes the length of the first row of  . Furthermore, from the fact that the Robinson–Schensted correspondence is bijective it follows that the distribution of
. Furthermore, from the fact that the Robinson–Schensted correspondence is bijective it follows that the distribution of  is exactly the Plancherel measure on
is exactly the Plancherel measure on  . So, to understand the behavior of
. So, to understand the behavior of 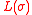 , it is natural to look at
, it is natural to look at  with
with  chosen according to the Plancherel measure in
chosen according to the Plancherel measure in 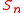 , since these two random variables have the same probability distribution.
, since these two random variables have the same probability distribution.
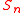 for each integer
for each integer  . In various studies of the asymptotic behavior of
. In various studies of the asymptotic behavior of 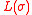 as
as  , it has proved useful to extend the measure to a measure, called the Poissonized Plancherel measure, on the set
, it has proved useful to extend the measure to a measure, called the Poissonized Plancherel measure, on the set  of all integer partitions. For any
of all integer partitions. For any  , the Poissonized Plancherel measure with parameter
, the Poissonized Plancherel measure with parameter  on the set
on the set  is defined by
is defined by
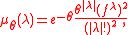
for all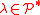 .
.
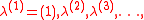 such that each
such that each 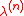 is a random Young diagram of order
is a random Young diagram of order  whose probability distribution is the nth Plancherel measure, and each successive
whose probability distribution is the nth Plancherel measure, and each successive  is obtained from its predecessor
is obtained from its predecessor 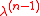 by the addition of a single box, according to the transition probability
by the addition of a single box, according to the transition probability

for any given Young diagrams and
and  of sizes n − 1 and n, respectively.
of sizes n − 1 and n, respectively.
So, the Plancherel growth process can be viewed as a natural coupling of the different Plancherel measures of all the symmetric groups, or alternatively as a random walk
on Young's lattice
. It is not difficult to show that the probability distribution
of in this walk coincides with the Plancherel measure on
in this walk coincides with the Plancherel measure on 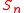 .
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Plancherel measure is a probability measure
Probability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
defined on the set of irreducible representations of a finite group
Finite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
 . In some cases the term Plancherel measure is applied specifically in the context of the group
. In some cases the term Plancherel measure is applied specifically in the context of the group  being the finite symmetric group
being the finite symmetric group 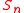 – see below. It is named after the Swiss mathematician Michel Plancherel
– see below. It is named after the Swiss mathematician Michel PlancherelMichel Plancherel
Michel Plancherel was a Swiss mathematician. He was born in Bussy and obtained his diploma in mathematics from the University of Fribourg in 1907...
for his work in representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
.
General definition
Let be a finite group
be a finite groupFinite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
, we denote the set of its irreducible representations by
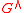 . The corresponding Plancherel measure over the set
. The corresponding Plancherel measure over the set 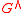 is defined by
is defined by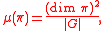
where
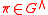 , and
, and  denotes the dimension of the irreducible representation
denotes the dimension of the irreducible representation  .
. Definition on the symmetric group 
An important special case is the case of the finite symmetric groupSymmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
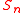 , where
, where  is a positive integer. For this group, the set
is a positive integer. For this group, the set  of irreducible representations is in natural bijection with the set of integer partitions of
of irreducible representations is in natural bijection with the set of integer partitions of  . For an irreducible representation associated with an integer partition
. For an irreducible representation associated with an integer partition  , its dimension is known to be equal to
, its dimension is known to be equal to 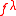 , the number of standard Young tableaux of shape
, the number of standard Young tableaux of shape  , so in this case Plancherel measure is often thought of as a measure on the set of integer partitions of given order n, given by
, so in this case Plancherel measure is often thought of as a measure on the set of integer partitions of given order n, given by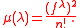
The fact that those probabilities sum up to 1 follows from the combinatorial identity
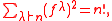
which corresponds to the bijective nature of the Robinson–Schensted correspondence.
Application
Plancherel measure appears naturally in combinatorial and probabilistic problems, especially in the study of longest increasing subsequenceLongest increasing subsequence
The longest increasing subsequence problem is to find a subsequence of a given sequence in which the subsequence elements are in sorted order, lowest to highest, and in which the subsequence is as long as possible...
of a random permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
 . As a result of its importance in that area, in many current research papers the term Plancherel measure almost exclusively refers to the case of the symmetric group
. As a result of its importance in that area, in many current research papers the term Plancherel measure almost exclusively refers to the case of the symmetric group  .
.Connection to longest increasing subsequence
Let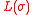 denote the length of a longest increasing subsequence of a random permutation
denote the length of a longest increasing subsequence of a random permutationPermutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
 in
in 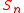 chosen according to the uniform distribution. Let
chosen according to the uniform distribution. Let  denote the shape of the corresponding Young tableau
denote the shape of the corresponding Young tableauYoung tableau
In mathematics, a Young tableau is a combinatorial object useful in representation theory. It provides a convenient way to describe the group representations of the symmetric and general linear groups and to study their properties. Young tableaux were introduced by Alfred Young, a mathematician at...
x related to
 by the Robinson–Schensted correspondence. Then the following identity holds:
by the Robinson–Schensted correspondence. Then the following identity holds: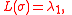
where
 denotes the length of the first row of
denotes the length of the first row of  . Furthermore, from the fact that the Robinson–Schensted correspondence is bijective it follows that the distribution of
. Furthermore, from the fact that the Robinson–Schensted correspondence is bijective it follows that the distribution of  is exactly the Plancherel measure on
is exactly the Plancherel measure on  . So, to understand the behavior of
. So, to understand the behavior of 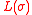 , it is natural to look at
, it is natural to look at  with
with  chosen according to the Plancherel measure in
chosen according to the Plancherel measure in 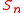 , since these two random variables have the same probability distribution.
, since these two random variables have the same probability distribution. Poissonized Plancherel measure
Plancherel measure is defined on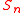 for each integer
for each integer  . In various studies of the asymptotic behavior of
. In various studies of the asymptotic behavior of 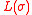 as
as  , it has proved useful to extend the measure to a measure, called the Poissonized Plancherel measure, on the set
, it has proved useful to extend the measure to a measure, called the Poissonized Plancherel measure, on the set  of all integer partitions. For any
of all integer partitions. For any  , the Poissonized Plancherel measure with parameter
, the Poissonized Plancherel measure with parameter  on the set
on the set  is defined by
is defined by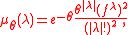
for all
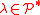 .
. Plancherel growth process
The Plancherel growth process is a random sequence of Young diagrams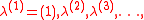 such that each
such that each 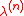 is a random Young diagram of order
is a random Young diagram of order  whose probability distribution is the nth Plancherel measure, and each successive
whose probability distribution is the nth Plancherel measure, and each successive  is obtained from its predecessor
is obtained from its predecessor 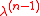 by the addition of a single box, according to the transition probability
by the addition of a single box, according to the transition probability
for any given Young diagrams
 and
and  of sizes n − 1 and n, respectively.
of sizes n − 1 and n, respectively. So, the Plancherel growth process can be viewed as a natural coupling of the different Plancherel measures of all the symmetric groups, or alternatively as a random walk
Random walk
A random walk, sometimes denoted RW, is a mathematical formalisation of a trajectory that consists of taking successive random steps. For example, the path traced by a molecule as it travels in a liquid or a gas, the search path of a foraging animal, the price of a fluctuating stock and the...
on Young's lattice
Young's lattice
In mathematics, Young's lattice is a partially ordered set and a lattice that is formed by all integer partitions. It is named after Alfred Young, who in a series of papers On quantitative substitutional analysis developed representation theory of the symmetric group...
. It is not difficult to show that the probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
of
 in this walk coincides with the Plancherel measure on
in this walk coincides with the Plancherel measure on 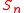 .
.

