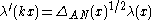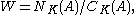Plancherel theorem for spherical functions
Encyclopedia
In mathematics
, the Plancherel theorem for spherical functions is an important result in the representation theory
of semisimple Lie groups, due in its final form to Harish-Chandra
. It is a natural generalisation in non-commutative harmonic analysis of the Plancherel formula and Fourier inversion formula in the representation theory of the group of real numbers in classical harmonic analysis
and has a similarly close interconnection with the theory of differential equation
s.
It is the special case for zonal spherical function
s of the general Plancherel theorem
for semisimple Lie groups, also proved by Harish-Chandra. The Plancherel theorem gives the eigenfunction expansion
of radial functions for the Laplacian operator on the associated symmetric space
X; it also gives the direct integral decomposition
into irreducible representations of the regular representation
on L2(X). In the case of
hyperbolic space
, these expansions were known from prior results of Mehler, Weyl and Fock
.
The main reference for almost all this material is the encyclopedic text of .
locally compact group
G were due to Segal and Mautner. At around the same time, Harish-Chandra and Gelfand & Naimark derived an explicit formula for SL(2,R) and complex semisimple Lie groups, so in particular the Lorentz group
s. A simpler abstract formula was derived by Mautner for a "topological" symmetric space G/K corresponding to a maximal compact subgroup
K. Godement
gave a more concrete and satisfactory form for positive definite
spherical functions
, a class of special functions on G/K. Since when G is a semisimple Lie group these spherical functions φλ were naturally labelled by a parameter λ in the quotient of a Euclidean space
by the action of a finite reflection group, it became a central problem to determine explicitly the Plancherel measure
in terms of this parametrization. Generalizing the ideas of Hermann Weyl
from the spectral theory of ordinary differential equations
, Harish-Chandra introduced his celebrated c-function c(λ) to describe the asymptotic behaviour of the spherical functions φλ and proposed c(λ)−2 dλ as the Plancherel measure. He verified this formula for the special cases when G is complex or real rank
one, thus in particular covering the case when G/K is a hyperbolic space
. The general case was reduced to two conjectures about the properties of the c-function and the so-called spherical Fourier transform. Explicit formulas for the c-function were later obtained for a large class of classical semisimple Lie groups by Bhanu-Murthy. In turn these formulas prompted Gindikin and Karpelevič to derive a product formula for the c-function, reducing the computation to Harish-Chandra's formula for the rank 1 case. Their work finally enabled Harish-Chandra to complete his proof of the Plancherel theorem for spherical functions in 1966.
In many special cases, for example for complex semisimple group or the Lorentz groups, there are simple methods to develop the theory directly. Certain subgroups of these groups can be treated by techniques generalising the well-known "method of descent" due to Jacques Hadamard
. In particular gave a general method for deducing properties of the spherical transform for a real semisimple group from that of its complexification.
One of the principal applications and motivations for the spherical transform was Selberg's trace formula. The classical Poisson summation formula
combines the Fourier inversion formula on a vector group with summation over a cocompact lattice. In Selberg's analogue of this formula, the vector group is replaced by G/K, the Fourier transform by the spherical transform and the lattice by a cocompact (or cofinite) discrete subgroup. The original paper of implicitly invokes the spherical transform; it was who brought the transform to the fore, giving in particular an elementary treatment for SL(2,R) along the lines sketched by Selberg.
and K a maximal compact subgroup
of G. The Hecke algebra
Cc(K \G/K), consisting of compactly supported K-biinvariant continuous functions on G, acts by convolution on the Hilbert space
H=L2(G / K). Because G / K is a symmetric space
, this *-algebra is commutative. The closure of its image in the operator norm is a non-unital commutative C* algebra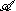
, so by the Gelfand isomorphism can be identified with the continuous functions vanishing at infinity on its spectrum
X. Points in the spectrum are given by continuous *-homomorphisms of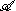
into C, i.e. characters of 
.
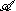If S denotes the commutant of a set of operators S on H, then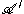
can be identified with the commutant of the regular representation
of G on H. Now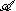
leaves invariant the subspace H0 of K-invariant vectors in H. Moreover the abelian von Neumann algebra
it generates on H0 is maximal Abelian. By spectral theory
, there is an essentially unique measure
μ on the locally compact space X and a unitary transformation U between H0 and L2(X, μ) which carries the operators in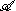
onto the corresponding multiplication operator
s.
The transformation U is called the spherical Fourier transform or sometimes just the spherical transform and μ is called the Plancherel measure
. The Hilbert space H0 can be identified with L2(K\G/K), the space of K-biinvariant square integrable functions on G.
The characters χλ of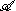
(i.e. the points of X) can be described by positive definite
spherical functions
φλ on G, via the formula
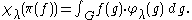
for f in Cc(K\G/K), where π(f) denotes the convolution operator in
and the integral is with respect to Haar measure
on G.
The spherical functions φλ on G are given by Harish-Chandra's formula:
In this formula:
It follows that
by the character of B = MAN given by the composition of the homomorphism of MAN onto A and the character λ.
The induced representation is defined on functions f on G with
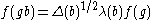
for b in B by
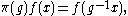
where
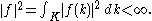
The functions f can be identified with functions in L2(K / M) and
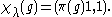
As proved, the representations of the spherical principal series are irreducible and two representations πλ and
πμ are unitarily equivalent if and only if μ = σ(λ) for some σ in the Weyl group of A.
ic upper half space
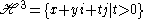
by Möbius transformations. The complex matrix
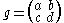
acts as
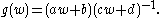
The stabiliser of the point j is the maximal compact subgroup K = SU(2), so that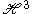
= G / K.
It carries the G-invariant Riemannian metric
with associated volume element
and Laplacian operator
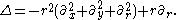
Every point in
can be written as k(etj) with k in SU(2) and t determined up to a sign.
The Laplacian has the following form on functions invariant under SU(2), regarded as functions of the real parameter t:
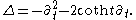
The integral of an SU(2)-invariant function is given by
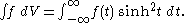
Identifying the square integrable SU(2)-invariant functions with L2(R) by the unitary transformation Uf(t) = f(t) sinh t, Δ is transformed into the operator
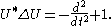
By the Plancherel theorem
and Fourier inversion formula for R, any SU(2)-invariant function f can be expressed in terms of the spherical functions
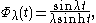
by the spherical transform
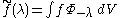
and the spherical inversion formula
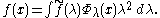
Taking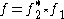
with fi in Cc(G / K) and 
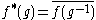, and evaluating at i yields the Plancherel formula
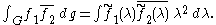
For biinvariant functions this establishes the Plancherel theorem for spherical functions: the map
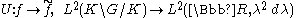
is unitary and sends the convolution operator defined by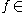
L1(K \ G / K) into the multiplication operator defined by 
.
The spherical function Φλ is an eigenfunction
of the Laplacian:
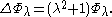
Schwartz functions on R are the spherical transforms of functions f belonging to the Harish-Chandra Schwartz space
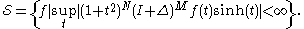
By the Paley-Wiener theorem, the spherical transforms of smooth SU(2)-invariant functions of compact support are precisely
functions on R which are restrictions of holomorphic function
s on C satisfying an exponential growth condition
As a function on G, Φλ is the matrix coefficient of the spherical principal series defined on L2(C), where C is identified with the boundary of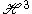
. The representation is given by the formula
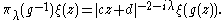
The function
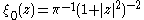
is fixed by SU(2) and
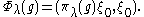
The representations πλ are irreducible and unitarily equivalent only when the sign of λ is changed.
The map W of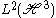
onto L2([0,∞) xC) (with measure λ2 dλ on the first factor) given by
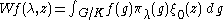
is unitary and gives the decomposition of
as a direct integral
of the spherical principal series.
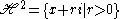
by Möbius transformations. The complex matrix
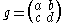
acts as
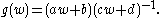
The stabiliser of the point i is the maximal compact subgroup K = SO(2), so that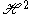
= G / K.
It carries the G-invariant Riemannian metric
with associated area element
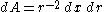
and Laplacian operator
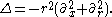
Every point in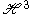
can be written as k( et i ) with k in SO(2) and t determined up to a sign. The Laplacian has the following form on functions invariant under SO(2), regarded as functions of the real parameter t:
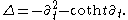
The integral of an SO(2)-invariant function is given by
There are several methods for deriving the corresponding eigenfunction expansion for this ordinary differential equation including:
The second and third technique will be described below, with two different methods of descent: the classical one due Hadamard, familiar from treatments of the heat equation and the wave equation on hyperbolic space; and Flensted-Jensen's method on the hyperboloid.
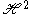and
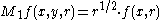
then
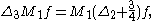
where Δn is the Laplacian on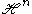
.
Since the action of SL(2,C) commutes with Δ3, the operator
M0 on S0(2)-invariant functions obtained by averaging M1f by the action of SU(2)
also satisfies
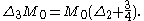
The adjoint operator M1* defined by
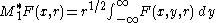
satisfies
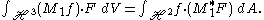
The adjoint M0*, defined by averaging M*f over SO(2), satisfies
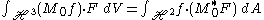
for SU(2)-invariant functions F and SO(2)-invariant functions f. It follows that
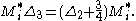
The function
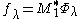
is SO(2)-invariant and satisfies
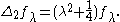
On the other hand
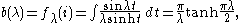
since the integral can be computed by integrating
around the rectangular
indented contour with vertices at ±R and ±R + πi. Thus the eigenfunction
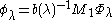
satisfies the normalisation condition φλ(i) = 1. There can only be
one such solution either because the Wronskian
of the ordinary differential equation
must vanish or by expanding as a power series in sinh r.
It follows that
Similarly it follows that
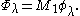
If the spherical transform of an SO(2)-invariant function on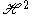
is defined by
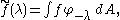
then
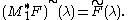
Taking f=M1*F, the SL(2,C) inversion formula for F immediately yields
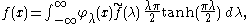
the spherical inversion formula for SO(2)-invariant functions on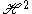
.
As for SL(2,C), this immediately implies the Plancherel formula for fi in Cc(SL(2,R) / SO(2)):
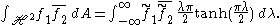
The spherical function φλ is an eigenfunction
of the Laplacian:
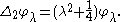
Schwartz functions on R are the spherical transforms of functions f belonging to the Harish-Chandra Schwartz space
The spherical transforms of smooth SO(2)-invariant functions of compact support are precisely
functions on R which are restrictions of holomorphic function
s on C satisfying an exponential growth condition
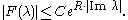
Both these results can be deduced by descent from the corresponding results for SL(2,C),
by verifying directly that the spherical transform satisfies the given growth conditions and then using the relation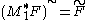
.
As a function on G, φλ is the matrix coefficient of the spherical principal series defined on L2(R), where R is identified with the boundary of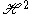
. The representation is given by the formula
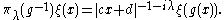
The function
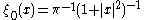
is fixed by S0(2) and
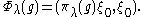
The representations πλ are irreducible and unitarily equivalent only when the sign of λ is changed.
The map W of
onto L2([0,∞) xR), with measure
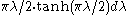
on the first factor, is given by the formula
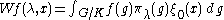
is unitary and gives the decomposition of
as a direct integral
of the spherical principal series.
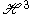. Flensted–Jensen's method uses the centraliser of SO(2) in SL(2,C) which splits as a direct product of SO(2)
and the 1-parameter subgroup K1 of matrices
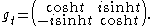
The symmetric space SL(2,C)/SU(2) can be identified with the space H3 of positive 2×2 matrices A with determinant 1
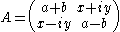
with the group action given by
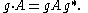
Thus
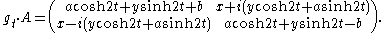
So on the hyperboloid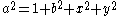
, gt only changes the coordinates y and a. Similarly the action of SO(2) acts by rotation on the coordinates (b,x) leaving a and y unchanged. The space H2 of real-valued positive matrices A with y = 0 can be identified with the orbit of the identity matrix under SL(2,R). Taking coordinates (b,x,y) in H3 and (b,x) on H2 the volume and area elements are given by
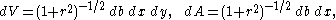
where r2 equals b2 + x2 + y2 or b2 + x2,
so that r is related to hyperbolic distance from the origin by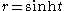
.
The Laplacian operators are given by the formula
where
and
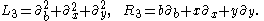
For an SU(2)-invariant function F on H3 and an SO(2)-invariant function on H2, regarded as
functions of r or t,
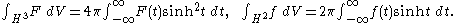
If f(b,x) is a function on H2, Ef is defined by
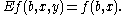
Thus
If f is SO(2)-invariant, then, regarding f as a function of r or t,
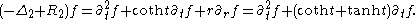
On the other hand
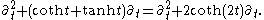
Thus, setting Sf(t) = f(2t),
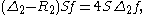
leading to the fundamental descent relation of Flensted-Jensen for M0 = ES:
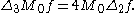
The same relation holds with M0 by M, where Mf is obtained by averaging M0f over SU(2).
The extension Ef is constant in the y variable and therefore invariant under the transformations gs. On the other hand for
F a suitable function on H3, the function QF defined by
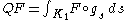
is independent of the y variable. A straightforward change of variables shows that
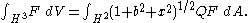
Since K1 commutes with SO(2), QF is SO(2)--invariant if F is, in particular if F is SU(2)-invariant. In this case QF is a function of r or t, so that M*F can be defined by
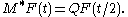
The integral formula above then yields
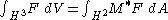
and hence, since for f SO(2)-invariant,
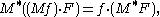
the following adjoint formula:
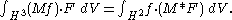
As a consequence
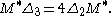
Thus, as in the case of Hadamard's method of descent.
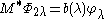
with
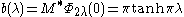
and
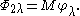
It follows that
Taking f=M*F, the SL(2,C) inversion formula for F then immediately yields
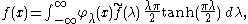
so that
Thus
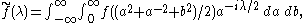
so that defining F by
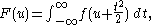
the spherical transform can be written
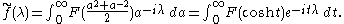
The relation between F and f is classically inverted by the Abel integral equation:
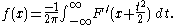
In fact
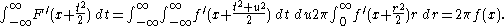
The relation between F and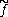
is inverted by the Fourier inversion formula:
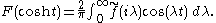
Hence
This gives the spherical inversion for the point i. Now for fixed g in SL(2,R) define
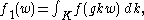
another rotation invariant function on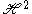
with f1(i)=f(g(i)). On the other hand for biinvariant functions f,
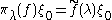
so that
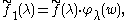
where w = g(i). Combining this with the above inversion formula for f1 yields the general spherical inversion formula:
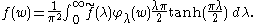
s SO0(N,1) with N odd can be treated directly by reduction to the usual Fourier transform. The remaining real Lorentz groups can be deduced by Flensted-Jensen's method of descent, as can other semisimple Lie groups of real rank one. Flensted-Jensen's method of descent also applies to the treatment of real semisimple Lie groups for which the Lie algebras are normal real forms of complex semisimple Lie algebras. The special case of SL(N,R) is treated in detail in ; this group is also the normal real form of SL(N,C).
The approach of applies to a wide class of real semisimple Lie groups of arbitrary real rank and yields the explicit product form of the Plancherel measure on
* without using Harish-Chandra's expansion of the spherical functions φλ
in terms of his c-function, discussed below. Although less general, it gives a simpler approach to the Plancherel theorem for this class of groups.
of its maximal compact subgroup U, a compact semisimple Lie group. If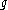
and 
are their Lie algebras, then
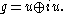
Let T be a maximal torus
in U with Lie algebra
. Then setting
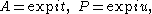
there is the Cartan decomposition
:
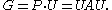
The finite-dimensional irreducible representations πλ of U are indexed by certain λ in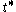
. The corresponding character formula and dimension formula of Hermann Weyl
give explicit formulas for
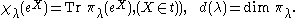
These formulas, initially defined on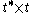
and 
, extend holomorphic to their
complexifications. Moreover
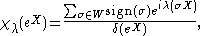
where W is the Weyl group
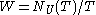and δ(eX) is given by a product formula (Weyl's denominator formula) which extends holomorphically to the complexification of
. There is a similar product formula for d(λ), a polynomial in λ.
On the complex group G, the integral of a U-biinvariant function F can be evaluated as
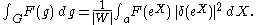
where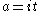
.
The spherical functions of G are labelled by λ in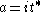
and given by the Harish-Chandra-Berezin formula
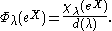
They are the matrix coefficients of the irreducible spherical principal series of G induced from the character of the Borel subgroup
of G corresponding to λ; these representations are irreducible and can all be realized on L2(U / T).
The spherical transform of a U-biinvariant function F is given by
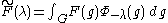
and the spherical inversion formula by
where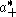
is a Weyl chamber. In fact the result follows from the Fourier inversion formula on 
since
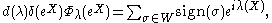
so that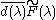
is just the Fourier transform
of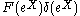
.
Note that the symmetric space
G / U has as compact dual the compact symmetric space U x U / U, where U is the diagonal subgroup. The spherical functions for the latter space, which can be identified with U itself, are the
normalized characters χλ/d(λ) indexed by lattice points in the interior of
and the role of A is played by T. The spherical transform of f of a class function
on U is given by
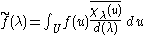
and the spherical inversion formula now follows from the theory of Fourier series
on T:
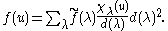
There is an evident duality between these formulas and those for the non-compact dual.
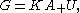
where A+ is the image of the closure of a Weyl chamber in
under the exponential map.
Moreover
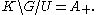
Since
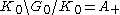
it follows that there is a canonical identification between K \ G / U, K0 \ G0 /K0 and A+. Thus K0-biinvariant functions on G0 can be identified with functions on A+ as can
functions on G that are left invariant under K and right invariant under U. Let f be a function in
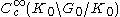and define Mf in
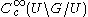by
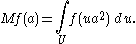
Here a third Cartan decomposition of G = UAU has been used to identify U \ G / U with A+.
Let Δ be the Laplacian on G0/K0 and let Δc be the Laplacian on G/U. Then
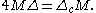
For F in
, define M*F in 
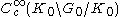by
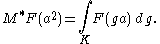
Then M and M* satisfy the duality relations
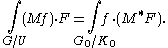
In particular
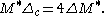
There is a similar compatibility for other operators in the center of the universal enveloping algebra
of G0. It follows from
the eigenfunction characterisation of spherical functions that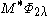
is proportional to φλ on G0, the constant of proportionality being given by
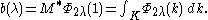
Moreover in this case
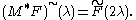
If f = M*F, then the spherical inversion formula for F on G implies that for f on G0:
since
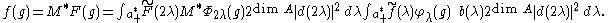
The direct calculation of the integral for b(λ), generalising the computation of for SL(2,R), was left as an open problem by . An explicit product formula for b(λ) was known from the prior determination of the Plancherel measure by
, giving
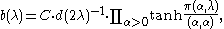
where α ranges over the positive roots of the root system
in
and C is a normalising constant, given as a quotient of products of Gamma function
s.
denote its Lie algebra. Let K be a maximal compact subgroup
given as the subgroup of fixed points of a Cartan involution σ. Let
be the ±1 eigenspaces of σ in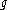 
, so that 
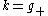is the Lie algebra of K and 
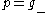give the Cartan decomposition
Let
be a maximal Abelian subalgebra of 
and for α in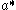 
let
If α ≠ 0 and
, then α is called a restricted root and
mα = dim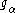
is called its multiplicity. Let A = exp 
, so
that G = KAK.The restriction of the Killing form
defines an inner product on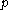
and hence 
, which allows 
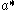to be identified with 
. With respect to this inner product, the restricted roots Σ give a root system
. Its Weyl group
can be identified with
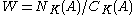. A choice of positive roots defines a Weyl chamber 
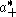. The reduced root system Σ0 consists of roots α such that α/2 is not a root.
Defining the spherical functions φ λ as above for λ in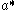
, the spherical transform of f in Cc∞(K \ G / K) is defined by
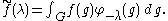
The spherical inversion formula states that
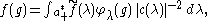
where Harish-Chandra's c-function c(λ) is defined by
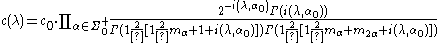
with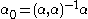
and the constant c0 chosen so that c(–iρ) = 1 where
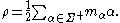
The Plancherel theorem for spherical functions states that the map
is unitary and transforms convolution by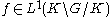
into
multiplication by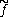
.
, that are invariant under the Weyl group W. In particular since the Laplacian Δ on G/K commutes with the action of G, it defines an second order differential operator L on 
, invariant under W, called the radial part of the Laplacian. In general
if X is in
, it defines a first order differential operator (or vector field) by
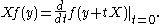
L can be expressed in terms of these operators by the formula
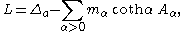
where Aα in
is defined by
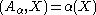
and
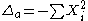
is the Laplacian on
, corresponding to any choice of orthonormal basis (Xi).
Thus
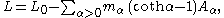
where
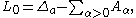
so that L can be regarded as a perturbation of the constant-coefficient operator L0.
Now the spherical function φλ is an eigenfunction of the Laplacian:
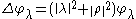
and therefore of L, when viewed as a W-invariant function on
.
Since eiλ–ρ and its transforms under W are eigenfunctions of L0 with the same eigenvalue,
it is natural look for a formula for φλ in terms of a perturbation series
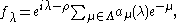
with Λ the cone of all non-negative integer combinations of positive roots, and the transforms of fλ under W. The expansion
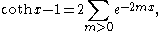
leads to a recursive formula for the coefficients aμ(λ). In particular they are uniquely determined and the
series and its derivatives converges absolutely on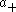
, a fundamental domain
for W. Remarkably
it turns out that fλ is also an eigenfunction of the other G-invariant differential operators on G/K, each of
which induces a W-invariant differential operator on
.
It follows that φλ can be expressed in terms as a linear combination of fλ and its transforms under W:
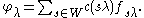
Here c(λ) is Harish-Chandra's c-function. It describes the asymptotic behaviour of φλ in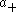
,
since
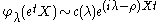
for X in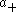
and t>0 large.
Harish-Chandra obtained a second integral formula for φλ and hence c(λ) using the Bruhat decomposition
of G:
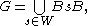
where B = MAN and the union is disjoint. Taking the Coxeter element s0 of W, the unique element mapping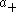
onto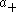 
, it follows that σ(N) has a dense open orbit G/B=K/M
whose complement is a union of cells of strictly smaller dimension and therefore has measure zero. It follows that the integral formula
for φλ initially defined over K/M
can be transferred to σ(N):
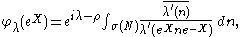
for X in
.
Since
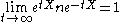
for X in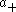
, the asymptotic behaviour of φλ can be read off from this integral, leading to the formula:
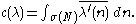
These operators all act on the same space L2(K/M), which can be identified with the representation induced from
the 1-dimensional representation defined by λ on MAN. Once A has been chosen, the compact subgroup M is uniquely determined as the centraliser of A in K. The nilpotent subgroup N, however, depends on a choice of a Weyl chamber in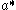
, the various choices being permuted by the Weyl group W = M ' / M, where M ' is the normaliser of A in K. The standard intertwining operator corresponding to (s, λ) is defined on the induced representation by
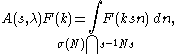
where σ is the Cartan involution. It satisfies the intertwining relation
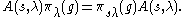
The key property of the intertwining operators and their integrals is the multiplicative cocycle property
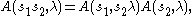
whenever
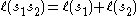
for the length function on the Weyl group associated with the choice of Weyl chamber. For s in W, this is the number of chambers
crossed by the straight line segment between X and sX for any point X in the interior of the chamber. The unique element of greatest length
s0, namely the number of positive restricted roots, is the unique element that carries the Weyl chamber
onto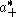 
. By Harish-Chandra's integral formula, it corresponds to Harish-Chandra's c-function:
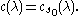
The c-functions are in general defined by the equation
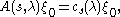
where ξ0 is the constant function 1 in L2(K/M). The cocycle property of the intertwining operators implies a similar multiplicative property for the c-functions:
provided
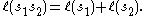
This reduces the computation of cs to the case when s = sα, the reflection in a (simple) root α, the so-called
"rank-one reduction" of . In fact the integral involves only the closed connected subgroup Gα corresponding to the Lie subalgebra generated by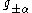
where α lies in Σ0+. Then Gα is a real semisimple Lie group with real rank one, i.e. dim Aα = 1,
and cs is just the Harish-Chandra c-function of Gα. In this case the c-function can be computed directly by various means:
This yields the following formula:
where
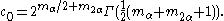
The general Gindikin–Karpelevich formula for c(λ) is an immediate consequence of this formula and the multiplicative properties of cs(λ).
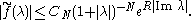
In this case f is supported in the closed ball of radius R about the origin in G/K.
This was proved by Helgason and Gangolli ( pg. 37).
The theorem was later proved by independently of the spherical inversion theorem, using a modification of his method of reduction to the complex case.
considerably simplified previous proofs.
The first step of his proof consists in showing directly that the inverse transform, defined using Harish-Chandra's c-function, defines a function supported in the closed ball of radius R about the origin if the Paley-Wiener estimate is satisfied. This follows
because the integrand defining the inverse transform extends to a meromorphic function on the complexification
of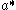
; the integral can be shifted to 
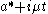for μ in 
and t > 0. Using Harish-Chandra's expansion
of φλ and the formulas for c(λ) in terms of Gamma function
s, the integral can be bounded for t large and hence can be shown to vanish outside the closed ball of radius R about the origin.
This part of the Paley-Wiener theorem shows that
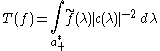
defines a distribution on G/K with support at the origin o. A further estimate for the integral shows that it is in fact given by a measure and that therefore there is a constant C such that
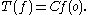
By applying this result to
it follows that
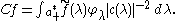
A further scaling argument allows the inequality C = 1 to be deduced from the Plancherel theorem and Paley-Wiener theorem on
.
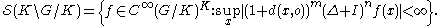
Under the spherical transform it is mapped onto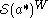
, the space of W-invariant
Schwartz functions on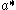
.
The original proof of Harish-Chandra was a long argument by induction. found a short and simple proof, allowing the result to be deduced directly from versions of the Paley-Wiener and spherical inversion formula. He proved that the spherical transform of a Harish-Chandra Schwartz function is a classical Schwartz function. His key observation was then to show that the inverse transform was continuous on the Paley-Wiener space endowed with classical Schwartz space seminorms, using classical estimates.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Plancherel theorem for spherical functions is an important result in the representation theory
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
of semisimple Lie groups, due in its final form to Harish-Chandra
Harish-Chandra
Harish-Chandra was an Indian mathematician, who did fundamental work in representation theory, especially Harmonic analysis on semisimple Lie groups. -Life:...
. It is a natural generalisation in non-commutative harmonic analysis of the Plancherel formula and Fourier inversion formula in the representation theory of the group of real numbers in classical harmonic analysis
Harmonic analysis
Harmonic analysis is the branch of mathematics that studies the representation of functions or signals as the superposition of basic waves. It investigates and generalizes the notions of Fourier series and Fourier transforms...
and has a similarly close interconnection with the theory of differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s.
It is the special case for zonal spherical function
Zonal spherical function
In mathematics, a zonal spherical function or often just spherical function is a function on a locally compact group G with compact subgroup K that arises as the matrix coefficient of a K-invariant vector in an irreducible representation of G...
s of the general Plancherel theorem
Plancherel theorem
In mathematics, the Plancherel theorem is a result in harmonic analysis, proved by Michel Plancherel in 1910. It states that the integral of a function's squared modulus is equal to the integral of the squared modulus of its frequency spectrum....
for semisimple Lie groups, also proved by Harish-Chandra. The Plancherel theorem gives the eigenfunction expansion
Spectral theory
In mathematics, spectral theory is an inclusive term for theories extending the eigenvector and eigenvalue theory of a single square matrix to a much broader theory of the structure of operators in a variety of mathematical spaces. It is a result of studies of linear algebra and the solutions of...
of radial functions for the Laplacian operator on the associated symmetric space
Symmetric space
A symmetric space is, in differential geometry and representation theory, a smooth manifold whose group of symmetries contains an "inversion symmetry" about every point...
X; it also gives the direct integral decomposition
Direct integral
In mathematics and functional analysis a direct integral is a generalization of the concept of direct sum. The theory is most developed for direct integrals of Hilbert spaces and direct integrals of von Neumann algebras. The concept was introduced in 1949 by John von Neumann in one of the papers...
into irreducible representations of the regular representation
Regular representation
In mathematics, and in particular the theory of group representations, the regular representation of a group G is the linear representation afforded by the group action of G on itself by translation....
on L2(X). In the case of
hyperbolic space
Hyperbolic space
In mathematics, hyperbolic space is a type of non-Euclidean geometry. Whereas spherical geometry has a constant positive curvature, hyperbolic geometry has a negative curvature: every point in hyperbolic space is a saddle point...
, these expansions were known from prior results of Mehler, Weyl and Fock
Vladimir Fock
Vladimir Aleksandrovich Fock was a Soviet physicist, who did foundational work on quantum mechanics and quantum electrodynamics....
.
The main reference for almost all this material is the encyclopedic text of .
History
The first versions of an abstract Plancherel formula for the Fourier transform on a unimodularUnimodular
In mathematics, unimodular may refer to any of the following:* unimodular lattice* unimodular matrix* unimodular polynomial matrix* unimodular form* unimodular group...
locally compact group
Locally compact group
In mathematics, a locally compact group is a topological group G which is locally compact as a topological space. Locally compact groups are important because they have a natural measure called the Haar measure. This allows one to define integrals of functions on G.Many of the results of finite...
G were due to Segal and Mautner. At around the same time, Harish-Chandra and Gelfand & Naimark derived an explicit formula for SL(2,R) and complex semisimple Lie groups, so in particular the Lorentz group
Lorentz group
In physics , the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical setting for all physical phenomena...
s. A simpler abstract formula was derived by Mautner for a "topological" symmetric space G/K corresponding to a maximal compact subgroup
Maximal compact subgroup
In mathematics, a maximal compact subgroup K of a topological group G is a subgroup K that is a compact space, in the subspace topology, and maximal amongst such subgroups....
K. Godement
Roger Godement
Roger Godement is a French mathematician, known for his work in functional analysis, and also his expository books.He started as a student at the École normale supérieure in 1940, where he became a student of Henri Cartan...
gave a more concrete and satisfactory form for positive definite
Positive definite function on a group
In operator theory, a positive-definite function on a group relates the notions of positivity, in the context of Hilbert spaces, and algebraic groups...
spherical functions
Zonal spherical function
In mathematics, a zonal spherical function or often just spherical function is a function on a locally compact group G with compact subgroup K that arises as the matrix coefficient of a K-invariant vector in an irreducible representation of G...
, a class of special functions on G/K. Since when G is a semisimple Lie group these spherical functions φλ were naturally labelled by a parameter λ in the quotient of a Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
by the action of a finite reflection group, it became a central problem to determine explicitly the Plancherel measure
Plancherel measure
In mathematics, Plancherel measure is a probability measure defined on the set of irreducible representations of a finite group G. In some cases the term Plancherel measure is applied specifically in the context of the group G being the finite symmetric group S_n – see below...
in terms of this parametrization. Generalizing the ideas of Hermann Weyl
Hermann Weyl
Hermann Klaus Hugo Weyl was a German mathematician and theoretical physicist. Although much of his working life was spent in Zürich, Switzerland and then Princeton, he is associated with the University of Göttingen tradition of mathematics, represented by David Hilbert and Hermann Minkowski.His...
from the spectral theory of ordinary differential equations
Spectral theory of ordinary differential equations
In mathematics, the spectral theory of ordinary differential equations is the part of spectral theory concerned with the determination of the spectrum and eigenfunction expansion associated with a linear ordinary differential equation...
, Harish-Chandra introduced his celebrated c-function c(λ) to describe the asymptotic behaviour of the spherical functions φλ and proposed c(λ)−2 dλ as the Plancherel measure. He verified this formula for the special cases when G is complex or real rank
Iwasawa decomposition
In mathematics, the Iwasawa decomposition KAN of a semisimple Lie group generalises the way a square real matrix can be written as a product of an orthogonal matrix and an upper triangular matrix...
one, thus in particular covering the case when G/K is a hyperbolic space
Hyperbolic space
In mathematics, hyperbolic space is a type of non-Euclidean geometry. Whereas spherical geometry has a constant positive curvature, hyperbolic geometry has a negative curvature: every point in hyperbolic space is a saddle point...
. The general case was reduced to two conjectures about the properties of the c-function and the so-called spherical Fourier transform. Explicit formulas for the c-function were later obtained for a large class of classical semisimple Lie groups by Bhanu-Murthy. In turn these formulas prompted Gindikin and Karpelevič to derive a product formula for the c-function, reducing the computation to Harish-Chandra's formula for the rank 1 case. Their work finally enabled Harish-Chandra to complete his proof of the Plancherel theorem for spherical functions in 1966.
In many special cases, for example for complex semisimple group or the Lorentz groups, there are simple methods to develop the theory directly. Certain subgroups of these groups can be treated by techniques generalising the well-known "method of descent" due to Jacques Hadamard
Jacques Hadamard
Jacques Salomon Hadamard FRS was a French mathematician who made major contributions in number theory, complex function theory, differential geometry and partial differential equations.-Biography:...
. In particular gave a general method for deducing properties of the spherical transform for a real semisimple group from that of its complexification.
One of the principal applications and motivations for the spherical transform was Selberg's trace formula. The classical Poisson summation formula
Poisson summation formula
In mathematics, the Poisson summation formula is an equation that relates the Fourier series coefficients of the periodic summation of a function to values of the function's continuous Fourier transform. Consequently, the periodic summation of a function is completely defined by discrete samples...
combines the Fourier inversion formula on a vector group with summation over a cocompact lattice. In Selberg's analogue of this formula, the vector group is replaced by G/K, the Fourier transform by the spherical transform and the lattice by a cocompact (or cofinite) discrete subgroup. The original paper of implicitly invokes the spherical transform; it was who brought the transform to the fore, giving in particular an elementary treatment for SL(2,R) along the lines sketched by Selberg.
Spherical functions
Let G be a semisimple Lie groupLie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
and K a maximal compact subgroup
Maximal compact subgroup
In mathematics, a maximal compact subgroup K of a topological group G is a subgroup K that is a compact space, in the subspace topology, and maximal amongst such subgroups....
of G. The Hecke algebra
Hecke algebra
In mathematics, the Iwahori–Hecke algebra, or Hecke algebra, named for Erich Hecke and Nagayoshi Iwahori, is a one-parameter deformation of the group algebra of a Coxeter group....
Cc(K \G/K), consisting of compactly supported K-biinvariant continuous functions on G, acts by convolution on the Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
H=L2(G / K). Because G / K is a symmetric space
Symmetric space
A symmetric space is, in differential geometry and representation theory, a smooth manifold whose group of symmetries contains an "inversion symmetry" about every point...
, this *-algebra is commutative. The closure of its image in the operator norm is a non-unital commutative C* algebra
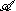, so by the Gelfand isomorphism can be identified with the continuous functions vanishing at infinity on its spectrumSpectrum
A spectrum is a condition that is not limited to a specific set of values but can vary infinitely within a continuum. The word saw its first scientific use within the field of optics to describe the rainbow of colors in visible light when separated using a prism; it has since been applied by...
X. Points in the spectrum are given by continuous *-homomorphisms of
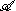into C, i.e. characters of 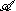.If S denotes the commutant of a set of operators S on H, then
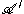can be identified with the commutant of the regular representationRegular representation
In mathematics, and in particular the theory of group representations, the regular representation of a group G is the linear representation afforded by the group action of G on itself by translation....
of G on H. Now
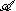leaves invariant the subspace H0 of K-invariant vectors in H. Moreover the abelian von Neumann algebraAbelian von Neumann algebra
In functional analysis, an abelian von Neumann algebra is a von Neumann algebra of operators on a Hilbert space in which all elements commute.The prototypical example of an abelian von Neumann algebra is...
it generates on H0 is maximal Abelian. By spectral theory
Spectral theory
In mathematics, spectral theory is an inclusive term for theories extending the eigenvector and eigenvalue theory of a single square matrix to a much broader theory of the structure of operators in a variety of mathematical spaces. It is a result of studies of linear algebra and the solutions of...
, there is an essentially unique measure
Measure
- Legal :* Measure of the Church of England is a law passed by the General Synod and the UK Parliament equivalent of an Act* Measure of the National Assembly for Wales, a law specific to Wales passed by the Welsh Assembly between 2007 and 2011...
μ on the locally compact space X and a unitary transformation U between H0 and L2(X, μ) which carries the operators in
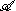onto the corresponding multiplication operatorMultiplication operator
In operator theory, a multiplication operator is a linear operator T defined on some vector space of functions and whose value at a function φ is given by multiplication by a fixed function f...
s.
The transformation U is called the spherical Fourier transform or sometimes just the spherical transform and μ is called the Plancherel measure
Plancherel measure
In mathematics, Plancherel measure is a probability measure defined on the set of irreducible representations of a finite group G. In some cases the term Plancherel measure is applied specifically in the context of the group G being the finite symmetric group S_n – see below...
. The Hilbert space H0 can be identified with L2(K\G/K), the space of K-biinvariant square integrable functions on G.
The characters χλ of
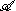(i.e. the points of X) can be described by positive definitePositive definite function on a group
In operator theory, a positive-definite function on a group relates the notions of positivity, in the context of Hilbert spaces, and algebraic groups...
spherical functions
Zonal spherical function
In mathematics, a zonal spherical function or often just spherical function is a function on a locally compact group G with compact subgroup K that arises as the matrix coefficient of a K-invariant vector in an irreducible representation of G...
φλ on G, via the formula
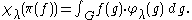
for f in Cc(K\G/K), where π(f) denotes the convolution operator in
and the integral is with respect to Haar measureHaar measure
In mathematical analysis, the Haar measure is a way to assign an "invariant volume" to subsets of locally compact topological groups and subsequently define an integral for functions on those groups....
on G.
The spherical functions φλ on G are given by Harish-Chandra's formula:
 |
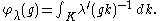In this formula:
- the integral is with respect to Haar measure on K;
- λ is an element of A* =Hom(A,T) where A is the Abelian vector subgroup in the Iwasawa decompositionIwasawa decompositionIn mathematics, the Iwasawa decomposition KAN of a semisimple Lie group generalises the way a square real matrix can be written as a product of an orthogonal matrix and an upper triangular matrix...
G =KAN of G; - λ' is defined on G by first extending λ to a characterCharacter (mathematics)In mathematics, a character is a special kind of function from a group to a field . There are at least two distinct, but overlapping meanings...
of the solvable subgroupSolvable groupIn mathematics, more specifically in the field of group theory, a solvable group is a group that can be constructed from abelian groups using extensions...
AN, using the group homomorphism onto A, and then setting
- for k in K and x in AN, where ΔAN is the modular function of AN.
- Two different characters λ1 and λ2 give the same spherical function if and only if λ1 = λ2·s, where s is in the Weyl groupWeyl groupIn mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection...
of A
- the quotient of the normaliser of A in K by its centraliser, a finite reflection group.
It follows that
- X can be identified with the quotient space A*/W.
Spherical principal series
The spherical function φλ can be identified with the matrix coefficient of the spherical principal series of G. If M is the centralizer of A in K, this is defined as the unitary representation πλ of G inducedInduced representation
In mathematics, and in particular group representation theory, the induced representation is one of the major general operations for passing from a representation of a subgroup H to a representation of the group G itself. It was initially defined as a construction by Frobenius, for linear...
by the character of B = MAN given by the composition of the homomorphism of MAN onto A and the character λ.
The induced representation is defined on functions f on G with
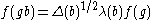
for b in B by
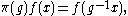
where
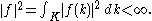
The functions f can be identified with functions in L2(K / M) and
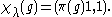
As proved, the representations of the spherical principal series are irreducible and two representations πλ and
πμ are unitarily equivalent if and only if μ = σ(λ) for some σ in the Weyl group of A.
Example: SL(2,C)
The group G = SL(2,C) acts transitively on the quaternionQuaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
ic upper half space
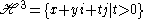
by Möbius transformations. The complex matrix
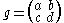
acts as
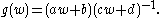
The stabiliser of the point j is the maximal compact subgroup K = SU(2), so that
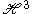= G / K.It carries the G-invariant Riemannian metric
with associated volume element
and Laplacian operator
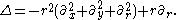
Every point in
can be written as k(etj) with k in SU(2) and t determined up to a sign.The Laplacian has the following form on functions invariant under SU(2), regarded as functions of the real parameter t:
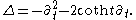
The integral of an SU(2)-invariant function is given by
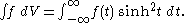
Identifying the square integrable SU(2)-invariant functions with L2(R) by the unitary transformation Uf(t) = f(t) sinh t, Δ is transformed into the operator
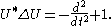
By the Plancherel theorem
Plancherel theorem
In mathematics, the Plancherel theorem is a result in harmonic analysis, proved by Michel Plancherel in 1910. It states that the integral of a function's squared modulus is equal to the integral of the squared modulus of its frequency spectrum....
and Fourier inversion formula for R, any SU(2)-invariant function f can be expressed in terms of the spherical functions
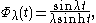
by the spherical transform
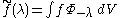
and the spherical inversion formula
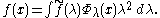
Taking
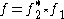with fi in Cc(G / K) and 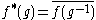, and evaluating at i yields the Plancherel formula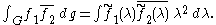For biinvariant functions this establishes the Plancherel theorem for spherical functions: the map
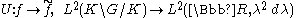
is unitary and sends the convolution operator defined by
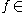L1(K \ G / K) into the multiplication operator defined by .The spherical function Φλ is an eigenfunction
Eigenfunction
In mathematics, an eigenfunction of a linear operator, A, defined on some function space is any non-zero function f in that space that returns from the operator exactly as is, except for a multiplicative scaling factor. More precisely, one has...
of the Laplacian:
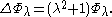
Schwartz functions on R are the spherical transforms of functions f belonging to the Harish-Chandra Schwartz space
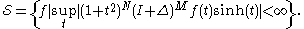
By the Paley-Wiener theorem, the spherical transforms of smooth SU(2)-invariant functions of compact support are precisely
functions on R which are restrictions of holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
s on C satisfying an exponential growth condition
As a function on G, Φλ is the matrix coefficient of the spherical principal series defined on L2(C), where C is identified with the boundary of
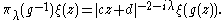
. The representation is given by the formulaThe function
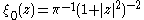
is fixed by SU(2) and
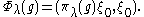
The representations πλ are irreducible and unitarily equivalent only when the sign of λ is changed.
The map W of
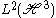onto L2([0,∞) xC) (with measure λ2 dλ on the first factor) given by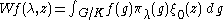is unitary and gives the decomposition of
as a direct integralDirect integral
In mathematics and functional analysis a direct integral is a generalization of the concept of direct sum. The theory is most developed for direct integrals of Hilbert spaces and direct integrals of von Neumann algebras. The concept was introduced in 1949 by John von Neumann in one of the papers...
of the spherical principal series.
Example: SL(2,R)
The group G = SL(2,R) acts transitively on the Poincaré upper half plane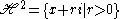by Möbius transformations. The complex matrix
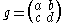
acts as
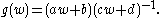
The stabiliser of the point i is the maximal compact subgroup K = SO(2), so that
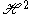= G / K.It carries the G-invariant Riemannian metric
with associated area element
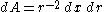
and Laplacian operator
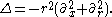
Every point in
can be written as k( et i ) with k in SO(2) and t determined up to a sign. The Laplacian has the following form on functions invariant under SO(2), regarded as functions of the real parameter t: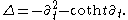The integral of an SO(2)-invariant function is given by
There are several methods for deriving the corresponding eigenfunction expansion for this ordinary differential equation including:
- the classical spectral theory of ordinary differential equationsSpectral theory of ordinary differential equationsIn mathematics, the spectral theory of ordinary differential equations is the part of spectral theory concerned with the determination of the spectrum and eigenfunction expansion associated with a linear ordinary differential equation...
applied to the hypergeometric equation (Mehler, Weyl, Fock); - variants of Hadamard's method of descent, realising 2-dimensional hyperbolic space as the quotient of 3-dimensional hyperbolic space by the free action of a 1-parameter subgroup of SL(2,C);
- Abel's integral equation, following Selberg and Godement;
- orbital integrals (Harish-Chandra, Gelfand & Naimark).
The second and third technique will be described below, with two different methods of descent: the classical one due Hadamard, familiar from treatments of the heat equation and the wave equation on hyperbolic space; and Flensted-Jensen's method on the hyperboloid.
Hadamard's method of descent
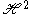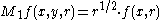
If f(x,r) is a function on andthen
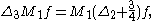
where Δn is the Laplacian on
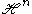.Since the action of SL(2,C) commutes with Δ3, the operator
M0 on S0(2)-invariant functions obtained by averaging M1f by the action of SU(2)
also satisfies
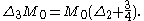
The adjoint operator M1* defined by
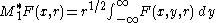
satisfies
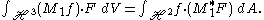
The adjoint M0*, defined by averaging M*f over SO(2), satisfies
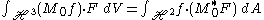
for SU(2)-invariant functions F and SO(2)-invariant functions f. It follows that
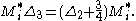
The function
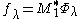
is SO(2)-invariant and satisfies
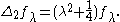
On the other hand
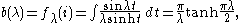
since the integral can be computed by integrating
around the rectangularindented contour with vertices at ±R and ±R + πi. Thus the eigenfunction
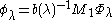
satisfies the normalisation condition φλ(i) = 1. There can only be
one such solution either because the Wronskian
Wronskian
In mathematics, the Wronskian is a determinant introduced by and named by . It is used in the study of differential equations, where it can sometimes be used to show that a set of solutions is linearly independent.-Definition:...
of the ordinary differential equation
must vanish or by expanding as a power series in sinh r.
It follows that
Similarly it follows that
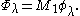
If the spherical transform of an SO(2)-invariant function on
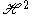is defined by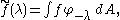then
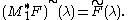
Taking f=M1*F, the SL(2,C) inversion formula for F immediately yields
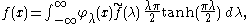
the spherical inversion formula for SO(2)-invariant functions on
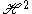.As for SL(2,C), this immediately implies the Plancherel formula for fi in Cc(SL(2,R) / SO(2)):
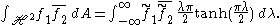
The spherical function φλ is an eigenfunction
Eigenfunction
In mathematics, an eigenfunction of a linear operator, A, defined on some function space is any non-zero function f in that space that returns from the operator exactly as is, except for a multiplicative scaling factor. More precisely, one has...
of the Laplacian:
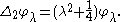
Schwartz functions on R are the spherical transforms of functions f belonging to the Harish-Chandra Schwartz space
The spherical transforms of smooth SO(2)-invariant functions of compact support are precisely
functions on R which are restrictions of holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
s on C satisfying an exponential growth condition
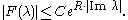
Both these results can be deduced by descent from the corresponding results for SL(2,C),
by verifying directly that the spherical transform satisfies the given growth conditions and then using the relation
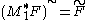.As a function on G, φλ is the matrix coefficient of the spherical principal series defined on L2(R), where R is identified with the boundary of
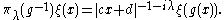
. The representation is given by the formulaThe function
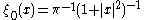
is fixed by S0(2) and
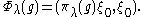
The representations πλ are irreducible and unitarily equivalent only when the sign of λ is changed.
The map W of
onto L2([0,∞) xR), with measure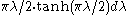on the first factor, is given by the formula
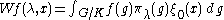
is unitary and gives the decomposition of
as a direct integralDirect integral
In mathematics and functional analysis a direct integral is a generalization of the concept of direct sum. The theory is most developed for direct integrals of Hilbert spaces and direct integrals of von Neumann algebras. The concept was introduced in 1949 by John von Neumann in one of the papers...
of the spherical principal series.
Flensted–Jensen's method of descent
Hadamard's method of descent relied on functions invariant under the action of 1-parameter subgroup of translations in the y parameter in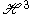. Flensted–Jensen's method uses the centraliser of SO(2) in SL(2,C) which splits as a direct product of SO(2)and the 1-parameter subgroup K1 of matrices
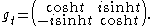
The symmetric space SL(2,C)/SU(2) can be identified with the space H3 of positive 2×2 matrices A with determinant 1
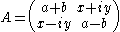
with the group action given by
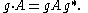
Thus
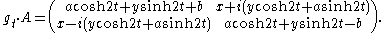
So on the hyperboloid
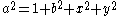, gt only changes the coordinates y and a. Similarly the action of SO(2) acts by rotation on the coordinates (b,x) leaving a and y unchanged. The space H2 of real-valued positive matrices A with y = 0 can be identified with the orbit of the identity matrix under SL(2,R). Taking coordinates (b,x,y) in H3 and (b,x) on H2 the volume and area elements are given by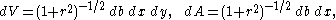where r2 equals b2 + x2 + y2 or b2 + x2,
so that r is related to hyperbolic distance from the origin by
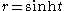.The Laplacian operators are given by the formula
where
and
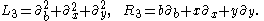
For an SU(2)-invariant function F on H3 and an SO(2)-invariant function on H2, regarded as
functions of r or t,
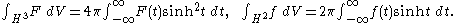
If f(b,x) is a function on H2, Ef is defined by
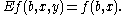
Thus
If f is SO(2)-invariant, then, regarding f as a function of r or t,
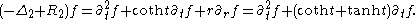
On the other hand
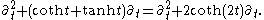
Thus, setting Sf(t) = f(2t),
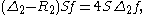
leading to the fundamental descent relation of Flensted-Jensen for M0 = ES:
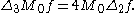
The same relation holds with M0 by M, where Mf is obtained by averaging M0f over SU(2).
The extension Ef is constant in the y variable and therefore invariant under the transformations gs. On the other hand for
F a suitable function on H3, the function QF defined by
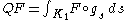
is independent of the y variable. A straightforward change of variables shows that
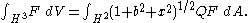
Since K1 commutes with SO(2), QF is SO(2)--invariant if F is, in particular if F is SU(2)-invariant. In this case QF is a function of r or t, so that M*F can be defined by
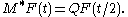
The integral formula above then yields
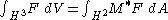
and hence, since for f SO(2)-invariant,
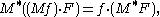
the following adjoint formula:
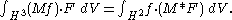
As a consequence
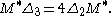
Thus, as in the case of Hadamard's method of descent.
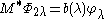
with
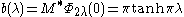
and
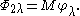
It follows that
Taking f=M*F, the SL(2,C) inversion formula for F then immediately yields
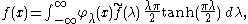
Abel's integral equation
The spherical function φλ is given byso that
Thus
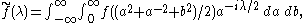
so that defining F by
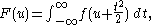
the spherical transform can be written
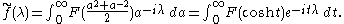
The relation between F and f is classically inverted by the Abel integral equation:
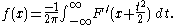
In fact
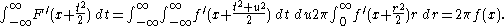
The relation between F and
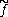is inverted by the Fourier inversion formula: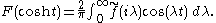Hence
This gives the spherical inversion for the point i. Now for fixed g in SL(2,R) define
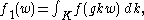
another rotation invariant function on
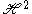with f1(i)=f(g(i)). On the other hand for biinvariant functions f,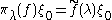so that
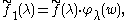
where w = g(i). Combining this with the above inversion formula for f1 yields the general spherical inversion formula:
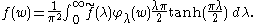
Other special cases
All complex semisimple Lie groups or the Lorentz groupLorentz group
In physics , the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical setting for all physical phenomena...
s SO0(N,1) with N odd can be treated directly by reduction to the usual Fourier transform. The remaining real Lorentz groups can be deduced by Flensted-Jensen's method of descent, as can other semisimple Lie groups of real rank one. Flensted-Jensen's method of descent also applies to the treatment of real semisimple Lie groups for which the Lie algebras are normal real forms of complex semisimple Lie algebras. The special case of SL(N,R) is treated in detail in ; this group is also the normal real form of SL(N,C).
The approach of applies to a wide class of real semisimple Lie groups of arbitrary real rank and yields the explicit product form of the Plancherel measure on
* without using Harish-Chandra's expansion of the spherical functions φλin terms of his c-function, discussed below. Although less general, it gives a simpler approach to the Plancherel theorem for this class of groups.
Complex semisimple Lie groups
If G is a complex semisimple Lie group, it is the complexificationComplexification
In mathematics, the complexification of a real vector space V is a vector space VC over the complex number field obtained by formally extending scalar multiplication to include multiplication by complex numbers. Any basis for V over the real numbers serves as a basis for VC over the complex...
of its maximal compact subgroup U, a compact semisimple Lie group. If
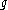and are their Lie algebras, then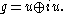Let T be a maximal torus
Maximal torus
In the mathematical theory of compact Lie groups a special role is played by torus subgroups, in particular by the maximal torus subgroups.A torus in a Lie group G is a compact, connected, abelian Lie subgroup of G . A maximal torus is one which is maximal among such subgroups...
in U with Lie algebra
. Then setting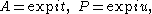there is the Cartan decomposition
Cartan decomposition
The Cartan decomposition is a decomposition of a semisimple Lie group or Lie algebra, which plays an important role in their structure theory and representation theory. It generalizes the polar decomposition of matrices.- Cartan involutions on Lie algebras :...
:
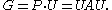
The finite-dimensional irreducible representations πλ of U are indexed by certain λ in
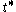. The corresponding character formula and dimension formula of Hermann WeylHermann Weyl
Hermann Klaus Hugo Weyl was a German mathematician and theoretical physicist. Although much of his working life was spent in Zürich, Switzerland and then Princeton, he is associated with the University of Göttingen tradition of mathematics, represented by David Hilbert and Hermann Minkowski.His...
give explicit formulas for
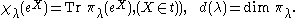
These formulas, initially defined on
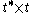and , extend holomorphic to theircomplexifications. Moreover
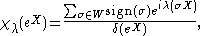
where W is the Weyl group
Weyl group
In mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection...
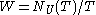and δ(eX) is given by a product formula (Weyl's denominator formula) which extends holomorphically to the complexification of. There is a similar product formula for d(λ), a polynomial in λ.On the complex group G, the integral of a U-biinvariant function F can be evaluated as
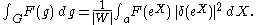
where
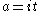.The spherical functions of G are labelled by λ in
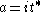and given by the Harish-Chandra-Berezin formula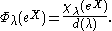They are the matrix coefficients of the irreducible spherical principal series of G induced from the character of the Borel subgroup
Borel subgroup
In the theory of algebraic groups, a Borel subgroup of an algebraic group G is a maximal Zariski closed and connected solvable algebraic subgroup.For example, in the group GLn ,...
of G corresponding to λ; these representations are irreducible and can all be realized on L2(U / T).
The spherical transform of a U-biinvariant function F is given by
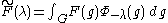
and the spherical inversion formula by
where
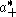is a Weyl chamber. In fact the result follows from the Fourier inversion formula on since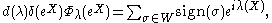so that
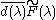is just the Fourier transformFourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
of
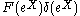.Note that the symmetric space
Symmetric space
A symmetric space is, in differential geometry and representation theory, a smooth manifold whose group of symmetries contains an "inversion symmetry" about every point...
G / U has as compact dual the compact symmetric space U x U / U, where U is the diagonal subgroup. The spherical functions for the latter space, which can be identified with U itself, are the
normalized characters χλ/d(λ) indexed by lattice points in the interior of
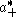and the role of A is played by T. The spherical transform of f of a class functionClass function
In mathematics, especially in the fields of group theory and representation theory of groups, a class function is a function f on a group G, such that f is constant on the conjugacy classes of G. In other words, f is invariant under the conjugation map on G...
on U is given by
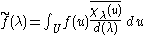
and the spherical inversion formula now follows from the theory of Fourier series
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
on T:
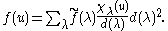
There is an evident duality between these formulas and those for the non-compact dual.
Real semisimple Lie groups
Let G0 be a normal real form of the complex semisimple Lie group G, the fixed points of an involution σ, conjugate linear on the Lie algebra of G. Let τ be a Cartan involution of G0 extended to an involution of G, complex linear on its Lie algebra, chosen to commute with σ. The fixed point subgroup of τσ is a compact real form U of G, intersecting G0 in a maximal compact subgroup K0. The fixed point subgroup of τ is K, the complexification of K0. Let G0= K0·P0 be the corresponding Cartan decomposition of G0 and let A be a maximal Abelian subgroup of P0. proved that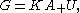where A+ is the image of the closure of a Weyl chamber in
under the exponential map.Moreover
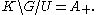
Since
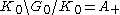
it follows that there is a canonical identification between K \ G / U, K0 \ G0 /K0 and A+. Thus K0-biinvariant functions on G0 can be identified with functions on A+ as can
functions on G that are left invariant under K and right invariant under U. Let f be a function in
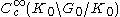and define Mf in 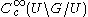by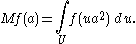Here a third Cartan decomposition of G = UAU has been used to identify U \ G / U with A+.
Let Δ be the Laplacian on G0/K0 and let Δc be the Laplacian on G/U. Then
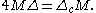
For F in
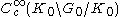, define M*F in by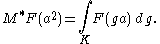Then M and M* satisfy the duality relations
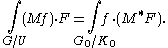
In particular
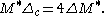
There is a similar compatibility for other operators in the center of the universal enveloping algebra
Universal enveloping algebra
In mathematics, for any Lie algebra L one can construct its universal enveloping algebra U. This construction passes from the non-associative structure L to a unital associative algebra which captures the important properties of L.Any associative algebra A over the field K becomes a Lie algebra...
of G0. It follows from
the eigenfunction characterisation of spherical functions that
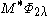is proportional to φλ on G0, the constant of proportionality being given by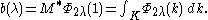Moreover in this case
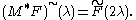
If f = M*F, then the spherical inversion formula for F on G implies that for f on G0:
since
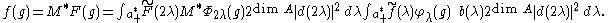
The direct calculation of the integral for b(λ), generalising the computation of for SL(2,R), was left as an open problem by . An explicit product formula for b(λ) was known from the prior determination of the Plancherel measure by
, giving
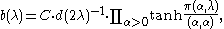
where α ranges over the positive roots of the root system
Root system
In mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras...
in
and C is a normalising constant, given as a quotient of products of Gamma functionGamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
s.
Harish-Chandra's Plancherel theorem
Let G be a noncompact connected real semisimple Lie group with finite center. Let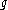 denote its Lie algebra. Let K be a maximal compact subgroupgiven as the subgroup of fixed points of a Cartan involution σ. Let
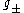be the ±1 eigenspaces of σ in 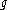, so that 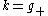is the Lie algebra of K and 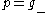give the Cartan decompositionLet
be a maximal Abelian subalgebra of and for α in 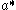letIf α ≠ 0 and
, then α is called a restricted root andmα = dim
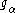is called its multiplicity. Let A = exp , sothat G = KAK.The restriction of the Killing form
Killing form
In mathematics, the Killing form, named after Wilhelm Killing, is a symmetric bilinear form that plays a basic role in the theories of Lie groups and Lie algebras...
defines an inner product on
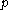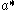and hence , which allows to be identified with . With respect to this inner product, the restricted roots Σ give a root systemRoot system
In mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras...
. Its Weyl group
Weyl group
In mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection...
can be identified with
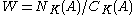. A choice of positive roots defines a Weyl chamber 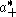. The reduced root system Σ0 consists of roots α such that α/2 is not a root.Defining the spherical functions φ λ as above for λ in
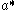, the spherical transform of f in Cc∞(K \ G / K) is defined by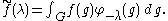The spherical inversion formula states that
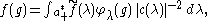
where Harish-Chandra's c-function c(λ) is defined by
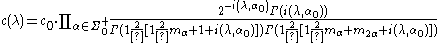
with
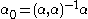and the constant c0 chosen so that c(–iρ) = 1 where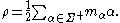The Plancherel theorem for spherical functions states that the map
is unitary and transforms convolution by
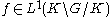intomultiplication by
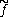.Harish-Chandra's spherical function expansion
Since G = KAK, functions on G/K that are invariant under K can be identified with functions on A, and hence, that are invariant under the Weyl group W. In particular since the Laplacian Δ on G/K commutes with the action of G, it defines an second order differential operator L on , invariant under W, called the radial part of the Laplacian. In generalif X is in
, it defines a first order differential operator (or vector field) byL can be expressed in terms of these operators by the formula
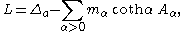
where Aα in
is defined by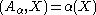and
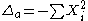
is the Laplacian on
, corresponding to any choice of orthonormal basis (Xi).Thus
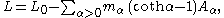
where
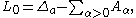
so that L can be regarded as a perturbation of the constant-coefficient operator L0.
Now the spherical function φλ is an eigenfunction of the Laplacian:
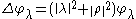
and therefore of L, when viewed as a W-invariant function on
.Since eiλ–ρ and its transforms under W are eigenfunctions of L0 with the same eigenvalue,
it is natural look for a formula for φλ in terms of a perturbation series
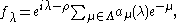
with Λ the cone of all non-negative integer combinations of positive roots, and the transforms of fλ under W. The expansion
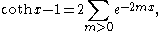
leads to a recursive formula for the coefficients aμ(λ). In particular they are uniquely determined and the
series and its derivatives converges absolutely on
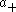, a fundamental domainFundamental domain
In geometry, the fundamental domain of a symmetry group of an object is a part or pattern, as small or irredundant as possible, which determines the whole object based on the symmetry. More rigorously, given a topological space and a group acting on it, the images of a single point under the group...
for W. Remarkably
it turns out that fλ is also an eigenfunction of the other G-invariant differential operators on G/K, each of
which induces a W-invariant differential operator on
.It follows that φλ can be expressed in terms as a linear combination of fλ and its transforms under W:
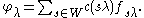
Here c(λ) is Harish-Chandra's c-function. It describes the asymptotic behaviour of φλ in
,since
for X in
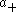and t>0 large.Harish-Chandra obtained a second integral formula for φλ and hence c(λ) using the Bruhat decomposition
Bruhat decomposition
In mathematics, the Bruhat decomposition G = BWB into cells can be regarded as a general expression of the principle of Gauss–Jordan elimination, which generically writes a matrix as a product of an upper triangular and lower triangular matrices—but with exceptional cases...
of G:
where B = MAN and the union is disjoint. Taking the Coxeter element s0 of W, the unique element mapping
onto , it follows that σ(N) has a dense open orbit G/B=K/Mwhose complement is a union of cells of strictly smaller dimension and therefore has measure zero. It follows that the integral formula
for φλ initially defined over K/M
can be transferred to σ(N):
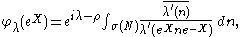
for X in
.Since
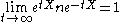
for X in
, the asymptotic behaviour of φλ can be read off from this integral, leading to the formula: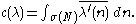Harish-Chandra's c-function
The many roles of Harish-Chandra's c-function in non-commutative harmonic analysis are surveyed in . Although it was originally introduced by Harish-Chandra in the asymptotic expansions of spherical functions, discussed above, it was also soon understood to be intimately related to intertwining operators between induced representations, first studied in this context by . These operators exhibit the unitary equivalence between πλ and πsλ for s in the Weyl group and a c-function cs(λ) can be attached to each such operator: namely the value at 1 of the intertwining operator applied to ξ0, the constant function 1, in L2(K/M). Equivalently, since ξ0 is up to scalar multiplication the unique vector fixed by K, it is an eigenvector of the intertwining operator with eigenvalue cs(λ).These operators all act on the same space L2(K/M), which can be identified with the representation induced from
the 1-dimensional representation defined by λ on MAN. Once A has been chosen, the compact subgroup M is uniquely determined as the centraliser of A in K. The nilpotent subgroup N, however, depends on a choice of a Weyl chamber in
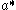, the various choices being permuted by the Weyl group W = M ' / M, where M ' is the normaliser of A in K. The standard intertwining operator corresponding to (s, λ) is defined on the induced representation by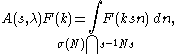where σ is the Cartan involution. It satisfies the intertwining relation
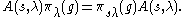
The key property of the intertwining operators and their integrals is the multiplicative cocycle property
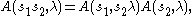
whenever
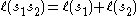
for the length function on the Weyl group associated with the choice of Weyl chamber. For s in W, this is the number of chambers
crossed by the straight line segment between X and sX for any point X in the interior of the chamber. The unique element of greatest length
s0, namely the number of positive restricted roots, is the unique element that carries the Weyl chamber
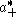onto 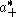. By Harish-Chandra's integral formula, it corresponds to Harish-Chandra's c-function: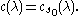The c-functions are in general defined by the equation
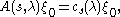
where ξ0 is the constant function 1 in L2(K/M). The cocycle property of the intertwining operators implies a similar multiplicative property for the c-functions:
provided
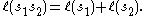
This reduces the computation of cs to the case when s = sα, the reflection in a (simple) root α, the so-called
"rank-one reduction" of . In fact the integral involves only the closed connected subgroup Gα corresponding to the Lie subalgebra generated by
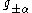where α lies in Σ0+. Then Gα is a real semisimple Lie group with real rank one, i.e. dim Aα = 1,and cs is just the Harish-Chandra c-function of Gα. In this case the c-function can be computed directly by various means:
- by noting that φλ can be expressed in terms of the hypergeometric function for which the asymptotic expansion is known from the classical formulas of Gauss for the connection coefficients;
- by directly computing the integral, which can be expressed as an integral in two variables and hence a product of two beta functions.
This yields the following formula:
where
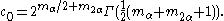
The general Gindikin–Karpelevich formula for c(λ) is an immediate consequence of this formula and the multiplicative properties of cs(λ).
Paley–Wiener theorem
The Paley-Wiener theorem generalizes the classical Paley-Wiener theorem by characterizing the spherical transforms of smooth K-bivariant functions of compact support on G. It is a necessary and sufficient condition that the spherical transform be W-invariant and that there is an R > 0 such that for each N there is an estimate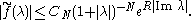In this case f is supported in the closed ball of radius R about the origin in G/K.
This was proved by Helgason and Gangolli ( pg. 37).
The theorem was later proved by independently of the spherical inversion theorem, using a modification of his method of reduction to the complex case.
Rosenberg's proof of inversion formula
noticed that the Paley-Wiener theorem and the spherical inversion theorem could be proved simultaneously, by a trick whichconsiderably simplified previous proofs.
The first step of his proof consists in showing directly that the inverse transform, defined using Harish-Chandra's c-function, defines a function supported in the closed ball of radius R about the origin if the Paley-Wiener estimate is satisfied. This follows
because the integrand defining the inverse transform extends to a meromorphic function on the complexification
Complexification
In mathematics, the complexification of a real vector space V is a vector space VC over the complex number field obtained by formally extending scalar multiplication to include multiplication by complex numbers. Any basis for V over the real numbers serves as a basis for VC over the complex...
of
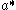; the integral can be shifted to 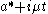for μ in and t > 0. Using Harish-Chandra's expansionof φλ and the formulas for c(λ) in terms of Gamma function
Gamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
s, the integral can be bounded for t large and hence can be shown to vanish outside the closed ball of radius R about the origin.
This part of the Paley-Wiener theorem shows that
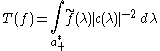
defines a distribution on G/K with support at the origin o. A further estimate for the integral shows that it is in fact given by a measure and that therefore there is a constant C such that
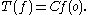
By applying this result to
it follows that
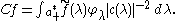
A further scaling argument allows the inequality C = 1 to be deduced from the Plancherel theorem and Paley-Wiener theorem on
.Schwartz functions
The Harish-Chandra Schwartz space can be defined as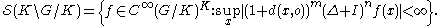Under the spherical transform it is mapped onto
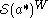, the space of W-invariantSchwartz functions on
.The original proof of Harish-Chandra was a long argument by induction. found a short and simple proof, allowing the result to be deduced directly from versions of the Paley-Wiener and spherical inversion formula. He proved that the spherical transform of a Harish-Chandra Schwartz function is a classical Schwartz function. His key observation was then to show that the inverse transform was continuous on the Paley-Wiener space endowed with classical Schwartz space seminorms, using classical estimates.