
Von Neumann algebra
Encyclopedia
In mathematics
, a von Neumann algebra or W*-algebra is a *-algebra
of bounded operators on a Hilbert space
that is closed in the weak operator topology
and contains the identity operator. They were originally introduced by John von Neumann
, motivated by his study of single operator
s, group representations, ergodic theory
and quantum mechanics
. His double commutant theorem shows that the analytic
definition is equivalent to a purely algebraic
definition as an algebra of symmetries.
Two basic examples of von Neumann algebras are as follows. The ring L∞(R) of essentially bounded measurable functions on the real line is a commutative von Neumann algebra, which acts by pointwise multiplication on the Hilbert space L2(R) of square integrable functions. The algebra B(H) of all bounded operators on a Hilbert space H is a von Neumann algebra, non-commutative if the Hilbert space has dimension at least 2.
Von Neumann algebras were first studied by ; he and Francis Murray developed the basic theory, under the original name of rings of operators, in a series of papers written in the 1930s and 1940s , reprinted in the collected works of .
Introductory accounts of von Neumann algebras are given in the online notes of and
and the books by , , and . The three volume work by gives an encyclopedic account of the theory. The book by discusses more advanced topics.
The first and most common way is to define them as weakly closed * algebras of bounded operators (on a Hilbert space) containing the identity. In this definition the weak (operator) topology can be replaced by many other common topologies
including the strong
, ultrastrong or ultraweak
operator topologies. The *-algebras of bounded operators that are closed in the norm topology are C*-algebras, so in particular any von Neumann algebra is a C*-algebra.
The second definition is that a von Neumann algebra is a subset of the bounded operators closed under * and equal to its double commutant, or equivalently the commutant of some subset closed under *. The
von Neumann double commutant theorem says that the first two definitions are equivalent.
The first two definitions describe a von Neumann algebras concretely as a set of operators acting on some given Hilbert space. showed that von Neumann algebras can also be defined abstractly as C*-algebras that have a predual
; in other words the von Neumann algebra, considered as a Banach space, is the dual of some other Banach space called the predual. The predual of a von Neumann algebra is in fact unique up to isomorphism.
Some authors use "von Neumann algebra" for the algebras together with a Hilbert space action, and "W*-algebra" for the abstract concept, so a von Neumann algebra is a W*-algebra together with a Hilbert space and a suitable faithful unital action on the Hilbert space. The concrete and abstract definitions of a von Neumann algebra are similar to the concrete and abstract definitions of a C*-algebra, which can be defined either as norm-closed * algebras of operators on a Hilbert space, or as Banach *-algebras such that ||a a*||=||a|| ||a*||.
By forgetting about the topology on a von Neumann algebra, we can consider it a (unital) *-algebra
, or just a ring. Von Neumann algebras are semihereditary: every finitely generated submodule of a projective module is itself projective. There have been several attempts to axiomatize the underlying rings of von Neumann algebras, including Baer *-rings and AW* algebras. The *-algebra of affiliated operator
s of a finite von Neumann algebra is a von Neumann regular ring
. (The von Neumann algebra itself is in general not von Neumann regular.)
s. Every commutative von Neumann algebra is isomorphic to L∞
(X) for some measure space (X, μ) and conversely, for every σ-finite measure space X, the * algebra L∞(X) is a von Neumann algebra.
Due to this analogy, the theory of von Neumann algebras has been called noncommutative measure theory, while the theory of C*-algebras is sometimes called noncommutative topology
.
A subspace of the Hilbert space H is said to belong to the von Neumann algebra M if it is the image of some projection in M. Informally these are the closed subspaces that can be described using elements of M, or that M "knows" about. The closure of the image of any operator in M, or the kernel of any operator in M belong to M, and the closure of the image of any subspace belonging to M under an operator of M also belongs to M. There is a 1:1 correspondence between projections of M and subspaces that belong to it.
The basic theory of projections was worked out by .
Two subspaces belonging to M are called (Murray-von Neumann) equivalent if there is a partial isometry mapping the first isomorphically onto the other that is an element of the von Neumann algebra (informally, if M "knows" that the subspaces are isomorphic). This induces a natural equivalence relation
on projections by defining E to be equivalent to F if the corresponding subspaces are equivalent, or in other words if there is a partial isometry
of H that maps the image of E isometrically to the image of F and is an element of the von Neumann algebra. Another way of stating this is that E is equivalent to F if E=uu* and F=u*u for some partial isometry u in M.
The equivalence relation ~ thus defined is additive in the following sense: Suppose E1 ~ F1 and E2 ~ F2. If E1 ⊥ E2 and F1 ⊥ F2, then E1 + E2 ~ F1 + F2. This is not true in general if one requires unitary equivalence in the definition of ~, i.e. if we say E is equivalent to F if u*Eu = F for some unitary u. .
The subspaces belonging to M are partially ordered by inclusion, and this induces a partial order ≤ of projections.
There is also a natural partial order on the set of equivalence classes of projections, induced by the partial order ≤ of projections. If M is a factor, ≤ is a total order on equivalence classes of projections, described in the section on traces below.
A projection (or subspace belonging to M) E is said to be finite if there is no projection F < E that is equivalent to E. For example, all finite-dimensional projections (or subspaces) are finite (since isometries between Hilbert spaces leave the dimension fixed), but the identity operator on an infinite-dimensional Hilbert space is not finite in the von Neumann algebra of all bounded operators on it, since it is isometrically isomorphic to a proper subset of itself. However it is possible for infinite dimensional subspaces to be finite.
Orthogonal projections are noncommutative analogues of indicator functions in L∞(R). L∞(R) is the ||·||∞-closure of the subspace generated by the indicator functions. Similarly, a von Neumann algebra is generated by its projections; this is a consequence of the spectral theorem for self-adjoint operators.
The projections of a finite factor form a continuous geometry
.
consists only of multiples of the identity operator is called a factor. showed that every von Neumann algebra on a separable Hilbert space is isomorphic to a direct integral
of factors. This decomposition is essentially unique. Thus, the problem of classifying isomorphism classes of von Neumann algebras on separable Hilbert spaces can be reduced to that of classifying isomorphism classes of factors.
showed that every factor has one of 3 types as described below.
The type classification can be extended to von Neumann algebras that are not factors, and a von Neumann algebra is of type X if it can be decomposed as a direct integral of type X factors; for example, every commutative von Neumann algebra has type I1. Every von Neumann algebra can be written
uniquely as a sum of von Neumann algebras of types I, II, and III.
There are several other ways to divide factors into classes that are sometimes used:
, isomorphism classes of factors of type I correspond exactly to the cardinal numbers. Since many authors consider von Neumann algebras only on separable Hilbert spaces, it is customary to call the bounded operators on a Hilbert space of finite dimension n a factor of type In, and the bounded operators on a separable infinite-dimensional Hilbert space, a factor of type I∞.
These are the unique hyperfinite factors of types II1 and II∞; there are an uncountable number of other
factors of these types that are the subject of intensive study. proved the fundamental result that
a factor of type II1 has a unique finite tracial state,
and the set of traces of projections is [0,1].
A factor of type II∞ has a semifinite trace, unique up to
rescaling, and the set of traces of projections is [0,∞]. The set of real numbers λ such that there is an automorphism rescaling the trace by a factor of λ is called the fundamental group of the type II∞ factor.
The tensor product of a factor of type II1 and an infinite
type I factor has type II∞, and conversely any factor of
type II∞ can be constructed like this. The fundamental group of a type
II1 factor is defined to be the fundamental group of its tensor product with the infinite (separable) factor of type I. For many years it was an open problem to find a type II factor whose fundamental group was not the group of all positive reals, but Connes
then showed that the von Neumann group algebra of a countable discrete group with Kazhdan's property T (the trivial representation is isolated in the dual space), such as SL3(Z), has a countable fundamental group. Subsequently Sorin Popa showed that the fundamental group can be trivial for certain groups, including the semidirect product
of Z2 by SL2(Z).
An example of a type II1 factor is the von Neumann group algebra
of a countable infinite discrete group such that every non-trivial conjugacy class is infinite.
found an uncountable family of such groups with non-isomorphic von Neumann group algebras, thus showing the existence of uncountably many different separable type II1 factors.
are equivalent. At one time type III factors were considered to be intractable objects, but Tomita–Takesaki theory
has led to a good structure theory. In particular, any type III factor can be written in a canonical way as the crossed product
of a type II∞ factor and the real numbers.
The definition of the predual given above seems to depend on the choice of Hilbert space that M acts on, as this determines the ultraweak topology.
However the predual can also be defined without using the Hilbert space that M acts on, by defining it to be the space generated by all positive normal linear functionals on M.
(Here "normal" means that it preserves suprema when applied to increasing nets of self adjoint operators; or equivalently to increasing sequences of projections.)
The predual M* is a closed subspace of the dual M* (which consists of all norm-continuous linear functionals on M) but is generally smaller. The proof that M* is (usually) not the same as M* is nonconstructive and uses the axiom of choice in an essential way; it is very hard to exhibit explicit elements of M* that are not in M*. For example, exotic positive linear forms on the von Neumann algebra l∞ (Z) are given by free ultrafilters
; they correspond to exotic *-homomorphisms into C and describe the Stone-Cech compactification of Z.
Examples:
Any factor has a trace such that the trace of a non-zero projection is non-zero
and the trace of a projection is infinite if and only if
the projection is infinite.
Such a trace is unique up to rescaling. For factors that are separable or finite, two projections are equivalent if and only if they have the same trace. The type of a factor can be read off from the possible values of this trace as follows:
If a von Neumann algebra acts on a Hilbert space containing a norm 1 vector v,
then the functional a → (av,v) is a normal state. This construction can be reversed to give an action on
a Hilbert space from a normal state: this is the GNS construction for normal states.
A module is called standard if it has a cyclic separating vector. Each factor has a standard representation, which is unique up to isomorphism. The standard representation has an antilinear involution J such that JMJ = M′.
For finite factors the standard module is given by the GNS construction applied to the unique normal tracial state and the M-dimension is normalized so that the standard module has M-dimension 1, while for infinite factors the standard module is the module with M-dimension equal to ∞.
The possible M-dimensions of modules are given as follows:
on a separable Hilbert space H are all equivalent:
There is no generally accepted term for the class of algebras above; Connes has suggested that amenable should be the standard term.
The amenable factors have been classified: there is a unique one of each of the types In, I∞, II1, II∞, IIIλ,
for 0<λ≤ 1, and the ones of type III0 correspond to certain ergodic
flows. (For type III0 calling this a classification is a little misleading, as it is known that there is no easy way to classify the corresponding ergodic flows.) The ones of type I and II1 were classified by , and the remaining ones were classified by , except for the type III1 case
which was completed by Haagerup.
All amenable factors can be constructed using the group-measure space construction
of Murray and von Neumann for a single ergodic transformation. In fact they are precisely the factors arising as crossed product
s by free ergodic actions of Z or Zn on abelian von Neumann algebras L∞(X). Type I factors occur when the measure space X is atomic
and the action transitive. When X is diffuse or non-atomic
, it is equivalent
to [0,1] as a measure space. Type II factors occur when X admits an equivalent
finite (II1) or infinite (II∞,) measure, invariant under an action of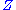 . Type III factors occur in the remaining cases where there is no invariant measure, but only an invariant measure class
. Type III factors occur in the remaining cases where there is no invariant measure, but only an invariant measure class
: these factors are called Krieger factors.
One can define a tensor product of von Neumann algebras (a completion of the algebraic tensor product of the algebras considered as rings), which is again a von Neumann algebra, and act on the tensor product of the corresponding Hilbert spaces. The tensor product of two finite algebras is finite, and the tensor product of an infinite algebra and a non-zero algebra is infinite. The type of the tensor product of two von Neumann algebras (I, II, or III) is the maximum of their types. The commutation theorem for tensor products states that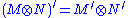
(where M′ denotes the commutant of M).
The tensor product of an infinite number of von Neumann algebras, if done naively, is usually a ridiculously large non-separable algebra. Instead showed that one should choose a state on each of the von Neumann algebras, use this to define a state on the algebraic tensor product, which can be used to product a Hilbert space and a (reasonably small) von Neumann algebra. studied the case where all the factors are finite matrix algebras; these factors are called Araki-Woods factors or ITPFI factors (ITPFI stands for "infinite tensor product of finite type I factors"). The type of the infinite tensor product can vary dramatically as the states are changed; for example, the infinite tensor product of an infinite number of type I2 factors can have any type depending on the choice of states. In particular found an uncountable family of non-isomorphic hyperfinite type IIIλ factors for 0<λ<1, called Powers factors, by taking an infinite tensor product of
type I2 factors, each with the state given by :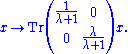
All hyperfinite von Neumann algebras not of type III0 are isomorphic to Araki-Woods factors, but there are uncountably many of type III0 that are not.
bimodule
(or correspondence) is a Hilbert space H with module actions of two commuting von Neumann algebras. Bimodules have a much richer structure than that of modules. Any bimodule over two factors always gives a subfactor
since one of the factors is always contained in the commutant of the other. There is also a subtle relative tensor product operation due to Connes
on bimodules. The theory of subfactor
s, initiated by Vaughan Jones
, reconciles these two seemingly different points of view.
Bimodules are also important for the von Neumann group algebra M of a discrete group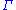 . Indeed if V is any unitary representation
. Indeed if V is any unitary representation
of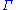 , then, regarding
, then, regarding 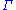 as the diagonal subgroup of
as the diagonal subgroup of 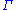 x
x 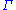 , the corresponding induced representation
, the corresponding induced representation
on l2 (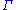 ,V) is naturally a bimodule for two commuting copies of M. Important representation theoretic
,V) is naturally a bimodule for two commuting copies of M. Important representation theoretic
properties of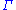 can be formulated entirely in terms of bimodules and therefore make sense for the von Neumann algebra itself. For example Connes
can be formulated entirely in terms of bimodules and therefore make sense for the von Neumann algebra itself. For example Connes
and Jones
gave a definition of an analogue of Kazhdan's Property T for von Neumann algebras in this way.
has shown that the class of non-amenable factors coming from the group-measure space construction is disjoint from the class coming from group von Neumann algebras of free groups. Later Narutaka Ozawa proved that group von Neumann algebras of hyperbolic group
s yield prime
type II1 factors, i.e. ones that cannot be factored as tensor products of type II1 factors, a result first proved by Leeming Ge for free group factors using Voiculescu's free entropy.
Popa's work on fundamental groups of non-amenable factors represents another significant advance. The theory of factors "beyond the hyperfinite" is rapidly expanding at present, with many new and surprising results; it has close links with rigidity phenomena
in geometric group theory
and ergodic theory
.
, statistical mechanics
, Quantum field theory
, Local quantum physics, Free probability
, Noncommutative geometry
, representation theory
, geometry
, and probability
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a von Neumann algebra or W*-algebra is a *-algebra
Star-algebra
-*-ring:In mathematics, a *-ring is an associative ring with a map * : A → A which is an antiautomorphism and an involution.More precisely, * is required to satisfy the following properties:* ^* = x^* + y^** ^* = y^* x^** 1^* = 1...
of bounded operators on a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
that is closed in the weak operator topology
Weak operator topology
In functional analysis, the weak operator topology, often abbreviated WOT, is the weakest topology on the set of bounded operators on a Hilbert space H, such that the functional sending an operator T to the complex number is continuous for any vectors x and y in the Hilbert space.Equivalently, a...
and contains the identity operator. They were originally introduced by John von Neumann
John von Neumann
John von Neumann was a Hungarian-American mathematician and polymath who made major contributions to a vast number of fields, including set theory, functional analysis, quantum mechanics, ergodic theory, geometry, fluid dynamics, economics and game theory, computer science, numerical analysis,...
, motivated by his study of single operator
Operator theory
In mathematics, operator theory is the branch of functional analysis that focuses on bounded linear operators, but which includes closed operators and nonlinear operators.Operator theory also includes the study of algebras of operators....
s, group representations, ergodic theory
Ergodic theory
Ergodic theory is a branch of mathematics that studies dynamical systems with an invariant measure and related problems. Its initial development was motivated by problems of statistical physics....
and quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
. His double commutant theorem shows that the analytic
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
definition is equivalent to a purely algebraic
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
definition as an algebra of symmetries.
Two basic examples of von Neumann algebras are as follows. The ring L∞(R) of essentially bounded measurable functions on the real line is a commutative von Neumann algebra, which acts by pointwise multiplication on the Hilbert space L2(R) of square integrable functions. The algebra B(H) of all bounded operators on a Hilbert space H is a von Neumann algebra, non-commutative if the Hilbert space has dimension at least 2.
Von Neumann algebras were first studied by ; he and Francis Murray developed the basic theory, under the original name of rings of operators, in a series of papers written in the 1930s and 1940s , reprinted in the collected works of .
Introductory accounts of von Neumann algebras are given in the online notes of and
and the books by , , and . The three volume work by gives an encyclopedic account of the theory. The book by discusses more advanced topics.
Definitions
There are three common ways to define von Neumann algebras.The first and most common way is to define them as weakly closed * algebras of bounded operators (on a Hilbert space) containing the identity. In this definition the weak (operator) topology can be replaced by many other common topologies
Operator topology
In the mathematical field of functional analysis there are several standard topologies which are given to the algebra B of bounded linear operators on a Hilbert space H.-Introduction:...
including the strong
Strong operator topology
In functional analysis, a branch of mathematics, the strong operator topology, often abbreviated SOT, is the weakest locally convex topology on the set of bounded operators on a Hilbert space such that the evaluation map sending an operator T to the real number \|Tx\| is continuous for each vector...
, ultrastrong or ultraweak
Ultraweak topology
In functional analysis, a branch of mathematics, the ultraweak topology, also called the weak-* topology, or weak-* operator topology or σ-weak topology, on the set B of bounded operators on a Hilbert space is the weak-* topology obtained from the predual B* of B, the trace class operators on H...
operator topologies. The *-algebras of bounded operators that are closed in the norm topology are C*-algebras, so in particular any von Neumann algebra is a C*-algebra.
The second definition is that a von Neumann algebra is a subset of the bounded operators closed under * and equal to its double commutant, or equivalently the commutant of some subset closed under *. The
von Neumann double commutant theorem says that the first two definitions are equivalent.
The first two definitions describe a von Neumann algebras concretely as a set of operators acting on some given Hilbert space. showed that von Neumann algebras can also be defined abstractly as C*-algebras that have a predual
Predual
In mathematics, the predual of an object D is an object P whose dual space is D.For example, the predual of the space of bounded operators is the space of trace class operators. The predual of the space of differential forms is the space of chainlets....
; in other words the von Neumann algebra, considered as a Banach space, is the dual of some other Banach space called the predual. The predual of a von Neumann algebra is in fact unique up to isomorphism.
Some authors use "von Neumann algebra" for the algebras together with a Hilbert space action, and "W*-algebra" for the abstract concept, so a von Neumann algebra is a W*-algebra together with a Hilbert space and a suitable faithful unital action on the Hilbert space. The concrete and abstract definitions of a von Neumann algebra are similar to the concrete and abstract definitions of a C*-algebra, which can be defined either as norm-closed * algebras of operators on a Hilbert space, or as Banach *-algebras such that ||a a*||=||a|| ||a*||.
Terminology
Some of the terminology in von Neumann algebra theory can be confusing, and the terms often have different meanings outside the subject.- A factor is a von Neumann algebra with trivial center, i.e. a center consisting only of scalar operators.
- A finite von Neumann algebra is one which is the direct integral of finite factors. Similarly, properly infinite von Neumann algebras are the direct integral of properly infinite factors.
- A von Neumann algebra that acts on a separable Hilbert space is called separable. Note that such algebras are rarely separable in the norm topology.
- The von Neumann algebra generated by a set of bounded operators on a Hilbert space is the smallest von Neumann algebra containing all those operators.
- The tensor product of two von Neumann algebras acting on two Hilbert spaces is defined to be the von Neumann algebra generated by their algebraic tensor product, considered as operators on the Hilbert space tensor product of the Hilbert spaces.
By forgetting about the topology on a von Neumann algebra, we can consider it a (unital) *-algebra
Star-algebra
-*-ring:In mathematics, a *-ring is an associative ring with a map * : A → A which is an antiautomorphism and an involution.More precisely, * is required to satisfy the following properties:* ^* = x^* + y^** ^* = y^* x^** 1^* = 1...
, or just a ring. Von Neumann algebras are semihereditary: every finitely generated submodule of a projective module is itself projective. There have been several attempts to axiomatize the underlying rings of von Neumann algebras, including Baer *-rings and AW* algebras. The *-algebra of affiliated operator
Affiliated operator
In mathematics, affiliated operators were introduced by Murray and von Neumann in the theory of von Neumann algebras as a technique for using unbounded operators to study modules generated by a single vector...
s of a finite von Neumann algebra is a von Neumann regular ring
Von Neumann regular ring
In mathematics, a von Neumann regular ring is a ring R such that for every a in R there exists an x in R withOne may think of x as a "weak inverse" of a...
. (The von Neumann algebra itself is in general not von Neumann regular.)
Commutative von Neumann algebras
The relationship between commutative von Neumann algebras and measure spaces is analogous to that between commutative C*-algebras and locally compact Hausdorff spaceHausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
s. Every commutative von Neumann algebra is isomorphic to L∞
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
(X) for some measure space (X, μ) and conversely, for every σ-finite measure space X, the * algebra L∞(X) is a von Neumann algebra.
Due to this analogy, the theory of von Neumann algebras has been called noncommutative measure theory, while the theory of C*-algebras is sometimes called noncommutative topology
Noncommutative topology
Noncommutative topology in mathematics is a term applied to the strictly C*-algebraic part of the noncommutative geometry program. The program has its origins in the Gel'fand duality between the topology of locally compact spaces and the algebraic structure of commutative C*-algebras.Several...
.
Projections
Operators E in a von Neumann algebra for which E = EE = E* are called projections; they are exactly the operators which give an orthogonal projection of H onto some closed subspace.A subspace of the Hilbert space H is said to belong to the von Neumann algebra M if it is the image of some projection in M. Informally these are the closed subspaces that can be described using elements of M, or that M "knows" about. The closure of the image of any operator in M, or the kernel of any operator in M belong to M, and the closure of the image of any subspace belonging to M under an operator of M also belongs to M. There is a 1:1 correspondence between projections of M and subspaces that belong to it.
The basic theory of projections was worked out by .
Two subspaces belonging to M are called (Murray-von Neumann) equivalent if there is a partial isometry mapping the first isomorphically onto the other that is an element of the von Neumann algebra (informally, if M "knows" that the subspaces are isomorphic). This induces a natural equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
on projections by defining E to be equivalent to F if the corresponding subspaces are equivalent, or in other words if there is a partial isometry
Partial isometry
In functional analysis a partial isometry is a linear map W between Hilbert spaces H and K such that the restriction of W to the orthogonal complement of its kernel is an isometry...
of H that maps the image of E isometrically to the image of F and is an element of the von Neumann algebra. Another way of stating this is that E is equivalent to F if E=uu* and F=u*u for some partial isometry u in M.
The equivalence relation ~ thus defined is additive in the following sense: Suppose E1 ~ F1 and E2 ~ F2. If E1 ⊥ E2 and F1 ⊥ F2, then E1 + E2 ~ F1 + F2. This is not true in general if one requires unitary equivalence in the definition of ~, i.e. if we say E is equivalent to F if u*Eu = F for some unitary u. .
The subspaces belonging to M are partially ordered by inclusion, and this induces a partial order ≤ of projections.
There is also a natural partial order on the set of equivalence classes of projections, induced by the partial order ≤ of projections. If M is a factor, ≤ is a total order on equivalence classes of projections, described in the section on traces below.
A projection (or subspace belonging to M) E is said to be finite if there is no projection F < E that is equivalent to E. For example, all finite-dimensional projections (or subspaces) are finite (since isometries between Hilbert spaces leave the dimension fixed), but the identity operator on an infinite-dimensional Hilbert space is not finite in the von Neumann algebra of all bounded operators on it, since it is isometrically isomorphic to a proper subset of itself. However it is possible for infinite dimensional subspaces to be finite.
Orthogonal projections are noncommutative analogues of indicator functions in L∞(R). L∞(R) is the ||·||∞-closure of the subspace generated by the indicator functions. Similarly, a von Neumann algebra is generated by its projections; this is a consequence of the spectral theorem for self-adjoint operators.
The projections of a finite factor form a continuous geometry
Continuous geometry
In mathematics, continuous geometry is an analogue of complex projective geometry introduced by , where instead of the dimension of a subspace being in a discrete set 0, 1, ..., n, it can be an element of the unit interval [0,1]...
.
Factors
A von Neumann algebra N whose centerCenter (algebra)
The term center or centre is used in various contexts in abstract algebra to denote the set of all those elements that commute with all other elements. It is often denoted Z, from German Zentrum, meaning "center". More specifically:...
consists only of multiples of the identity operator is called a factor. showed that every von Neumann algebra on a separable Hilbert space is isomorphic to a direct integral
Direct integral
In mathematics and functional analysis a direct integral is a generalization of the concept of direct sum. The theory is most developed for direct integrals of Hilbert spaces and direct integrals of von Neumann algebras. The concept was introduced in 1949 by John von Neumann in one of the papers...
of factors. This decomposition is essentially unique. Thus, the problem of classifying isomorphism classes of von Neumann algebras on separable Hilbert spaces can be reduced to that of classifying isomorphism classes of factors.
showed that every factor has one of 3 types as described below.
The type classification can be extended to von Neumann algebras that are not factors, and a von Neumann algebra is of type X if it can be decomposed as a direct integral of type X factors; for example, every commutative von Neumann algebra has type I1. Every von Neumann algebra can be written
uniquely as a sum of von Neumann algebras of types I, II, and III.
There are several other ways to divide factors into classes that are sometimes used:
- A factor is called discrete (or occasionally tame) if it has type I, and continuous (or occasionally wild) if it has type II or III.
- A factor is called semifinite if it has type I or II, and purely infinite if it has type III.
- A factor is called finite if the projection 1 is finite and properly infinite otherwise. Factors of types I and II may be either finite or properly infinite, but factors of type III are always properly infinite.
Type I factors
A factor is said to be of type I if there is a minimal projection E ≠ 0, i.e. a projection E such that there is no other projection F with 0 < F < E. Any factor of type I is isomorphic to the von Neumann algebra of all bounded operators on some Hilbert space; since there is one Hilbert space for every cardinal numberCardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
, isomorphism classes of factors of type I correspond exactly to the cardinal numbers. Since many authors consider von Neumann algebras only on separable Hilbert spaces, it is customary to call the bounded operators on a Hilbert space of finite dimension n a factor of type In, and the bounded operators on a separable infinite-dimensional Hilbert space, a factor of type I∞.
Type II factors
A factor is said to be of type II if there are no minimal projections but there are non-zero finite projections. This implies that every projection E can be halved in the sense that there are equivalent projections F and G such that E = F + G. If the identity operator in a type II factor is finite, the factor is said to be of type II1; otherwise, it is said to be of type II∞. The best understood factors of type II are the hyperfinite type II1 factor and the hyperfinite type II∞ factor, found by .These are the unique hyperfinite factors of types II1 and II∞; there are an uncountable number of other
factors of these types that are the subject of intensive study. proved the fundamental result that
a factor of type II1 has a unique finite tracial state,
and the set of traces of projections is [0,1].
A factor of type II∞ has a semifinite trace, unique up to
rescaling, and the set of traces of projections is [0,∞]. The set of real numbers λ such that there is an automorphism rescaling the trace by a factor of λ is called the fundamental group of the type II∞ factor.
The tensor product of a factor of type II1 and an infinite
type I factor has type II∞, and conversely any factor of
type II∞ can be constructed like this. The fundamental group of a type
II1 factor is defined to be the fundamental group of its tensor product with the infinite (separable) factor of type I. For many years it was an open problem to find a type II factor whose fundamental group was not the group of all positive reals, but Connes
Alain Connes
Alain Connes is a French mathematician, currently Professor at the Collège de France, IHÉS, The Ohio State University and Vanderbilt University.-Work:...
then showed that the von Neumann group algebra of a countable discrete group with Kazhdan's property T (the trivial representation is isolated in the dual space), such as SL3(Z), has a countable fundamental group. Subsequently Sorin Popa showed that the fundamental group can be trivial for certain groups, including the semidirect product
Semidirect product
In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
of Z2 by SL2(Z).
An example of a type II1 factor is the von Neumann group algebra
of a countable infinite discrete group such that every non-trivial conjugacy class is infinite.
found an uncountable family of such groups with non-isomorphic von Neumann group algebras, thus showing the existence of uncountably many different separable type II1 factors.
Type III factors
Lastly, type III factors are factors that do not contain any nonzero finite projections at all. In their first paper were unable to decide whether or not they existed; the first examples were later found by . Since the identity operator is always infinite in those factors, they were sometimes called type III∞ in the past, but recently that notation has been superseded by the notation IIIλ, where λ is a real number in the interval [0,1]. More precisely, if the Connes spectrum (of its modular group) is 1 then the factor is of type III0, if the Connes spectrum is all integral powers of λ for 0 < λ < 1, then the type is IIIλ, and if the Connes spectrum is all positive reals then the type is III1. (The Connes spectrum is a closed subgroup of the positive reals, so these are the only possibilities.) The only trace on type III factors takes value ∞ on all non-zero positive elements, and any two non-zero projectionsare equivalent. At one time type III factors were considered to be intractable objects, but Tomita–Takesaki theory
has led to a good structure theory. In particular, any type III factor can be written in a canonical way as the crossed product
Crossed product
In mathematics, and more specifically in the theory of von Neumann algebras, a crossed productis a basic method of constructing a new von Neumann algebra froma von Neumann algebra acted on by a group. It is related to...
of a type II∞ factor and the real numbers.
The predual
Any von Neumann algebra M has a predual M*, which is the Banach space of all ultraweakly continuous linear functionals on M. As the name suggests, M is (as a Banach space) the dual of its predual. The predual is unique in the sense that any other Banach space whose dual is M is canonically isomorphic to M*. showed that the existence of a predual characterizes von Neumann algebras among C* algebras.The definition of the predual given above seems to depend on the choice of Hilbert space that M acts on, as this determines the ultraweak topology.
However the predual can also be defined without using the Hilbert space that M acts on, by defining it to be the space generated by all positive normal linear functionals on M.
(Here "normal" means that it preserves suprema when applied to increasing nets of self adjoint operators; or equivalently to increasing sequences of projections.)
The predual M* is a closed subspace of the dual M* (which consists of all norm-continuous linear functionals on M) but is generally smaller. The proof that M* is (usually) not the same as M* is nonconstructive and uses the axiom of choice in an essential way; it is very hard to exhibit explicit elements of M* that are not in M*. For example, exotic positive linear forms on the von Neumann algebra l∞ (Z) are given by free ultrafilters
Ultrafilter
In the mathematical field of set theory, an ultrafilter on a set X is a collection of subsets of X that is a filter, that cannot be enlarged . An ultrafilter may be considered as a finitely additive measure. Then every subset of X is either considered "almost everything" or "almost nothing"...
; they correspond to exotic *-homomorphisms into C and describe the Stone-Cech compactification of Z.
Examples:
- The predual of the von Neumann algebra L∞(R) of essentially bounded functions on R is the Banach space L1(R) of integrable functions. The dual of L∞(R) is strictly larger than L1(R) For example, a functional on L∞(R) that extends the Dirac measure δ0 on the closed subspace of bounded continuous functions C0b(R) cannot be represented as a function in L1(R).
- The predual of the von Neumann algebra B(H) of bounded operators on a Hilbert space H is the Banach space of all trace classTrace classIn mathematics, a trace class operator is a compact operator for which a trace may be defined, such that the trace is finite and independent of the choice of basis....
operators with the trace norm ||A||= Tr(|A|). The Banach space of trace class operators is itself the dual of the C*-algebra of compact operators (which is not a von Neumann algebra).
Weights, states, and traces
Weights and their special cases states and traces are discussed in detail in .- A weight ω on a von Neumann algebra is a linear map from the set of positive elements (those of the form a*a) to [0,∞].
- A positive linear functional is a weight with ω(1) finite (or rather the extension of ω to the whole algebra by linearity).
- A stateState (functional analysis)In functional analysis, a state on a C*-algebra is a positive linear functional of norm 1. The set of states of a C*-algebra A, sometimes denoted by S, is always a convex set. The extremal points of S are called pure states...
is a weight with ω(1)=1.
- A trace is a weight with ω(aa*)=ω(a*a) for all a.
- A tracial state is a trace with ω(1)=1.
Any factor has a trace such that the trace of a non-zero projection is non-zero
and the trace of a projection is infinite if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
the projection is infinite.
Such a trace is unique up to rescaling. For factors that are separable or finite, two projections are equivalent if and only if they have the same trace. The type of a factor can be read off from the possible values of this trace as follows:
- Type In: 0, x, 2x, ....,nx for some positive x (usually normalized to be 1/n or 1).
- Type I∞: 0, x, 2x, ....,∞ for some positive x (usually normalized to be 1).
- Type II1: [0,x] for some positive x (usually normalized to be 1).
- Type II∞: [0,∞].
- Type III: 0,∞.
If a von Neumann algebra acts on a Hilbert space containing a norm 1 vector v,
then the functional a → (av,v) is a normal state. This construction can be reversed to give an action on
a Hilbert space from a normal state: this is the GNS construction for normal states.
Modules over a factor
Given an abstract separable factor, one can ask for a classification of its modules, meaning the separable Hilbert spaces that it acts on. The answer is given as follows: every such module H can be given an M-dimension dimM(H) (not its dimension as a complex vector space) such that modules are isomorphic if and only if they have the same M-dimension. The M-dimension is additive, and a module is isomorphic to a subspace of another module if and only if it has smaller or equal M-dimension.A module is called standard if it has a cyclic separating vector. Each factor has a standard representation, which is unique up to isomorphism. The standard representation has an antilinear involution J such that JMJ = M′.
For finite factors the standard module is given by the GNS construction applied to the unique normal tracial state and the M-dimension is normalized so that the standard module has M-dimension 1, while for infinite factors the standard module is the module with M-dimension equal to ∞.
The possible M-dimensions of modules are given as follows:
- Type In (n finite): The M-dimension can be any of 0/n, 1/n, 2/n, 3/n, ..., ∞. The standard module has M-dimension 1 (and complex dimension n2.)
- Type I∞ The M-dimension can be any of 0, 1, 2, 3, ..., ∞. The standard representation of B(H) is H⊗H; its M-dimension is ∞.
- Type II1: The M-dimension can be anything in [0, ∞]. It is normalized so that the standard module has M-dimension 1. The M-dimension is also called the coupling constant of the module H.
- Type II∞: The M-dimension can be anything in [0, ∞]. There is in general no canonical way to normalize it; the factor may have outer automorphisms multiplying the M-dimension by constants. The standard representation is the one with M-dimension ∞.
- Type III: The M-dimension can be 0 or ∞. Any two non-zero modules are isomorphic, and all non-zero modules are standard.
Amenable von Neumann algebras
and others proved that the following conditions on a von Neumann algebra Mon a separable Hilbert space H are all equivalent:
- M is hyperfinite or AFD or approximately finite dimensional or approximately finite: this means the algebra contains an ascending sequence of finite dimensional subalgebras with dense union. (Warning: some authors use "hyperfinite" to mean "AFD and finite".)
- M is amenable: this means that the derivationDerivation (abstract algebra)In abstract algebra, a derivation is a function on an algebra which generalizes certain features of the derivative operator. Specifically, given an algebra A over a ring or a field K, a K-derivation is a K-linear map D: A → A that satisfies Leibniz's law: D = b + a.More...
s of M with values in a normal dual Banach bimodule are all inner.
- M has Schwartz's property P: for any bounded operator T on H the weak operator closed convex hull of the elements uTu* contains an element commuting with M.
- M is semidiscrete: this means the identity map from M to M is a weak pointwise limit of completely positive maps of finite rank.
- M has property E or the Hakeda-Tomiyama extension property: this means that there is a projection of norm 1 from bounded operators on H to M '.
- M is injective: any completely positive linear map from any self adjoint closed subspace containing 1 of any unital C*-algebra A to M can be extended to a completely positive map from A to M.
There is no generally accepted term for the class of algebras above; Connes has suggested that amenable should be the standard term.
The amenable factors have been classified: there is a unique one of each of the types In, I∞, II1, II∞, IIIλ,
for 0<λ≤ 1, and the ones of type III0 correspond to certain ergodic
flows. (For type III0 calling this a classification is a little misleading, as it is known that there is no easy way to classify the corresponding ergodic flows.) The ones of type I and II1 were classified by , and the remaining ones were classified by , except for the type III1 case
which was completed by Haagerup.
All amenable factors can be constructed using the group-measure space construction
Crossed product
In mathematics, and more specifically in the theory of von Neumann algebras, a crossed productis a basic method of constructing a new von Neumann algebra froma von Neumann algebra acted on by a group. It is related to...
of Murray and von Neumann for a single ergodic transformation. In fact they are precisely the factors arising as crossed product
Crossed product
In mathematics, and more specifically in the theory of von Neumann algebras, a crossed productis a basic method of constructing a new von Neumann algebra froma von Neumann algebra acted on by a group. It is related to...
s by free ergodic actions of Z or Zn on abelian von Neumann algebras L∞(X). Type I factors occur when the measure space X is atomic
Atom (measure theory)
In mathematics, more precisely in measure theory, an atom is a measurable set which has positive measure and contains no set of smaller but positive measure...
and the action transitive. When X is diffuse or non-atomic
Atom (measure theory)
In mathematics, more precisely in measure theory, an atom is a measurable set which has positive measure and contains no set of smaller but positive measure...
, it is equivalent
Equivalence (measure theory)
In mathematics, and specifically in measure theory, equivalence is a notion of two measures being "the same".-Definition:Let be a measurable space, and let μ, ν : Σ → R be two signed measures. Then μ is said to be equivalent to ν if and only if each is absolutely continuous with respect to the other...
to [0,1] as a measure space. Type II factors occur when X admits an equivalent
Equivalence (measure theory)
In mathematics, and specifically in measure theory, equivalence is a notion of two measures being "the same".-Definition:Let be a measurable space, and let μ, ν : Σ → R be two signed measures. Then μ is said to be equivalent to ν if and only if each is absolutely continuous with respect to the other...
finite (II1) or infinite (II∞,) measure, invariant under an action of
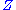 . Type III factors occur in the remaining cases where there is no invariant measure, but only an invariant measure class
. Type III factors occur in the remaining cases where there is no invariant measure, but only an invariant measure classQuasi-invariant measure
In mathematics, a quasi-invariant measure μ with respect to a transformation T, from a measure space X to itself, is a measure which, roughly speaking, is multiplied by a numerical function by T...
: these factors are called Krieger factors.
Tensor products of von Neumann algebras
The Hilbert space tensor product of two Hilbert spaces is the completion of their algebraic tensor product.One can define a tensor product of von Neumann algebras (a completion of the algebraic tensor product of the algebras considered as rings), which is again a von Neumann algebra, and act on the tensor product of the corresponding Hilbert spaces. The tensor product of two finite algebras is finite, and the tensor product of an infinite algebra and a non-zero algebra is infinite. The type of the tensor product of two von Neumann algebras (I, II, or III) is the maximum of their types. The commutation theorem for tensor products states that
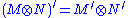
(where M′ denotes the commutant of M).
The tensor product of an infinite number of von Neumann algebras, if done naively, is usually a ridiculously large non-separable algebra. Instead showed that one should choose a state on each of the von Neumann algebras, use this to define a state on the algebraic tensor product, which can be used to product a Hilbert space and a (reasonably small) von Neumann algebra. studied the case where all the factors are finite matrix algebras; these factors are called Araki-Woods factors or ITPFI factors (ITPFI stands for "infinite tensor product of finite type I factors"). The type of the infinite tensor product can vary dramatically as the states are changed; for example, the infinite tensor product of an infinite number of type I2 factors can have any type depending on the choice of states. In particular found an uncountable family of non-isomorphic hyperfinite type IIIλ factors for 0<λ<1, called Powers factors, by taking an infinite tensor product of
type I2 factors, each with the state given by :
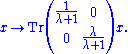
All hyperfinite von Neumann algebras not of type III0 are isomorphic to Araki-Woods factors, but there are uncountably many of type III0 that are not.
Bimodules and subfactors
Abimodule
(or correspondence) is a Hilbert space H with module actions of two commuting von Neumann algebras. Bimodules have a much richer structure than that of modules. Any bimodule over two factors always gives a subfactor
Subfactor
In the theory of von Neumann algebras, a subfactor of a factor M is a subalgebra that is a factor and contains 1. The theory of subfactors led to the discovery of theJones polynomial in knot theory.-Index of a subfactor:...
since one of the factors is always contained in the commutant of the other. There is also a subtle relative tensor product operation due to Connes
Alain Connes
Alain Connes is a French mathematician, currently Professor at the Collège de France, IHÉS, The Ohio State University and Vanderbilt University.-Work:...
on bimodules. The theory of subfactor
Subfactor
In the theory of von Neumann algebras, a subfactor of a factor M is a subalgebra that is a factor and contains 1. The theory of subfactors led to the discovery of theJones polynomial in knot theory.-Index of a subfactor:...
s, initiated by Vaughan Jones
Vaughan Jones
Sir Vaughan Frederick Randal Jones, KNZM, FRS, FRSNZ is a New Zealand mathematician, known for his work on von Neumann algebras, knot polynomials and conformal field theory. He was awarded a Fields Medal in 1990, and famously wore a New Zealand rugby jersey when he accepted the prize...
, reconciles these two seemingly different points of view.
Bimodules are also important for the von Neumann group algebra M of a discrete group
 . Indeed if V is any unitary representation
. Indeed if V is any unitary representationUnitary representation
In mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
of
 , then, regarding
, then, regarding  as the diagonal subgroup of
as the diagonal subgroup of 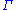 x
x 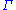 , the corresponding induced representation
, the corresponding induced representationInduced representation
In mathematics, and in particular group representation theory, the induced representation is one of the major general operations for passing from a representation of a subgroup H to a representation of the group G itself. It was initially defined as a construction by Frobenius, for linear...
on l2 (
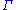 ,V) is naturally a bimodule for two commuting copies of M. Important representation theoretic
,V) is naturally a bimodule for two commuting copies of M. Important representation theoreticRepresentation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
properties of
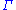 can be formulated entirely in terms of bimodules and therefore make sense for the von Neumann algebra itself. For example Connes
can be formulated entirely in terms of bimodules and therefore make sense for the von Neumann algebra itself. For example ConnesAlain Connes
Alain Connes is a French mathematician, currently Professor at the Collège de France, IHÉS, The Ohio State University and Vanderbilt University.-Work:...
and Jones
Vaughan Jones
Sir Vaughan Frederick Randal Jones, KNZM, FRS, FRSNZ is a New Zealand mathematician, known for his work on von Neumann algebras, knot polynomials and conformal field theory. He was awarded a Fields Medal in 1990, and famously wore a New Zealand rugby jersey when he accepted the prize...
gave a definition of an analogue of Kazhdan's Property T for von Neumann algebras in this way.
Non-amenable factors
Von Neumann algebras of type I are always amenable, but for the other types there are an uncountable number of different non-amenable factors, which seem very hard to classify, or even distinguish from each other. Nevertheless VoiculescuDan-Virgil Voiculescu
Dan-Virgil Voiculescu is a professor of mathematics at the University of California, Berkeley. He has worked in single operator theory, operator K-theory and von Neumann algebras. More recently, he developed free probability theory....
has shown that the class of non-amenable factors coming from the group-measure space construction is disjoint from the class coming from group von Neumann algebras of free groups. Later Narutaka Ozawa proved that group von Neumann algebras of hyperbolic group
Hyperbolic group
In group theory, a hyperbolic group, also known as a word hyperbolic group, Gromov hyperbolic group, negatively curved group is a finitely generated group equipped with a word metric satisfying certain properties characteristic of hyperbolic geometry. The notion of a hyperbolic group was introduced...
s yield prime
Prime
A prime is a natural number that has exactly two distinct natural number divisors: 1 and itself.Prime or PRIME may also refer to:In mathematics:*Prime , the ′ mark, typically used as a suffix...
type II1 factors, i.e. ones that cannot be factored as tensor products of type II1 factors, a result first proved by Leeming Ge for free group factors using Voiculescu's free entropy.
Popa's work on fundamental groups of non-amenable factors represents another significant advance. The theory of factors "beyond the hyperfinite" is rapidly expanding at present, with many new and surprising results; it has close links with rigidity phenomena
Grigory Margulis
Gregori Aleksandrovich Margulis is a Russian mathematician known for his far-reaching work on lattices in Lie groups, and the introduction of methods from ergodic theory into diophantine approximation. He was awarded a Fields Medal in 1978 and a Wolf Prize in Mathematics in 2005, becoming the...
in geometric group theory
Geometric group theory
Geometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups act .Another important...
and ergodic theory
Ergodic theory
Ergodic theory is a branch of mathematics that studies dynamical systems with an invariant measure and related problems. Its initial development was motivated by problems of statistical physics....
.
Examples
- The essentially bounded functions on a σ-finite measure space form a commutative (type I1) von Neumann algebra acting on the L2 functions. For certain non-σ-finite measure spaces, usually considered pathologicalPathological (mathematics)In mathematics, a pathological phenomenon is one whose properties are considered atypically bad or counterintuitive; the opposite is well-behaved....
, L∞(X) is not a von Neumann algebra; for example, the σ-algebra of measurable sets might be the countable-cocountable algebra on an uncountable set.
- The bounded operators on any Hilbert space form a von Neumann algebra, indeed a factor, of type I.
- If we have any unitary representationUnitary representationIn mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
of a group G on a Hilbert space H then the bounded operators commuting with G form a von Neumann algebra G′, whose projections correspond exactly to the closed subspaces of H invariant under G. Equivalent subrepresentations correspond to equivalent projections in G′. The double commutant G′′ of G is also a von Neumann algebra.
- The von Neumann group algebra of a discrete group G is the algebra of all bounded operators on H = l2(G) commuting with the action of G on H through right multiplication. One can show that this is the von Neumann algebra generated by the operators corresponding to multiplication from the left with an element g ∈ G. It is a factor (of type II1) if every non-trivial conjugacy class of G is infinite (for example, a non-abelian free group), and is the hyperfinite factor of type II1 if in addition G is a union of finite subgroups (for example, the group of all permutations of the integers fixing all but a finite number of elements).
- The tensor product of two von Neumann algebras, or of a countable number with states, is a von Neumann algebra as described in the section above.
- The crossed productCrossed productIn mathematics, and more specifically in the theory of von Neumann algebras, a crossed productis a basic method of constructing a new von Neumann algebra froma von Neumann algebra acted on by a group. It is related to...
of a von Neumann algebra by a discrete (or more generally locally compact) group can be defined, and is a von Neumann algebra. Special cases are the group-measure space construction of Murray and von Neumann and Krieger factors.
- The von Neumann algebras of a measurable equivalence relationEquivalence relationIn mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
and a measurable groupoidGroupoidIn mathematics, especially in category theory and homotopy theory, a groupoid generalises the notion of group in several equivalent ways. A groupoid can be seen as a:...
can be defined. These examples generalise von Neumann group algebras and the group-measure space construction.
Applications
Von Neumann algebras have found applications in diverse areas of mathematics like knot theoryKnot theory
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...
, statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
, Quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
, Local quantum physics, Free probability
Free probability
Free probability is a mathematical theory that studies non-commutative random variables. The "freeness" or free independence property is the analogue of the classical notion of independence, and it is connected with free products....
, Noncommutative geometry
Noncommutative geometry
Noncommutative geometry is a branch of mathematics concerned with geometric approach to noncommutative algebras, and with construction of spaces which are locally presented by noncommutative algebras of functions...
, representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
, geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, and probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
.

