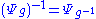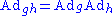Adjoint representation
Encyclopedia
In mathematics
, the adjoint representation (or adjoint action) of a Lie group
G is the natural representation
of G on its own Lie algebra
. This representation is the linearized version of the action
of G on itself by conjugation.
and let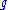
be its Lie algebra
(which we identify with TeG, the tangent space
to the identity element
in G). Define a map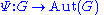
by the equation
for all g in G, where 
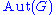is the automorphism group of G and the automorphism
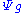is defined by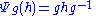
for all h in G. It follows that the derivative of Ψg at the identity is an automorphism of the Lie algebra
.
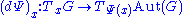
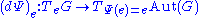
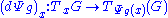
We denote this map by Adg: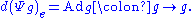
To say that Adg is a Lie algebra automorphism is to say that Adg is a linear transformation
of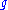
that preserves the Lie bracket
. The map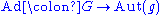
which sends g to Adg is called the adjoint representation of G. This is indeed a representation
of G since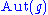
is a Lie subgroup
of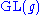
and the above adjoint map is a Lie group homomorphism. The dimension of the adjoint representation is the same as the dimension of the group G.
by taking the derivative at the identity.
Taking the derivative of the adjoint map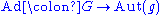
gives the adjoint representation of the Lie algebra
:
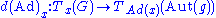
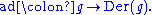
Here
is the Lie algebra of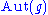 
which may be identified with the derivation algebra of 
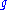. The adjoint representation of a Lie algebra is related in a fundamental way to the structure of that algebra. In particular, one can show that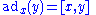
for all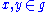
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the adjoint representation (or adjoint action) of a Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
G is the natural representation
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
of G on its own Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
. This representation is the linearized version of the action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
of G on itself by conjugation.
Formal definition
Let G be a Lie groupLie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
and let
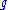be its Lie algebraLie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
(which we identify with TeG, the tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
to the identity element
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
in G). Define a map
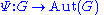
by the equation
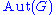for all g in G, where is the automorphism group of G and the automorphismAutomorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
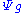is defined by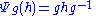for all h in G. It follows that the derivative of Ψg at the identity is an automorphism of the Lie algebra
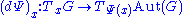
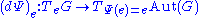
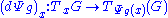
.We denote this map by Adg:
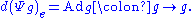
To say that Adg is a Lie algebra automorphism is to say that Adg is a linear transformation
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
of
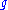that preserves the Lie bracketLie bracket
Lie bracket can refer to:*A bilinear binary operation defined on elements of a Lie algebra*Lie bracket of vector fields...
. The map
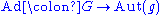
which sends g to Adg is called the adjoint representation of G. This is indeed a representation
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
of G since
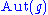is a Lie subgroupLie subgroup
In mathematics, a Lie subgroup H of a Lie group G is a Lie group that is a subset of G and such that the inclusion map from H to G is an injective immersion and group homomorphism. According to Cartan's theorem, a closed subgroup of G admits a unique smooth structure which makes it an embedded Lie...
of
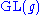and the above adjoint map is a Lie group homomorphism. The dimension of the adjoint representation is the same as the dimension of the group G.Adjoint representation of a Lie algebra
One may always pass from a representation of a Lie group G to a representation of its Lie algebraRepresentation of a Lie algebra
In the mathematical field of representation theory, a Lie algebra representation or representation of a Lie algebra is a way of writing a Lie algebra as a set of matrices in such a way that the Lie bracket is given by the commutator.The notion is closely related to that of a representation of a...
by taking the derivative at the identity.
Taking the derivative of the adjoint map
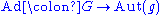
gives the adjoint representation of the Lie algebra
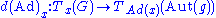
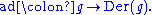
:Here
is the Lie algebra of 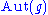which may be identified with the derivation algebra of 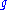. The adjoint representation of a Lie algebra is related in a fundamental way to the structure of that algebra. In particular, one can show that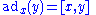for all
.-
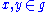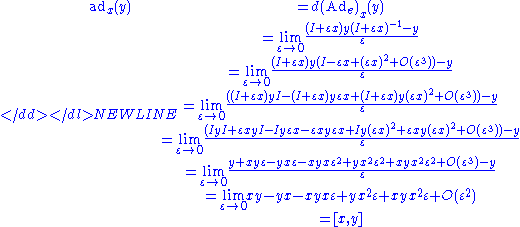
Examples
- If G is abelianAbelian groupIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
of dimension n, the adjoint representation of G is the trivial n-dimensional representation. - If G is a matrix Lie group (i.e. a closed subgroup of GL(n,C)), then its Lie algebra is an algebra of n×n matrices with the commutator for a Lie bracket (i.e. a subalgebra of
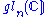). In this case, the adjoint map is given by Adg(x) = gxg−1. - If G is SL2(R) (real 2×2 matrices with determinantDeterminantIn linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
1), the Lie algebra of G consists of real 2×2 matrices with traceTrace (linear algebra)In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
0. The representation is equivalent to that given by the action of G by linear substitution on the space of binary (i.e., 2 variable) quadratic formQuadratic formIn mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
s.
Properties
The following table summarizes the properties of the various maps mentioned in the definition
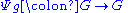
Lie group homomorphism:
Lie group automorphism:
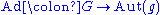
Lie group homomorphism:
Lie algebra automorphism:
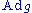is linear
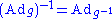
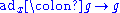
Lie algebra homomorphism:
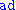is linear
Lie algebra derivation:
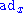is linear
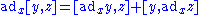
The imageImage (mathematics)In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
of G under the adjoint representation is denoted by AdG. If G is connectedConnected spaceIn topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
, the kernel of the adjoint representation coincides with the kernel of Ψ which is just the centerCenter (group theory)In abstract algebra, the center of a group G, denoted Z,The notation Z is from German Zentrum, meaning "center". is the set of elements that commute with every element of G. In set-builder notation,...
of G. Therefore the adjoint representation of a connected Lie group G is faithfulFaithful representationIn mathematics, especially in the area of abstract algebra known as representation theory, a faithful representation ρ of a group G on a vector space V is a linear representation in which different elements g of G are represented by distinct linear mappings ρ.In more abstract language, this means...
if and only if G is centerless. More generally, if G is not connected, then the kernel of the adjoint map is the centralizer of the identity componentIdentity componentIn mathematics, the identity component of a topological group G is the connected component G0 of G that contains the identity element of the group...
G0 of G. By the first isomorphism theorem we have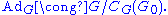
Roots of a semisimple Lie group
If G is semisimple, the non-zero weightsWeight (representation theory)In the mathematical field of representation theory, a weight of an algebra A over a field F is an algebra homomorphism from A to F – a linear functional – or equivalently, a one dimensional representation of A over F. It is the algebra analogue of a multiplicative character of a group...
of the adjoint representation form a root systemRoot systemIn mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras...
. To see how this works, consider the case G = SLn(R).
We can take the group of diagonal matrices diag(t1, ..., tn) as our maximal torusMaximal torusIn the mathematical theory of compact Lie groups a special role is played by torus subgroups, in particular by the maximal torus subgroups.A torus in a Lie group G is a compact, connected, abelian Lie subgroup of G . A maximal torus is one which is maximal among such subgroups...
T. Conjugation by an element of T sends
Thus, T acts trivially on the diagonal part of the Lie algebra of G and with eigenvectors titj−1 on the various off-diagonal entries. The roots of G are the weights
diag(t1, ..., tn)→titj−1. This accounts for the standard description of the root system of G = SLn(R) as the set of vectors of the form ei−ej.
Example SL2(R)
Let us compute the root system for one of the simplest cases of Lie Groups. Let us consider the group SL2(R) of two dimensional matrices with determinant 1. This consists of the set of matrices of the form:
-
with a, b, c, d real and ad − bc = 1.
A maximal compact connected abelian Lie subgroup, or maximal torus T, is given by the subset of all matrices of the form
-
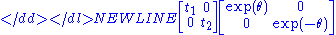
with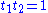
. The Lie algebra of the maximal torus is the Cartan subalgebra consisting of the matrices
-
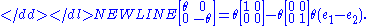
If we conjugate an element of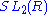
by an element of the maximal torus we obtain
-
The matrices
-
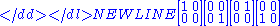
are then 'eigenvectors' of the conjugation operation with eigenvalues
. The function 
which gives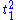 
is a multiplicative character, or homomorphism from the group's torus to the underlying field R. The function 
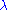giving 
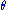is a weight of the Lie Algebra with weight space given by the span of the matrices.
It is satisfying to show the multiplicativity of the character and the linearity of the weight. It can further be proved that the differential of
can be used to create a weight. It is also educational to consider the case of SL3(R).
Variants and analogues
The adjoint representation can also be defined for algebraic groupAlgebraic groupIn algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety...
s over any field.
The co-adjoint representation is the contragredient representation of the adjoint representation. Alexandre KirillovAlexandre KirillovAlexandre Aleksandrovich Kirillov is a Soviet and Russian mathematician, renowned for his works in the fields of representation theory, topological groups and Lie groups. In particular he introduced the orbit method into representation theory....
observed that the orbit of any vector in a co-adjoint representation is a symplectic manifoldSymplectic manifoldIn mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
. According to the philosophy in representation theoryRepresentation theoryRepresentation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
known as the orbit method (see also the Kirillov character formulaKirillov character formulaIn mathematics, for a Lie group G, the Kirillov orbit method gives a heuristic method in representation theory. It connects the Fourier transforms of coadjoint orbits, which lie in the dual space of the Lie algebra of G, to the infinitesimal characters of the irreducible representations...
), the irreducible representations of a Lie group G should be indexed in some way by its co-adjoint orbits. This relationship is closest in the case of nilpotent Lie groups.
-
-
-
-
- If G is abelian
