Elementary Abelian group
Encyclopedia
In group theory
, an elementary abelian group is a finite abelian group
, where every nontrivial element has order p, where p is a prime; in particular it is a p-group
.
By the classification of finitely generated abelian groups, every elementary abelian group must be of the form
n
for n a non-negative integer (sometimes called the group's rank). Here, Z/pZ denotes the cyclic group
of order p (or equivalently the integers mod
p), and the notation means the n-fold Cartesian product.
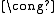(Z/pZ)n is an elementary abelian group. Since Z/pZ 
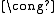Fp, the finite field
of p elements, we have V = (Z/pZ)n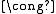
Fpn, hence V can be considered as an n-dimensional vector space
over the field Fp. Note that an elementary abelian group does not in general have a distinguished basis: choice of isomorphism V
(Z/pZ)n corresponds to a choice of basis.
To the observant reader, it may appear that Fpn has more structure than the group V, in particular that it has scalar multiplication in addition to (vector/group) addition. However, V as an abelian group has a unique Z-module
structure where the action of Z corresponds to repeated addition, and this Z-module structure is consistent with the Fp scalar multiplication. That is, c·g = g + g + ... + g (c times) where c in Fp (considered as an integer with 0 ≤ c < p) gives V a natural Fp-module structure.
we have that the mapping T(ei) = vi extends uniquely to a linear transformation of V. Each such T can be considered as a group homomorphism from V to V (an endomorphism
) and likewise any endomorphism of V can be considered as a linear transformation of V as a vector space.
If we restrict our attention to automorphism
s of V we have Aut(V) = { T : V → V | ker T = 0 } = GLn(Fp), the general linear group
of n × n invertible matrices on Fp.
s are extensions of elementary abelian groups by a cyclic group of order p, and are analogous to the Heisenberg group.
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, an elementary abelian group is a finite abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
, where every nontrivial element has order p, where p is a prime; in particular it is a p-group
P-group
In mathematics, given a prime number p, a p-group is a periodic group in which each element has a power of p as its order: each element is of prime power order. That is, for each element g of the group, there exists a nonnegative integer n such that g to the power pn is equal to the identity element...
.
By the classification of finitely generated abelian groups, every elementary abelian group must be of the form
n
for n a non-negative integer (sometimes called the group's rank). Here, Z/pZ denotes the cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
of order p (or equivalently the integers mod
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
p), and the notation means the n-fold Cartesian product.
Examples and properties
- The elementary abelian group (Z/2Z)2 has four elements: { (0,0), (0,1), (1,0), (1,1) }. Addition is performed componentwise, taking the result mod 2. For instance, (1,0) + (1,1) = (0,1).
- (Z/pZ)n is generated by n elements, and n is the least possible number of generators. In particular, the set {e1, ..., en}, where ei has a 1 in the ith component and 0 elsewhere, is a minimal generating set.
- Every elementary abelian group has a fairly simple finite presentationPresentation of a groupIn mathematics, one method of defining a group is by a presentation. One specifies a set S of generators so that every element of the group can be written as a product of powers of some of these generators, and a set R of relations among those generators...
.
-
- (Z/pZ)n
< e1, ..., en | eip = 1, eiej = ejei >
- (Z/pZ)n
Vector space structure
Suppose V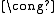 (Z/pZ)n is an elementary abelian group. Since Z/pZ 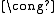Fp, the finite fieldFinite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
of p elements, we have V = (Z/pZ)n
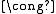Fpn, hence V can be considered as an n-dimensional vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
over the field Fp. Note that an elementary abelian group does not in general have a distinguished basis: choice of isomorphism V
(Z/pZ)n corresponds to a choice of basis.To the observant reader, it may appear that Fpn has more structure than the group V, in particular that it has scalar multiplication in addition to (vector/group) addition. However, V as an abelian group has a unique Z-module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
structure where the action of Z corresponds to repeated addition, and this Z-module structure is consistent with the Fp scalar multiplication. That is, c·g = g + g + ... + g (c times) where c in Fp (considered as an integer with 0 ≤ c < p) gives V a natural Fp-module structure.
Automorphism group
As a vector space V has a basis {e1, ..., en} as described in the examples. If we take {v1, ..., vn} to be any n elements of V, then by linear algebraLinear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
we have that the mapping T(ei) = vi extends uniquely to a linear transformation of V. Each such T can be considered as a group homomorphism from V to V (an endomorphism
Endomorphism
In mathematics, an endomorphism is a morphism from a mathematical object to itself. For example, an endomorphism of a vector space V is a linear map ƒ: V → V, and an endomorphism of a group G is a group homomorphism ƒ: G → G. In general, we can talk about...
) and likewise any endomorphism of V can be considered as a linear transformation of V as a vector space.
If we restrict our attention to automorphism
Automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
s of V we have Aut(V) = { T : V → V | ker T = 0 } = GLn(Fp), the general linear group
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
of n × n invertible matrices on Fp.
A generalisation to higher orders
It can also be of interest to go beyond prime order components to prime-power order. Consider an elementary abelian group G to be of type (p,p,...,p) for some prime p. A homocyclic group (of rank n) is an abelian group of type (pe,pe,...,pe) i.e. the direct product of n isomorphic groups of order pe.Related groups
The extra special groupExtra special group
In group theory, a branch of mathematics, extra special groups are analogues of the Heisenberg group over finite fields whose size is a prime. For each prime p and positive integer n there are exactly two extra special groups of order p1+2n. Extra special groups often occur in centralizers of...
s are extensions of elementary abelian groups by a cyclic group of order p, and are analogous to the Heisenberg group.