Maximal torus
Encyclopedia
In the mathematical
theory of compact Lie groups a special role is played by torus
subgroups, in particular by the maximal torus subgroups.
A torus in a Lie group
G is a compact
, connected
, abelian
Lie subgroup
of G (and therefore isomorphic to the standard torus Tn). A maximal torus is one which is maximal among such subgroups. That is, T is a maximal torus if for any other torus T′ containing T we have T = T′. Every torus is contained in a maximal torus simply by dimensional considerations. A noncompact Lie group need not have any nontrivial tori (e.g. Rn).
The dimension of a maximal torus in G is called the rank of G. The rank is well-defined
since all maximal tori turn out to be conjugate. For semisimple groups the rank is equal to the number of nodes in the associated Dynkin diagram.
U(n) has as a maximal torus the subgroup of all diagonal matrices. That is,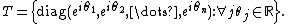
T is clearly isomorphic to the product of n circles, so the unitary group U(n) has rank n. A maximal torus in the special unitary group
SU(n) ⊂ U(n) is just the intersection of T and SU(n) which is a torus of dimension n − 1.
A maximal torus in special orthogonal group SO(2n) is a given by the set of all simultaneous rotation
s in n pairwise orthogonal 2-planes. This is also a maximal torus in the group SO(2n+1) where the action fixes the remaining direction. Therefore, both SO(2n) and SO(2n+1) have rank n. For example, in the rotation group
SO(3) the maximal tori are given by rotations about a fixed axis.
The symplectic group
Sp(n) has rank n. A maximal torus is given by the set of all diagonal matrices whose entries all lie in a fixed complex subalgebra of H.
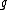be the Lie algebra
of G.
of G with respect to T can be defined as the normalizer of T modulo the centralizer of T. That is,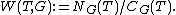
Fix a maximal torus 
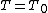in G; then the corresponding Weyl group is called the Weyl group of G (it depends up to isomorphism on the choice of T). The representation theory
of G is essentially determined by T and W.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
theory of compact Lie groups a special role is played by torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
subgroups, in particular by the maximal torus subgroups.
A torus in a Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
G is a compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
, connected
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
, abelian
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
Lie subgroup
Lie subgroup
In mathematics, a Lie subgroup H of a Lie group G is a Lie group that is a subset of G and such that the inclusion map from H to G is an injective immersion and group homomorphism. According to Cartan's theorem, a closed subgroup of G admits a unique smooth structure which makes it an embedded Lie...
of G (and therefore isomorphic to the standard torus Tn). A maximal torus is one which is maximal among such subgroups. That is, T is a maximal torus if for any other torus T′ containing T we have T = T′. Every torus is contained in a maximal torus simply by dimensional considerations. A noncompact Lie group need not have any nontrivial tori (e.g. Rn).
The dimension of a maximal torus in G is called the rank of G. The rank is well-defined
Well-defined
In mathematics, well-definition is a mathematical or logical definition of a certain concept or object which uses a set of base axioms in an entirely unambiguous way and satisfies the properties it is required to satisfy. Usually definitions are stated unambiguously, and it is clear they satisfy...
since all maximal tori turn out to be conjugate. For semisimple groups the rank is equal to the number of nodes in the associated Dynkin diagram.
Examples
The unitary groupUnitary group
In mathematics, the unitary group of degree n, denoted U, is the group of n×n unitary matrices, with the group operation that of matrix multiplication. The unitary group is a subgroup of the general linear group GL...
U(n) has as a maximal torus the subgroup of all diagonal matrices. That is,
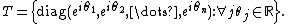
T is clearly isomorphic to the product of n circles, so the unitary group U(n) has rank n. A maximal torus in the special unitary group
Special unitary group
The special unitary group of degree n, denoted SU, is the group of n×n unitary matrices with determinant 1. The group operation is that of matrix multiplication...
SU(n) ⊂ U(n) is just the intersection of T and SU(n) which is a torus of dimension n − 1.
A maximal torus in special orthogonal group SO(2n) is a given by the set of all simultaneous rotation
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
s in n pairwise orthogonal 2-planes. This is also a maximal torus in the group SO(2n+1) where the action fixes the remaining direction. Therefore, both SO(2n) and SO(2n+1) have rank n. For example, in the rotation group
Rotation group
In mechanics and geometry, the rotation group is the group of all rotations about the origin of three-dimensional Euclidean space R3 under the operation of composition. By definition, a rotation about the origin is a linear transformation that preserves length of vectors and preserves orientation ...
SO(3) the maximal tori are given by rotations about a fixed axis.
The symplectic group
Symplectic group
In mathematics, the name symplectic group can refer to two different, but closely related, types of mathematical groups, denoted Sp and Sp. The latter is sometimes called the compact symplectic group to distinguish it from the former. Many authors prefer slightly different notations, usually...
Sp(n) has rank n. A maximal torus is given by the set of all diagonal matrices whose entries all lie in a fixed complex subalgebra of H.
Properties
Let G be a compact, connected Lie group and let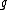 be the Lie algebraLie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
of G.
- A maximal torus in G is a maximal abelian subgroup, but the converse need not hold.
- The maximal tori in G are exactly the Lie subgroups corresponding to the maximal abelian, diagonally acting subalgebras of
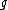(cf. Cartan subalgebra) - Given a maximal torus T in G, every element g ∈ G is conjugate to an element in T.
- Since the conjugate of a maximal torus is a maximal torus, every element of G lies in some maximal torus.
- All maximal tori in G are conjugate. Therefore, the maximal tori form a single conjugacy classConjugacy classIn mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...
among the subgroups of G. - It follows that the dimensions of all maximal tori are the same. This dimension is the rank of G.
- If G has dimension n and rank r then n − r is even.
Weyl group
Given a torus T (not necessarily maximal), the Weyl groupWeyl group
In mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection...
of G with respect to T can be defined as the normalizer of T modulo the centralizer of T. That is,
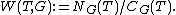Fix a maximal torus 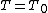in G; then the corresponding Weyl group is called the Weyl group of G (it depends up to isomorphism on the choice of T). The representation theoryRepresentation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
of G is essentially determined by T and W.
- The Weyl group acts by (outer) automorphismAutomorphismIn mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
s on T (and its Lie algebra). - The centralizer of T in G is equal to T, so the Weyl group is equal to N(T)/T.
- The identity componentIdentity componentIn mathematics, the identity component of a topological group G is the connected component G0 of G that contains the identity element of the group...
of the normalizer of T is also equal T. The Weyl group is therefore equal to the component group of N(T). - The normalizer of T is closedClosed setIn geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
, so the Weyl group is finite - Two elements in T are conjugate if and only if they are conjugate by an element of W. That is, the conjugacy classes of G intersect T in a Weyl orbit.
- The space of conjugacy classes in G is diffeomorphic to the orbit space T/W.