
Tempered representation
Encyclopedia
In mathematics, a tempered representation of a linear semisimple Lie group is a representation
that has a basis whose matrix coefficient
s lie in the Lp space
for any ε > 0.
which would be the definition of a discrete series representation
. If G is a linear semisimple Lie group with a maximal compact subgroup K, an admissible representation
ρ of G is tempered if the above condition holds for the K-finite
matrix coefficients of ρ.
The definition above is also used for more general groups, such as p-adic Lie groups and finite central extensions of semisimple real algebraic groups. The definition of "tempered representation" makes sense for arbitrary unimodular locally compact group
s, but on groups with infinite centers such as infinite central extensions of semisimple Lie groups it does not behave well and is usually replaced by a slightly different definition.
Tempered representations on semisimple Lie groups were first defined and studied by Harish-Chandra
(using a different but equivalent definition), who showed that they are exactly the representations needed for the Plancherel theorem
. They were classified by Knapp and Zuckerman, and used by Langlands in the Langlands classification
of irreducible representations of a reductive Lie group G in terms of the tempered representations of smaller groups.
in his work on harmonic analysis on a semisimple Lie group as those representations that contribute to the Plancherel measure
. The original definition of a tempered representation, which has certain technical advantages, is that its Harish-Chandra character
should be a "tempered distribution" (see the section about this below). It follows from Harish-Chandra's results that it is equivalent to the more elementary definition given above. Tempered representations also seem to play a fundamental role in the theory of automorphic form
s. This connection was probably first realized by Satake (in the context of the Ramanujan-Petersson conjecture) and Robert Langlands
and served as a motivation for Langlands to develop his classification scheme
for irreducible admissible representations of real and p-adic reductive algebraic groups in terms of the tempered representations of smaller groups. The precise conjectures identifying the place of tempered representations in the automorphic spectrum were formulated later by James Arthur
and constitute one of the most actively developing parts of the modern theory of automorphic forms.
representation of a semisimple Lie group G is tempered if and only if it is in the support of the Plancherel measure
of G. In other words, tempered representations are precisely the class of representations of G appearing in the spectral decomposition of L2 functions on the group (while discrete series representations have a stronger property that an individual representation has a positive spectral measure). This stands in contrast with the situation for abelian and more general solvable Lie groups, where a different class of representations is needed to fully account for the spectral decomposition. This can be seen already in the simplest example of the additive group R of the real numbers, for which the matrix elements of the irreducible representations do not fall off to 0 at infinity.
In the Langlands program
, tempered representations of real Lie groups are those coming from unitary characters of tori by Langlands functoriality.
In fact they classified a more general class of representations called basic representations. If P=MAN is the Langlands decomposition
of a cuspidal parabolic subgroup, then a basic representation is defined to be
the parabolically induced representation associated to a limit of discrete series representation of M and a unitary representation of the abelian group A. If the limit of discrete series representation is in fact a discrete series representation, then the basic representation is called an induced discrete series representation. Any irreducible tempered representation is a basic representation, and conversely any basic representation is the sum of a finite number of irreducible tempered representations. More precisely, it is a direct sum of 2r irreducible tempered representations indexed by the characters of an elementary abelian group R of order 2r (called the R-group).
Any basic representation, and consequently any irreducible tempered representation, is a summand of an induced discrete series representation. However it is not always possible to represent an irreducible tempered representation as an induced discrete series representation, which is why one considers the more general class of basic representations.
So the irreducible tempered representations are just the irreducible basic representations, and can be classified by listing all basic representations and picking out those that are irreducible, in other words those that have trivial R-group.
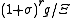
is bounded.
Here Ξ is a certain spherical function on G, invariant under left and right multiplication by K,
and σ is the norm of the log of p, where an element g of G is written as : g=kp
for k in K and p in P.
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
that has a basis whose matrix coefficient
Matrix coefficient
In mathematics, a matrix coefficient is a function on agroup of a special form, which depends on a linear representation of the group and additional data...
s lie in the Lp space
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
- L2+ε(G)
for any ε > 0.
Formulation
This condition, as just given, is slightly weaker than the condition that the matrix coefficients are square-integrable, in other words lie in- L2(G),
which would be the definition of a discrete series representation
Discrete series representation
In mathematics, a discrete series representation is an irreducible unitary representation of a locally compact topological group G that is a subrepresentation of the left regular representation of G on L²...
. If G is a linear semisimple Lie group with a maximal compact subgroup K, an admissible representation
Admissible representation
In mathematics, admissible representations are a well-behaved class of representations used in the representation theory of reductive Lie groups and locally compact totally disconnected groups. They were introduced by Harish-Chandra....
ρ of G is tempered if the above condition holds for the K-finite
K-finite
In mathematics, a K-finite function is a type of generalized trigonometric polynomial. Here K is some compact group, and the generalization is from the circle group T....
matrix coefficients of ρ.
The definition above is also used for more general groups, such as p-adic Lie groups and finite central extensions of semisimple real algebraic groups. The definition of "tempered representation" makes sense for arbitrary unimodular locally compact group
Locally compact group
In mathematics, a locally compact group is a topological group G which is locally compact as a topological space. Locally compact groups are important because they have a natural measure called the Haar measure. This allows one to define integrals of functions on G.Many of the results of finite...
s, but on groups with infinite centers such as infinite central extensions of semisimple Lie groups it does not behave well and is usually replaced by a slightly different definition.
Tempered representations on semisimple Lie groups were first defined and studied by Harish-Chandra
Harish-Chandra
Harish-Chandra was an Indian mathematician, who did fundamental work in representation theory, especially Harmonic analysis on semisimple Lie groups. -Life:...
(using a different but equivalent definition), who showed that they are exactly the representations needed for the Plancherel theorem
Plancherel theorem
In mathematics, the Plancherel theorem is a result in harmonic analysis, proved by Michel Plancherel in 1910. It states that the integral of a function's squared modulus is equal to the integral of the squared modulus of its frequency spectrum....
. They were classified by Knapp and Zuckerman, and used by Langlands in the Langlands classification
Langlands classification
In mathematics, the Langlands classification is a classification of irreducible representations of a reductive Lie group G, suggested by Robert Langlands...
of irreducible representations of a reductive Lie group G in terms of the tempered representations of smaller groups.
History
Irreducible tempered representations were identified by Harish-ChandraHarish-Chandra
Harish-Chandra was an Indian mathematician, who did fundamental work in representation theory, especially Harmonic analysis on semisimple Lie groups. -Life:...
in his work on harmonic analysis on a semisimple Lie group as those representations that contribute to the Plancherel measure
Plancherel measure
In mathematics, Plancherel measure is a probability measure defined on the set of irreducible representations of a finite group G. In some cases the term Plancherel measure is applied specifically in the context of the group G being the finite symmetric group S_n – see below...
. The original definition of a tempered representation, which has certain technical advantages, is that its Harish-Chandra character
Harish-Chandra character
In mathematics, the Harish-Chandra character, named after Harish-Chandra, of a representation of a semisimple Lie group G on a Hilbert space H is a distribution on the group G that is analogous to the character of a finite dimensional representation of a compact group.-Definition:Suppose that π...
should be a "tempered distribution" (see the section about this below). It follows from Harish-Chandra's results that it is equivalent to the more elementary definition given above. Tempered representations also seem to play a fundamental role in the theory of automorphic form
Automorphic form
In mathematics, the general notion of automorphic form is the extension to analytic functions, perhaps of several complex variables, of the theory of modular forms...
s. This connection was probably first realized by Satake (in the context of the Ramanujan-Petersson conjecture) and Robert Langlands
Robert Langlands
Robert Phelan Langlands is a mathematician, best known as the founder of the Langlands program. He is an emeritus professor at the Institute for Advanced Study...
and served as a motivation for Langlands to develop his classification scheme
Langlands classification
In mathematics, the Langlands classification is a classification of irreducible representations of a reductive Lie group G, suggested by Robert Langlands...
for irreducible admissible representations of real and p-adic reductive algebraic groups in terms of the tempered representations of smaller groups. The precise conjectures identifying the place of tempered representations in the automorphic spectrum were formulated later by James Arthur
James Arthur (mathematician)
James Greig Arthur , is a Canadian mathematician and former President of the American Mathematical Society. He is currently in the Mathematics Departmentof the University of Toronto....
and constitute one of the most actively developing parts of the modern theory of automorphic forms.
Harmonic analysis
Tempered representations play an important role in the harmonic analysis on semisimple Lie groups. An irreducible unitaryUnitary representation
In mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
representation of a semisimple Lie group G is tempered if and only if it is in the support of the Plancherel measure
Plancherel measure
In mathematics, Plancherel measure is a probability measure defined on the set of irreducible representations of a finite group G. In some cases the term Plancherel measure is applied specifically in the context of the group G being the finite symmetric group S_n – see below...
of G. In other words, tempered representations are precisely the class of representations of G appearing in the spectral decomposition of L2 functions on the group (while discrete series representations have a stronger property that an individual representation has a positive spectral measure). This stands in contrast with the situation for abelian and more general solvable Lie groups, where a different class of representations is needed to fully account for the spectral decomposition. This can be seen already in the simplest example of the additive group R of the real numbers, for which the matrix elements of the irreducible representations do not fall off to 0 at infinity.
In the Langlands program
Langlands program
The Langlands program is a web of far-reaching and influential conjectures that relate Galois groups in algebraic number theory to automorphic forms and representation theory of algebraic groups over local fields and adeles. It was proposed by ....
, tempered representations of real Lie groups are those coming from unitary characters of tori by Langlands functoriality.
Examples
- The Plancherel theoremPlancherel theoremIn mathematics, the Plancherel theorem is a result in harmonic analysis, proved by Michel Plancherel in 1910. It states that the integral of a function's squared modulus is equal to the integral of the squared modulus of its frequency spectrum....
for a semisimple Lie group involves representations that are not the discrete series. This becomes clear already in the case of the group SL2(R). The principal series representationPrincipal series representationIn mathematics, the principal series representations of certain kinds of topological group G occur in the case where G is not a compact group. There, by analogy with spectral theory, one expects that the regular representation of G will decompose according to some kind of continuous spectrum, of...
s of SL2(R) are tempered and account for the spectral decomposition of functions supported on the hyperbolic elements of the group. However, they do not occur discretely in the regular representation of SL2(R). - The two limit of discrete series representations of SL2(R) are tempered but not discrete series (even though they occur "discretely" in the list of irreducible unitary representations).
- For non-semisimple Lie groups, representations with matrix coefficients in L2+ε do not always suffice for the Plancherel theoremPlancherel theoremIn mathematics, the Plancherel theorem is a result in harmonic analysis, proved by Michel Plancherel in 1910. It states that the integral of a function's squared modulus is equal to the integral of the squared modulus of its frequency spectrum....
, as shown by the example of the additive group R of real numbers and the Fourier integral; in fact, all irreducible unitary representations of R contribute to the Plancherel measure, but none of them have matrix coefficients in L2+ε. - The complementary series representationComplementary series representationIn mathematics, complementary series representations of a reductive real or p-adic Lie groups are certain irreducible unitary representations that are not tempered and do not appear in the decomposition of the regular representation into irreducible representations.They are rather mysterious: they...
s of SL2(R) are irreducible unitary representations that are not tempered. - The trivial representationTrivial representationIn the mathematical field of representation theory, a trivial representation is a representation of a group G on which all elements of G act as the identity mapping of V...
of a group G is an irreducible unitary representation that is not tempered unless G is compactCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
.
Classification
The irreducible tempered representations of a semisimple Lie group were classified by .In fact they classified a more general class of representations called basic representations. If P=MAN is the Langlands decomposition
Langlands decomposition
In mathematics, the Langlands decomposition writes a parabolic subgroup P of a semisimple Lie group as a product P=MAN of a reductive subgroup M, an abelian subgroup A, and a nilpotent subgroup N.- Applications :...
of a cuspidal parabolic subgroup, then a basic representation is defined to be
the parabolically induced representation associated to a limit of discrete series representation of M and a unitary representation of the abelian group A. If the limit of discrete series representation is in fact a discrete series representation, then the basic representation is called an induced discrete series representation. Any irreducible tempered representation is a basic representation, and conversely any basic representation is the sum of a finite number of irreducible tempered representations. More precisely, it is a direct sum of 2r irreducible tempered representations indexed by the characters of an elementary abelian group R of order 2r (called the R-group).
Any basic representation, and consequently any irreducible tempered representation, is a summand of an induced discrete series representation. However it is not always possible to represent an irreducible tempered representation as an induced discrete series representation, which is why one considers the more general class of basic representations.
So the irreducible tempered representations are just the irreducible basic representations, and can be classified by listing all basic representations and picking out those that are irreducible, in other words those that have trivial R-group.
Tempered distributions
Fix a semisimple Lie group G with maximal compact subgroup K. defined a distribution on G to be tempered if it is defined on the Schwartz space of G. The Schwartz space is in turn defined to be the space of smooth functions f on G such that for any real r and any function g obtained from f by acting on the left or right by elements of the universal enveloping algebra of the Lie algebra of G, the function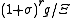
is bounded.
Here Ξ is a certain spherical function on G, invariant under left and right multiplication by K,
and σ is the norm of the log of p, where an element g of G is written as : g=kp
for k in K and p in P.

