Gelfand pair
Encyclopedia
In mathematics
, the expression Gelfand pair is a pair (G, K) consisting of a group
G and a subgroup
K that satisfies a certain property on restricted representation
s. The theory of Gelfand pairs is closely related to the topic of spherical function
s in the classical theory of special functions, and to the theory of Riemannian symmetric space
s in differential geometry. Broadly speaking, the theory exists to abstract from these theories their content in terms of harmonic analysis
and representation theory
.
When G is a finite group the simplest definition is, roughly speaking, that the (K,K)-double cosets in G commute. More precisely, the Hecke algebra, the algebra of functions on G that are invariant under translation on either side by K, should be commutative for the convolution
on G.
In general, the definition of Gelfand pair is roughly that the restriction to H of any irreducible representation of G contains the trivial representation
of H with multiplicity no more than 1. In each case one should specify the class of considered representations and the meaning of contains.
the following are equivalent
and K is a compact subgroup the following are equivalent:
For a classification of such Gelfand pairs see
Classical examples of such Gelfand pairs are (G, K), where G is a reductive Lie group and K is a maximal compact subgroup
.
and K is a compact subgroup the following are equivalent:
and K is a closed subgroup, the pair (G,K) is called a generalized Gelfand pair if for any irreducible unitary representation
π of G on a Hilbert space
we have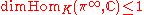
, where 
denotes the subrepresentation of smooth vectors.
over a local field
and K is a closed subgroup, there are three (possibly non-equivalent) notions of Gelfand pair appearing in the literature. We will call them here GP1, GP2, and GP3.
GP1) For any irreducible admissible representation π of G we have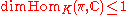
GP2) For any irreducible admissible representation π of G we have
, where 
denotes the smooth dual
.
GP3) For any irreducible unitary representation
π of G on a Hilbert space
we have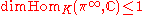
Here, admissible representation is the usual notion of admissible representation
when the local field is non-archimedean. When the local field is archimedean, admissible representation instead means smooth Fréchet
representation
of moderate growth such that the corresponding Harish-Chandra module is admissible.
If the local field is archimedean, then GP3 is the same as generalized Gelfand property defined in the previous case.
Clearly, GP1 ⇒ GP2 ⇒ GP3.
In each of the above cases can be adapted to strong Gelfand pairs. For example, let G be a finite group. Then the following are equivalent.
for the pair (G,K) to be Gelfand: Suppose that there exists an involutive anti-automorphism σ of G s.t. any (K,K) double coset is σ invariant. Then the pair (G,K) is a Gelfand pair.
This criterion is equivalent to the following one: Suppose that there exists an involutive anti-automorphism σ of G such that any function on G which is invariant with respect to both right and left translations by K is σ invariant. Then the pair (G,K) is a Gelfand pair.
and Kazhdan
for the pair (G,K) to satisfy GP2. Suppose that there exists an involutive anti
-automorphism
σ of G such that any (K,K)-double invariant distribution
on G is σ-invariant. Then the pair (G,K) satisfies GP2. See and
If the above statement holds only for positive definite
distributions then the pair satisfies GP3 (see the next case).
The property GP1 often follows from GP2. For example this holds if there exists an involutive anti
-automorphism
of G that preserves K and preserves every closed conjugacy class. For G = GLn the transposition can serve as such involution.
-automorphism
σ of G s.t. any K × K invariant positive definite distribution
on G is σ-invariant. Then the pair (G,K) is a generalized Gelfand pair. See.
of a the grope K, if the Gelfand property holds true when the trivial representation is replaced with the character 
. For example in case when K is compact it meanes that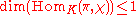 
. One can adapt the criterion for Gelfand pairs to the case of twisted Gelfand pairs
A pair (G,K) is called a symmetric pair if there exists an involutive automorphism
θ of G such that K is a union of connected components of the group of θ-invariant elements Gθ.
If G is a connected
reductive group
over
and 
is a compact subgroup
then (G,K) is a Gelfand pair. Example: G = GLn(R) and K = On(R), the subgroup of orthogonal matrices.
In general, it is an interesting question when a symmetric pair of a reductive group over a local field
has the Gelfand property. For symmetric pairs of rank one this question was investigated in and
An example of high rank Gelfand symmetric pair is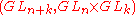
. This was proven in over non-archimedean local fields and later in for all local fields of characteristic
zero.
For more details on this question for high rank symmetric pairs see.
Let (G, K) be a Gelfand pair. An irreducible representation of G called K-distinguished if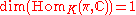
. The representation 
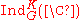is a model for all K-distinguished representations i.e. any K-distinguished representation appears there with multiplicity exactly 1. A similar notion exists for twisted Gelfand pairs.
Examples:
If G is a reductive group over a local field and K is its maximal compact subgroup, then K distinguished representations are called spherical, such representations can be classified via the Satake correspondence. The notion of spherical representation is in the basis of the notion of Harish-Chandra module
.
If G is split reductive group over a local field and K is its maximal unipotent subgroup then the pair (G, K) is twisted Gelfand pair w.r.t. any non-degenerate character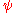
(see,). In this case K-distinguished representations are called generic (or non-degenerate) and they are easy to classify. Almost any irreducible representation is generic. The unique (up to scalar) imbedding of a generic representation to 
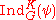is called a Whittaker model
.
In case G = GL(n) there is a finer version of the result above, namely there exist a finite sequence of subgroups K i and characters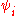
s.t. (G, K i) is twisted Gelfand pair w.r.t. 
and any irreducible unitary representation is K i distinguished for exactly one i (see,
)
Suppose that we have a sequence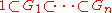
s.t. 
is a strong Gelfand pair. For simplicity let's assume that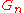 
is compact. Then this gives a canonical decomposition of any irreducible representation of 
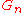to one dimensional subrepresentations. For the case 
(the unitary group) this construction is called Gelfand Zeitlin basis. Note that representations of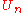 
are the same as algebraic representations of 
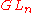so we also obtain a basis of any algebraic irreducible representation of 
.
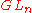Remark: this basis isn't canonical as it depends of the choice of the embeddings
Let G be a reductive group defined over a global field
F and let K be an algebraic subgroup of G. Suppose that for any place
of F the pair (G, K) is a Gelfand pair over the completion
. Let m be an automorphic form
over G, then its H-period splits as a product of local factors (i.e. factors that depends only on the behavior of m at each place
).
Now suppose we are given a family of automorphic forms with a complex parameter s. Then the period of those forms is an analytic function which splits into a product of local factors. Often this means that this function is a certain L-function
and this gives an analytic continuation
and functional equation
for this L-function.
Remark: usually those periods do not converge and one should regularize them.
on the group G w.r.t. the two sided action of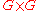
. Indeed, to know all the irreducible representations of G is equivalent to know the decomposition of the space of functions on G as a 
representation. In this approach representation theory can be generalized by replacing the pair 
by any spherical pair (G, K). Then we will be lead to the question of harmonic analysis on the space G/K w.r.t. the action of G.
Now the Gelfand property for the pair (G, K) is an analog of the Schur's lemma
.
Using this approach one can take any concepts of representation theory and generalize them to the case of spherical pair. For example the relative trace formula is obtained from the trace formula
by this procedure.
If (G, K) is a Gelfand pair, then (G/N, K/N) is a Gelfand pair for every G-normal subgroup
N of K. For many purposes it suffices to consider K without any such non-identity normal subgroups. The action of G on the cosets of K is thus faithful, so one is then looking at permutation groups G with point stabilizers K. To be a Gelfand pair is equivalent to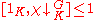
for every χ in Irr(G). Since 
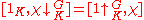by Frobenius reciprocity and 
is the character of the permutation action, a permutation group defines a Gelfand pair if and only if the permutation character is a so-called multiplicity-free permutation character. Such multiplicity-free permutation characters were determined for the sporadic group
s in .
This gives rise to a class of examples of finite groups with Gelfand pairs: the 2-transitive group
s. A permutation group
G is 2-transitive if the stabilizer K of a point acts transitively on the remaining points. In particular, G the symmetric group
on n + 1 points and K the symmetric group on n points forms a Gelfand pair for every n ≥ 1. This follows because the character of a 2-transitive permutation action is of the form 1 + χ for some irreducible character χ and the trivial character 1, .
Indeed, if G is a transitive permutation group whose point stabilizer K has at most four orbits (including the trivial orbit containing only the stabilized point), then its Schur ring is commutative and (G, K) is a Gelfand pair, . If G is a primitive group of degree twice a prime with point stabilizer K, then again (G, K) is a Gelfand pair, .
The Gelfand pairs (Sym(n), K) were classified in . Roughly speaking, K must be contained as a subgroup of small index
in one of the following groups unless n is smaller than 18: Sym(n − k) × Sym(k), Sym(n/2) wr Sym(2), Sym(2) wr Sym(n/2) for n even, Sym(n − 5) × AGL(1, 5), Sym(n − 6) × PGL(2, 5), or Sym(n − 9) × PΓL(2, 8). Gelfand pairs for classical groups have been investigated as well.
of characteristic
zero.
of characteristic
zero. Let G be a reductive group
over F. The following are examples of symmetric Gelfand pairs of high rank:
over F with a non-degenerate
quadratic form
.
See and.
Those four examples can be rephrased in terms of Gelfand pairs as follows. The pairs
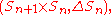
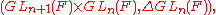
and
are Gelfand pairs.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the expression Gelfand pair is a pair (G, K) consisting of a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
G and a subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
K that satisfies a certain property on restricted representation
Restricted representation
In mathematics, restriction is a fundamental construction in representation theory of groups. Restriction forms a representation of a subgroup from a representation of the whole group. Often the restricted representation is simpler to understand...
s. The theory of Gelfand pairs is closely related to the topic of spherical function
Zonal spherical function
In mathematics, a zonal spherical function or often just spherical function is a function on a locally compact group G with compact subgroup K that arises as the matrix coefficient of a K-invariant vector in an irreducible representation of G...
s in the classical theory of special functions, and to the theory of Riemannian symmetric space
Riemannian symmetric space
In differential geometry, representation theory and harmonic analysis, a symmetric space is a smooth manifold whose group of symmetries contains an inversion symmetry about every point. There are two ways to formulate the inversion symmetry, via Riemannian geometry or via Lie theory...
s in differential geometry. Broadly speaking, the theory exists to abstract from these theories their content in terms of harmonic analysis
Harmonic analysis
Harmonic analysis is the branch of mathematics that studies the representation of functions or signals as the superposition of basic waves. It investigates and generalizes the notions of Fourier series and Fourier transforms...
and representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
.
When G is a finite group the simplest definition is, roughly speaking, that the (K,K)-double cosets in G commute. More precisely, the Hecke algebra, the algebra of functions on G that are invariant under translation on either side by K, should be commutative for the convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
on G.
In general, the definition of Gelfand pair is roughly that the restriction to H of any irreducible representation of G contains the trivial representation
Trivial representation
In the mathematical field of representation theory, a trivial representation is a representation of a group G on which all elements of G act as the identity mapping of V...
of H with multiplicity no more than 1. In each case one should specify the class of considered representations and the meaning of contains.
Definitions
In each area, the class of representations and the definition of containment for representations is slightly different. Explicit definitions in several such cases are given here.Finite group case
When G is a finite groupFinite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
the following are equivalent
- (G,K) is a Gelfand pair.
- The algebra of (K,K)-double invariant functions on G with multiplication defined by convolution is commutative.
- For any irreducible representation π of G, the space πK of K-invariantInvariant (mathematics)In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
vectors in π is no more than 1 dimensional. - For any irreducible representation π of G, we have
, where 
denotes the trivial representationTrivial representationIn the mathematical field of representation theory, a trivial representation is a representation of a group G on which all elements of G act as the identity mapping of V...
. - The permutation representation of G on the cosets of K is multiplicity-free, that is, it decomposes into a direct sum of distinct absolutely irreducibleAbsolutely irreducibleIn mathematics, absolutely irreducible is a term applied to linear representations or algebraic varieties over a field. It means that the object in question remains irreducible, even after any finite extension of the field of coefficients...
representations in characteristicCharacteristic (algebra)In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
zero. - The centralizer algebra (Schur algebraSchur algebraIn mathematics, Schur algebras, named after Issai Schur, are certain finite-dimensional algebras closely associated with Schur–Weyl duality between general linear and symmetric groups. They are used to relate the representation theories of those two groups. Their use was promoted by the...
) of the permutation representation is commutativeCommutative ringIn ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
. - (G/N, K/N) is a Gelfand pair, where N is a normal subgroupNormal subgroupIn abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
of G contained in K.
Compact group case
When G is a compact topological group the following are equivalent:- (G,K) is a Gelfand pair.
- The algebra of (K,K)-double invariant compactly supported continuous measuresMeasure (mathematics)In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
on G with multiplication defined by convolution is commutative. - For any continuous, locally convexLocally convex topological vector spaceIn functional analysis and related areas of mathematics, locally convex topological vector spaces or locally convex spaces are examples of topological vector spaces which generalize normed spaces. They can be defined as topological vector spaces whose topology is generated by translations of ...
, irreducible representation π of G, the space πK of K-invariantInvariant (mathematics)In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
vectors in π is no more than 1 dimensional. - For any continuous, locally convex, irreducible representation π of G we have
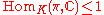. - The representation
of G is multiplicity free i.e. it is a direct sum of distinct unitaryUnitary representationIn mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
irreducible representations.
Lie group with compact subgroup
When G is a Lie groupLie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
and K is a compact subgroup the following are equivalent:
- (G,K) is a Gelfand pair.
- The algebra of (K,K)-double invariant compactly supported continuous measuresMeasure (mathematics)In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
on G with multiplication defined by convolution is commutative. - The algebra D(G/K)K of K-invariant differential operators on G/K is commutative.
- For any continuous, locally convexLocally convex topological vector spaceIn functional analysis and related areas of mathematics, locally convex topological vector spaces or locally convex spaces are examples of topological vector spaces which generalize normed spaces. They can be defined as topological vector spaces whose topology is generated by translations of ...
, irreducible representation π of G, the space πK of K-invariantInvariant (mathematics)In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
vectors in π is no more than 1 dimensional. - For any continuous, locally convex, irreducible representation π of G we have
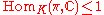. - The representation
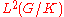of G is multiplicity free i.e. it is a direct integralDirect integralIn mathematics and functional analysis a direct integral is a generalization of the concept of direct sum. The theory is most developed for direct integrals of Hilbert spaces and direct integrals of von Neumann algebras. The concept was introduced in 1949 by John von Neumann in one of the papers...
of distinct unitaryUnitary representationIn mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
irreducible representations.
For a classification of such Gelfand pairs see
Classical examples of such Gelfand pairs are (G, K), where G is a reductive Lie group and K is a maximal compact subgroup
Maximal compact subgroup
In mathematics, a maximal compact subgroup K of a topological group G is a subgroup K that is a compact space, in the subspace topology, and maximal amongst such subgroups....
.
Locally compact topological group with compact subgroup
When G is a locally compact topological groupTopological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
and K is a compact subgroup the following are equivalent:
- (G,K) is a Gelfand pair.
- The algebra of (K, K)-double invariant compactly supported continuous measuresMeasure (mathematics)In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
on G with multiplication defined by convolution is commutative. - For any continuous locally convexLocally convex topological vector spaceIn functional analysis and related areas of mathematics, locally convex topological vector spaces or locally convex spaces are examples of topological vector spaces which generalize normed spaces. They can be defined as topological vector spaces whose topology is generated by translations of ...
irreducible representation π of G, the space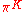
of K-invariantInvariant (mathematics)In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
vectors in π is no more than 1 dimensional. - For any continuous, locally convex, irreducible representation π of G, we have
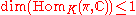. - The representation
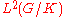of G is multiplicity free i.e. it is a direct integralDirect integralIn mathematics and functional analysis a direct integral is a generalization of the concept of direct sum. The theory is most developed for direct integrals of Hilbert spaces and direct integrals of von Neumann algebras. The concept was introduced in 1949 by John von Neumann in one of the papers...
of distinct unitaryUnitary representationIn mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
irreducible representations.
Lie group with closed subgroup
When G is a Lie groupLie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
and K is a closed subgroup, the pair (G,K) is called a generalized Gelfand pair if for any irreducible unitary representation
Unitary representation
In mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
π of G on a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
we have
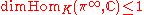, where denotes the subrepresentation of smooth vectors.Reductive group over a local field with closed subgroup
When G is a reductive groupReductive group
In mathematics, a reductive group is an algebraic group G over an algebraically closed field such that the unipotent radical of G is trivial . Any semisimple algebraic group is reductive, as is any algebraic torus and any general linear group...
over a local field
Local field
In mathematics, a local field is a special type of field that is a locally compact topological field with respect to a non-discrete topology.Given such a field, an absolute value can be defined on it. There are two basic types of local field: those in which the absolute value is archimedean and...
and K is a closed subgroup, there are three (possibly non-equivalent) notions of Gelfand pair appearing in the literature. We will call them here GP1, GP2, and GP3.
GP1) For any irreducible admissible representation π of G we have
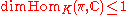
GP2) For any irreducible admissible representation π of G we have
, where denotes the smooth dualDual representation
In mathematics, if G is a group and ρ is a linear representation of it on the vector space V, then the dual representation is defined over the dual vector space as follows:...
.
GP3) For any irreducible unitary representation
Unitary representation
In mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
π of G on a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
we have
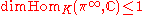
Here, admissible representation is the usual notion of admissible representation
Admissible representation
In mathematics, admissible representations are a well-behaved class of representations used in the representation theory of reductive Lie groups and locally compact totally disconnected groups. They were introduced by Harish-Chandra....
when the local field is non-archimedean. When the local field is archimedean, admissible representation instead means smooth Fréchet
Fréchet space
In functional analysis and related areas of mathematics, Fréchet spaces, named after Maurice Fréchet, are special topological vector spaces. They are generalizations of Banach spaces...
representation
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
of moderate growth such that the corresponding Harish-Chandra module is admissible.
If the local field is archimedean, then GP3 is the same as generalized Gelfand property defined in the previous case.
Clearly, GP1 ⇒ GP2 ⇒ GP3.
Strong Gelfand pairs
A pair (G,K) is called a strong Gelfand pair if the pair (G × K, Δ K) is a Gelfand pair, where ΔK ≤ G × K is the diagonal subgroup, ΔK = { ( k, k ) in G × K : k in K }. Sometimes, this property is also called the multiplicity one property.In each of the above cases can be adapted to strong Gelfand pairs. For example, let G be a finite group. Then the following are equivalent.
- (G,K) is a strong Gelfand pair.
- The algebra of functions on G invariant with respect to conjugation by K (with multiplication defined by convolution) is commutative.
- For any irreducible representation π of G and τ of K, the space
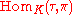is no more than 1-dimensional. - For any irreducible representation π of G and τ of K, the space
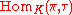is no more than 1-dimensional.
Locally compact topological group with compact subgroup
In this case there is a classical criterion due to GelfandIsrael Gelfand
Israel Moiseevich Gelfand, also written Israïl Moyseyovich Gel'fand, or Izrail M. Gelfand was a Soviet mathematician who made major contributions to many branches of mathematics, including group theory, representation theory and functional analysis...
for the pair (G,K) to be Gelfand: Suppose that there exists an involutive anti-automorphism σ of G s.t. any (K,K) double coset is σ invariant. Then the pair (G,K) is a Gelfand pair.
This criterion is equivalent to the following one: Suppose that there exists an involutive anti-automorphism σ of G such that any function on G which is invariant with respect to both right and left translations by K is σ invariant. Then the pair (G,K) is a Gelfand pair.
Reductive group over a local field with closed subgroup
In this case there is a criterion due to GelfandIsrael Gelfand
Israel Moiseevich Gelfand, also written Israïl Moyseyovich Gel'fand, or Izrail M. Gelfand was a Soviet mathematician who made major contributions to many branches of mathematics, including group theory, representation theory and functional analysis...
and Kazhdan
David Kazhdan
David Kazhdan or Každan, Kazhdan, formerly named Dmitry Aleksandrovich Kazhdan , is a Soviet and Israeli mathematician known for work in representation theory.-Life:...
for the pair (G,K) to satisfy GP2. Suppose that there exists an involutive anti
Antihomomorphism
In mathematics, an antihomomorphism is a type of function defined on sets with multiplication that reverses the order of multiplication. An antiautomorphism is an antihomomorphism which has an inverse as an antihomomorphism; this coincides with it being a bijection from an object to...
-automorphism
Automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
σ of G such that any (K,K)-double invariant distribution
Distribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
on G is σ-invariant. Then the pair (G,K) satisfies GP2. See and
If the above statement holds only for positive definite
Positive definite function on a group
In operator theory, a positive-definite function on a group relates the notions of positivity, in the context of Hilbert spaces, and algebraic groups...
distributions then the pair satisfies GP3 (see the next case).
The property GP1 often follows from GP2. For example this holds if there exists an involutive anti
Antihomomorphism
In mathematics, an antihomomorphism is a type of function defined on sets with multiplication that reverses the order of multiplication. An antiautomorphism is an antihomomorphism which has an inverse as an antihomomorphism; this coincides with it being a bijection from an object to...
-automorphism
Automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
of G that preserves K and preserves every closed conjugacy class. For G = GLn the transposition can serve as such involution.
Lie group with closed subgroup
In this case there is the following criterion for the pair (G,K) to be generalized Gelfand pair. Suppose that there exists an involutive antiAntihomomorphism
In mathematics, an antihomomorphism is a type of function defined on sets with multiplication that reverses the order of multiplication. An antiautomorphism is an antihomomorphism which has an inverse as an antihomomorphism; this coincides with it being a bijection from an object to...
-automorphism
Automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
σ of G s.t. any K × K invariant positive definite distribution
Distribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
on G is σ-invariant. Then the pair (G,K) is a generalized Gelfand pair. See.
Criteria for strong Gelfand property
All the above criteria can be turned into criteria for strong Gelfand pairs by replacing the two-sided action of K × K by the conjugation action of K.Twisted Gelfand pairs
A generalization of the notion of Gelfand pair is the notion of twisted Gelfand pair. Namely a pair (G, K) is called a twisted Gelfand pair with respect to the character of a the grope K, if the Gelfand property holds true when the trivial representation is replaced with the character . For example in case when K is compact it meanes that 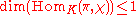. One can adapt the criterion for Gelfand pairs to the case of twisted Gelfand pairsSymmetric pairs
The Gelfand property is often satisfied by symmetric pairs.A pair (G,K) is called a symmetric pair if there exists an involutive automorphism
Automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
θ of G such that K is a union of connected components of the group of θ-invariant elements Gθ.
If G is a connected
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
reductive group
Reductive group
In mathematics, a reductive group is an algebraic group G over an algebraically closed field such that the unipotent radical of G is trivial . Any semisimple algebraic group is reductive, as is any algebraic torus and any general linear group...
over
and is a compact subgroupSubgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
then (G,K) is a Gelfand pair. Example: G = GLn(R) and K = On(R), the subgroup of orthogonal matrices.
In general, it is an interesting question when a symmetric pair of a reductive group over a local field
Local field
In mathematics, a local field is a special type of field that is a locally compact topological field with respect to a non-discrete topology.Given such a field, an absolute value can be defined on it. There are two basic types of local field: those in which the absolute value is archimedean and...
has the Gelfand property. For symmetric pairs of rank one this question was investigated in and
An example of high rank Gelfand symmetric pair is
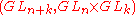. This was proven in over non-archimedean local fields and later in for all local fields of characteristicCharacteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
zero.
For more details on this question for high rank symmetric pairs see.
Spherical pairs
If G is a reductive group over a local field there is another property that is weaker than the Gelfand property, but is easier to verify. Namely, the pair (G,K) is called a spherical pair if one the following equivalent conditions holds.- For any parabolic subgroup P of G there exists an open (P,K)-double coset in G.
- For any parabolic subgroup P of G there is a finite number of (P,K)-double cosets in G.
- For any admissible representation π of G, the space
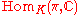is finite dimensional.
Classification
Gelfand pairs are often used for classification of irreducible representations in the following way:Let (G, K) be a Gelfand pair. An irreducible representation of G called K-distinguished if
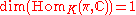. The representation 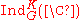is a model for all K-distinguished representations i.e. any K-distinguished representation appears there with multiplicity exactly 1. A similar notion exists for twisted Gelfand pairs.Examples:
If G is a reductive group over a local field and K is its maximal compact subgroup, then K distinguished representations are called spherical, such representations can be classified via the Satake correspondence. The notion of spherical representation is in the basis of the notion of Harish-Chandra module
Harish-Chandra module
In mathematics, specifically in the representation theory of Lie groups, a Harish-Chandra module is a representation of a real Lie group, associated to a general representation, with regularity and finiteness conditions...
.
If G is split reductive group over a local field and K is its maximal unipotent subgroup then the pair (G, K) is twisted Gelfand pair w.r.t. any non-degenerate character
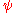(see,). In this case K-distinguished representations are called generic (or non-degenerate) and they are easy to classify. Almost any irreducible representation is generic. The unique (up to scalar) imbedding of a generic representation to 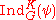is called a Whittaker modelWhittaker model
In representation theory, a branch of mathematics, the Whittaker model is a realization of a representation of a reductive algebraic group such as GL2 over a finite or local or global field on a space of functions on the group. It is named after E. T...
.
In case G = GL(n) there is a finer version of the result above, namely there exist a finite sequence of subgroups K i and characters
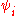s.t. (G, K i) is twisted Gelfand pair w.r.t. and any irreducible unitary representation is K i distinguished for exactly one i (see,)
Gelfand–Zeitlin construction
Another use of Gelfand pairs is for construction of bases of irreducible representations.Suppose that we have a sequence
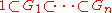s.t. is a strong Gelfand pair. For simplicity let's assume that 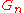is compact. Then this gives a canonical decomposition of any irreducible representation of 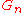to one dimensional subrepresentations. For the case (the unitary group) this construction is called Gelfand Zeitlin basis. Note that representations of 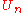are the same as algebraic representations of 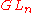so we also obtain a basis of any algebraic irreducible representation of 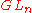.Remark: this basis isn't canonical as it depends of the choice of the embeddings
Splitting of periods of automorphic forms
A more recent use of Gelfand pairs is for splitting of periods of automorphic forms.Let G be a reductive group defined over a global field
Global field
In mathematics, the term global field refers to either of the following:*an algebraic number field, i.e., a finite extension of Q, or*a global function field, i.e., the function field of an algebraic curve over a finite field, equivalently, a finite extension of Fq, the field of rational functions...
F and let K be an algebraic subgroup of G. Suppose that for any place
of F the pair (G, K) is a Gelfand pair over the completionCompletion (ring theory)
In abstract algebra, a completion is any of several related functors on rings and modules that result in complete topological rings and modules. Completion is similar to localization, and together they are among the most basic tools in analysing commutative rings. Complete commutative rings have...
. Let m be an automorphic formAutomorphic form
In mathematics, the general notion of automorphic form is the extension to analytic functions, perhaps of several complex variables, of the theory of modular forms...
over G, then its H-period splits as a product of local factors (i.e. factors that depends only on the behavior of m at each place
).Now suppose we are given a family of automorphic forms with a complex parameter s. Then the period of those forms is an analytic function which splits into a product of local factors. Often this means that this function is a certain L-function
L-function
The theory of L-functions has become a very substantial, and still largely conjectural, part of contemporary analytic number theory. In it, broad generalisations of the Riemann zeta function and the L-series for a Dirichlet character are constructed, and their general properties, in most cases...
and this gives an analytic continuation
Analytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
and functional equation
Functional equation
In mathematics, a functional equation is any equation that specifies a function in implicit form.Often, the equation relates the value of a function at some point with its values at other points. For instance, properties of functions can be determined by considering the types of functional...
for this L-function.
Remark: usually those periods do not converge and one should regularize them.
Generalization of representation theory
A possible approach to representation theory is to consider representation theory of a group G as a harmonic analysisHarmonic analysis
Harmonic analysis is the branch of mathematics that studies the representation of functions or signals as the superposition of basic waves. It investigates and generalizes the notions of Fourier series and Fourier transforms...
on the group G w.r.t. the two sided action of
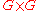. Indeed, to know all the irreducible representations of G is equivalent to know the decomposition of the space of functions on G as a representation. In this approach representation theory can be generalized by replacing the pair by any spherical pair (G, K). Then we will be lead to the question of harmonic analysis on the space G/K w.r.t. the action of G.Now the Gelfand property for the pair (G, K) is an analog of the Schur's lemma
Schur's lemma
In mathematics, Schur's lemma is an elementary but extremely useful statement in representation theory of groups and algebras. In the group case it says that if M and N are two finite-dimensional irreducible representations...
.
Using this approach one can take any concepts of representation theory and generalize them to the case of spherical pair. For example the relative trace formula is obtained from the trace formula
Trace formula
*Arthur–Selberg trace formula*Invariant trace formula*Jacquet's relative trace formula*Kuznetsov trace formula*Local trace formula*Petersson trace formula*Selberg trace formula*Simple trace formula*Stable trace formula...
by this procedure.
Finite groups
A few common examples of Gelfand pairs are:- (Sym(n + 1), Sym(n)), the symmetric groupSymmetric groupIn mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
acting on n+1 points and a point stabilizer that is naturally isomorphic to on n points. - (AGL(n, q), GL(n, q)), the affine (general linear) groupAffine groupIn mathematics, the affine group or general affine group of any affine space over a field K is the group of all invertible affine transformations from the space into itself.It is a Lie group if K is the real or complex field or quaternions....
and a point stabilizer that is naturally isomorphic to the general linear groupGeneral linear groupIn mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
.
If (G, K) is a Gelfand pair, then (G/N, K/N) is a Gelfand pair for every G-normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
N of K. For many purposes it suffices to consider K without any such non-identity normal subgroups. The action of G on the cosets of K is thus faithful, so one is then looking at permutation groups G with point stabilizers K. To be a Gelfand pair is equivalent to
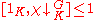for every χ in Irr(G). Since 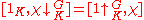by Frobenius reciprocity and is the character of the permutation action, a permutation group defines a Gelfand pair if and only if the permutation character is a so-called multiplicity-free permutation character. Such multiplicity-free permutation characters were determined for the sporadic groupSporadic group
In the mathematical field of group theory, a sporadic group is one of the 26 exceptional groups in the classification of finite simple groups. A simple group is a group G that does not have any normal subgroups except for the subgroup consisting only of the identity element, and G itself...
s in .
This gives rise to a class of examples of finite groups with Gelfand pairs: the 2-transitive group
2-transitive group
In the area of abstract algebra known as group theory, a 2-transitive group is a transitive permutation group in which a point stabilizer acts transitively on the remaining points. Every 2-transitive group is a primitive group, but not conversely. Every Zassenhaus group is 2-transitive, but not...
s. A permutation group
Permutation group
In mathematics, a permutation group is a group G whose elements are permutations of a given set M, and whose group operation is the composition of permutations in G ; the relationship is often written as...
G is 2-transitive if the stabilizer K of a point acts transitively on the remaining points. In particular, G the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
on n + 1 points and K the symmetric group on n points forms a Gelfand pair for every n ≥ 1. This follows because the character of a 2-transitive permutation action is of the form 1 + χ for some irreducible character χ and the trivial character 1, .
Indeed, if G is a transitive permutation group whose point stabilizer K has at most four orbits (including the trivial orbit containing only the stabilized point), then its Schur ring is commutative and (G, K) is a Gelfand pair, . If G is a primitive group of degree twice a prime with point stabilizer K, then again (G, K) is a Gelfand pair, .
The Gelfand pairs (Sym(n), K) were classified in . Roughly speaking, K must be contained as a subgroup of small index
Index of a subgroup
In mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
in one of the following groups unless n is smaller than 18: Sym(n − k) × Sym(k), Sym(n/2) wr Sym(2), Sym(2) wr Sym(n/2) for n even, Sym(n − 5) × AGL(1, 5), Sym(n − 6) × PGL(2, 5), or Sym(n − 9) × PΓL(2, 8). Gelfand pairs for classical groups have been investigated as well.
Symmetric pairs with compact K
-
-
-
-
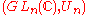
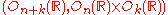
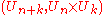
- (G,K) where G is a reductive Lie group and K is a maximal compact subgroupMaximal compact subgroupIn mathematics, a maximal compact subgroup K of a topological group G is a subgroup K that is a compact space, in the subspace topology, and maximal amongst such subgroups....
.
Symmetric Gelfand pairs of rank one
Let F be a local fieldLocal field
In mathematics, a local field is a special type of field that is a locally compact topological field with respect to a non-discrete topology.Given such a field, an absolute value can be defined on it. There are two basic types of local field: those in which the absolute value is archimedean and...
of characteristic
Characteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
zero.
-
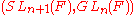for 
-
-
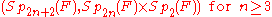
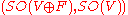where V is a vector space over F with a non-degenerateDegenerate formIn mathematics, specifically linear algebra, a degenerate bilinear form ƒ on a vector space V is one such that the map from V to V^* given by v \mapsto is not an isomorphism...
quadratic formQuadratic formIn mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
.
Symmetric pairs of high rank
Let F be a local fieldLocal field
In mathematics, a local field is a special type of field that is a locally compact topological field with respect to a non-discrete topology.Given such a field, an absolute value can be defined on it. There are two basic types of local field: those in which the absolute value is archimedean and...
of characteristic
Characteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
zero. Let G be a reductive group
Reductive group
In mathematics, a reductive group is an algebraic group G over an algebraically closed field such that the unipotent radical of G is trivial . Any semisimple algebraic group is reductive, as is any algebraic torus and any general linear group...
over F. The following are examples of symmetric Gelfand pairs of high rank:
-
: Follows from Schur's lemmaSchur's lemmaIn mathematics, Schur's lemma is an elementary but extremely useful statement in representation theory of groups and algebras. In the group case it says that if M and N are two finite-dimensional irreducible representations...
. -
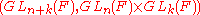: See and. -
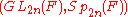: See and. -
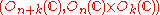: See. -
: See. -
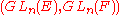, where E is a quadratic extension of F. See and.
Strong Gelfand pairs
The following pairs are strong Gelfand pairs:-
is a strong Gelfand pair, where 
denotes the symmetric groupSymmetric groupIn mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
of n elements. This is proven using the involutive antiAntihomomorphismIn mathematics, an antihomomorphism is a type of function defined on sets with multiplication that reverses the order of multiplication. An antiautomorphism is an antihomomorphism which has an inverse as an antihomomorphism; this coincides with it being a bijection from an object to...
-automorphismAutomorphismIn mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
. -
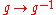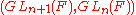where F is a local fieldLocal fieldIn mathematics, a local field is a special type of field that is a locally compact topological field with respect to a non-discrete topology.Given such a field, an absolute value can be defined on it. There are two basic types of local field: those in which the absolute value is archimedean and...
s of characteristicCharacteristic (algebra)In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
zero. See, and. -
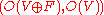where V is a vector space
over F with a non-degenerate
Degenerate form
In mathematics, specifically linear algebra, a degenerate bilinear form ƒ on a vector space V is one such that the map from V to V^* given by v \mapsto is not an isomorphism...
quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
.
See and.
-
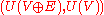where E is a quadratic extension of F and V is a vector space over E with a non-degenerateDegenerate formIn mathematics, specifically linear algebra, a degenerate bilinear form ƒ on a vector space V is one such that the map from V to V^* given by v \mapsto is not an isomorphism...
hermitian form. See and.
Those four examples can be rephrased in terms of Gelfand pairs as follows. The pairs
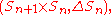
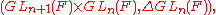
andare Gelfand pairs.
See also
- spherical functionZonal spherical functionIn mathematics, a zonal spherical function or often just spherical function is a function on a locally compact group G with compact subgroup K that arises as the matrix coefficient of a K-invariant vector in an irreducible representation of G...
- Riemannian symmetric spaceRiemannian symmetric spaceIn differential geometry, representation theory and harmonic analysis, a symmetric space is a smooth manifold whose group of symmetries contains an inversion symmetry about every point. There are two ways to formulate the inversion symmetry, via Riemannian geometry or via Lie theory...
- Symmetric pair
- Spherical pair