Positive definite function on a group
Encyclopedia
In operator theory
, a positive-definite function on a group relates the notions of positivity, in the context of Hilbert space
s, and algebraic group
s. It can be viewed as a particular type of positive-definite kernel where the underlying set has the additional group structure.
A positive-definite function on G is a function that satisfies
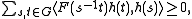
for every function h: G → H with finite support (h takes non-zero values for only finitely many s).
In other words, a function F: G → L(H) is said to be a positive function if the kernel K: G × G → L(H) defined by K(s, t) = F(s−1t) is a positive-definite kernel.
is an unital homomorphism Φ: G → L(H) where Φ(s) is an unitary operator for all s. For such Φ, Φ(s−1) = Φ(s)*.
Positive functions on G is intimately related to unitary representations of G. Every unitary representation of G gives rise to a family of positive-definite functions. Conversely, given a positive-definite function, one can define a unitary representation of G in a natural way.
Let Φ: G → L(H) be a unitary representation of G. If P ∈ L(H) is the projection onto a closed subspace H` of H. Then F(s) = P Φ(s) is a positive-definite function on G with values in L(H`). This can be shown readily:
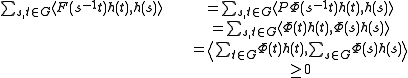
for every h: G → H` with finite support. If G has a topology and Φ is weakly(resp. strongly) continuous, then clearly so is F.
On the other hand, consider now a positive-definite function F on G. An unitary representation of G can be obtained as follows. Let C00(G, H) be the family of functions h: G → H with finite support. The corresponding positive kernel K(s, t) = F(s−1t) defines a (possibly degenerate) inner product on C00(G, H). Let the resulting Hilbert space be denoted by V.
We notice that the "matrix elements" K(s, t) = K(a−1s, a−1t) for all a, s, t in G. So Uah(s) = h(a−1s) preserves the inner product on V, i.e. it is unitary in L(V). It is clear that the map Φ(a) = Ua is a representation of G on V.
The unitary representation is unique, up to Hilbert space isomorphism, provided the following minimality condition holds:
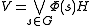
where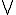
denotes the closure of the linear span.
Identify H as, elements (possibly equivalence classes) in V, whose support consists of the identity element e ∈ G, and let P be the projection onto this subspace. Then we have PUaP = F(a) for all a ∈ G.
. If F is of the form F(n) = Tn where T is a bounded operator acting on some Hilbert space. One can show that the kernel K(n, m) is positive if and only if T is a contraction
. By the discussion from the previous section, we have a unitary representation of Z, Φ(n) = Un for an unitary operator U. Moreover, the property PUaP = F(a) now translates to PUnP = Tn. This is precisely Sz.-Nagy's dilation theorem
and hints at an important dilation-theoretic characterization of positivity that leads to a parametrization of arbitrary positive-definite kernels.
Operator theory
In mathematics, operator theory is the branch of functional analysis that focuses on bounded linear operators, but which includes closed operators and nonlinear operators.Operator theory also includes the study of algebras of operators....
, a positive-definite function on a group relates the notions of positivity, in the context of Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
s, and algebraic group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
s. It can be viewed as a particular type of positive-definite kernel where the underlying set has the additional group structure.
Definition
Let G be a group, H be a complex Hilbert space, and L(H) be the bounded operators on H.A positive-definite function on G is a function that satisfies
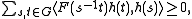
for every function h: G → H with finite support (h takes non-zero values for only finitely many s).
In other words, a function F: G → L(H) is said to be a positive function if the kernel K: G × G → L(H) defined by K(s, t) = F(s−1t) is a positive-definite kernel.
Unitary representations
An unitary representationUnitary representation
In mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
is an unital homomorphism Φ: G → L(H) where Φ(s) is an unitary operator for all s. For such Φ, Φ(s−1) = Φ(s)*.
Positive functions on G is intimately related to unitary representations of G. Every unitary representation of G gives rise to a family of positive-definite functions. Conversely, given a positive-definite function, one can define a unitary representation of G in a natural way.
Let Φ: G → L(H) be a unitary representation of G. If P ∈ L(H) is the projection onto a closed subspace H` of H. Then F(s) = P Φ(s) is a positive-definite function on G with values in L(H`). This can be shown readily:
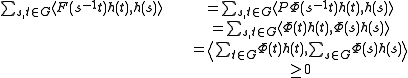
for every h: G → H` with finite support. If G has a topology and Φ is weakly(resp. strongly) continuous, then clearly so is F.
On the other hand, consider now a positive-definite function F on G. An unitary representation of G can be obtained as follows. Let C00(G, H) be the family of functions h: G → H with finite support. The corresponding positive kernel K(s, t) = F(s−1t) defines a (possibly degenerate) inner product on C00(G, H). Let the resulting Hilbert space be denoted by V.
We notice that the "matrix elements" K(s, t) = K(a−1s, a−1t) for all a, s, t in G. So Uah(s) = h(a−1s) preserves the inner product on V, i.e. it is unitary in L(V). It is clear that the map Φ(a) = Ua is a representation of G on V.
The unitary representation is unique, up to Hilbert space isomorphism, provided the following minimality condition holds:
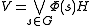
where
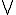denotes the closure of the linear span.Identify H as, elements (possibly equivalence classes) in V, whose support consists of the identity element e ∈ G, and let P be the projection onto this subspace. Then we have PUaP = F(a) for all a ∈ G.
Toeplitz kernels
Let G be the additive group of integers Z. The kernel K(n, m) = F(m − n) is called a kernel of Toeplitz type, by analogy with Toeplitz matricesToeplitz matrix
In linear algebra, a Toeplitz matrix or diagonal-constant matrix, named after Otto Toeplitz, is a matrix in which each descending diagonal from left to right is constant...
. If F is of the form F(n) = Tn where T is a bounded operator acting on some Hilbert space. One can show that the kernel K(n, m) is positive if and only if T is a contraction
Contraction
Contraction may refer to:In physiology:* Muscle contraction, one that occurs when a muscle fiber lengthens or shortens** Uterine contraction, contraction of the uterus, such as during childbirth* Contraction, a stage in wound healing...
. By the discussion from the previous section, we have a unitary representation of Z, Φ(n) = Un for an unitary operator U. Moreover, the property PUaP = F(a) now translates to PUnP = Tn. This is precisely Sz.-Nagy's dilation theorem
Sz.-Nagy's dilation theorem
The Sz.-Nagy dilation theorem states that every contraction T on a Hilbert space H has a unitary dilation U to a Hilbert space K, containing H, withT^n = P_H U^n \vert_H,\quad n\ge 0....
and hints at an important dilation-theoretic characterization of positivity that leads to a parametrization of arbitrary positive-definite kernels.