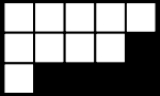
Young tableau
Encyclopedia
In mathematics
, a Young tableau (pl.: tableaux) is a combinatorial
object useful in representation theory
. It provides a convenient way to describe the group representation
s of the symmetric
and general linear
groups and to study their properties. Young tableaux were introduced by Alfred Young
, a mathematician
at Cambridge University
, in 1900. They were then applied to the study of the symmetric group by Georg Frobenius in 1903. Their theory was further developed by many mathematicians, including Percy MacMahon, W. V. D. Hodge
, G. de B. Robinson
, Gian-Carlo Rota
, Alain Lascoux
, Marcel-Paul Schützenberger
and Richard P. Stanley
.
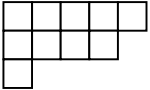
A Young diagram (also called Ferrers diagram, particularly when represented using dots) is a finite collection of boxes, or cells, arranged in left-justified rows, with the row lengths weakly decreasing (each row has the same or shorter length than its predecessor). Listing the number of boxes in each row gives a partition
of a non-negative integer , the total number of boxes of the diagram. The Young diagram is said to be of shape , and it carries the same information as that partition. Containment of one Young diagram in another defines a partial ordering on the set of all partitions, which is in fact a lattice
structure, known as Young's lattice
. Listing the number of boxes of a Young diagram in each column gives another partition, the conjugate or transpose partition of ; one obtains a Young diagram of that shape by reflecting the original diagram along its main diagonal.
There is almost universal agreement that in labeling boxes of Young diagrams by pairs of integers, the first index selects the row of the diagram, and the second index selects the box within the row. Nevertheless two distinct conventions exist to display these diagrams, and consequently tableaux: the first places each row below the previous one, the second stacks each row on top of the previous one. Since the former convention is mainly used by Anglophones
while the latter is often preferred by Francophone
s, it is customary to refer to these conventions respectively as the English notation and the French notation; for instance, in his book on symmetric function
s, Macdonald
advises readers preferring the French convention to "read this book upside down in a mirror" (Macdonald 1979, p.2). This nomenclature probably started out as jocular. The English notation corresponds to the one universally used for matrices, while the French notation is closer to the convention of Cartesian coordinates; however, French notation differs from that convention by placing the vertical coordinate first. The figure on the right shows, using the English notation, the Young diagram corresponding to the partition (5, 4, 1) of the number 10. The conjugate partition, measuring the column lengths, is (3, 2, 2, 2, 1).
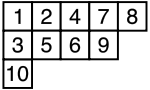A Young tableau is obtained by filling in the boxes of the Young diagram with symbols taken from some alphabet, which is usually required to be a totally ordered set. Originally that alphabet was a set of indexed variables , , ..., but now one usually uses a set of numbers for brevity. In their original application to representations of the symmetric group, Young tableaux have distinct entries, arbitrarily assigned to boxes of the diagram. A tableau is called standard if the entries in each row and each column are increasing.
In other applications, it is natural to allow the same number to appear more than once (or not at all) in a tableau. A tableau is called semistandard, or column strict, if the entries weakly increase along each row and strictly increase down each column. Recording the number of times each number appears in a tableau gives a sequence known as the weight of the tableau. Thus the standard Young tableaux are precisely the semistandard tableaux of weight (1,1,...,1), which requires every integer up to to occur exactly once.
Any skew semistandard tableau of shape / with positive integer entries gives rise to a sequence of partitions (or Young diagrams), by starting with , and taking for the partition places further in the sequence the one whose diagram is obtained from that of by adding all the boxes that contain a value ≤ in ; this partition eventually becomes equal to . Any pair of successive shapes in such a sequence is a skew shape whose diagram contains at most one box in each column; such shapes are called horizontal strips. This sequence of partitions completely determines , and it is in fact possible to define (skew) semistandard tableaux as such sequences, as is done by Macdonald (Macdonald 1979, p.4). Note that this definition incorporates the partitions and in the data comprising the skew tableau.
, representation theory
, and algebraic geometry
. Various ways of counting Young tableaux have been explored and lead to the definition of and identities for Schur functions. Many combinatorial algorithms on tableaux are known, including Schützenberger's jeu de taquin
and the Robinson–Schensted–Knuth correspondence
. Lascoux and Schützenberger studied an associative product on the set of all semistandard Young tableaux, giving it the structure called the plactic monoid (French: le monoïde plaxique).
In representation theory, standard Young tableaux of size describe bases in irreducible representations of the symmetric group
on letters. The standard monomial basis in a finite-dimensional irreducible representation of the general linear group
are parametrized by the set of semistandard Young tableaux of a fixed shape over the alphabet {1, 2, ..., }. This has important consequences for invariant theory
, starting from the work of Hodge
on the homogeneous coordinate ring
of the Grassmanian and further explored by Gian-Carlo Rota
with collaborators, de Concini and Procesi, and Eisenbud
. The Littlewood–Richardson rule
describing (among other things) the decomposition of tensor product
s of irreducible representations of into irreducible components is formulated in terms of certain skew semistandard tableaux.
Applications to algebraic geometry center around Schubert calculus
on Grassmanians and flag varieties. Certain important cohomology classes can be represented by Schubert polynomial
s and described in terms of Young tableaux.
over the complex number
s. They provide a convenient way of specifying the Young symmetrizer
s from which the irreducible representations
are built. Many facts about a representation can be deduced from the corresponding diagram. Below, we describe two examples: determining the dimension of a representation and restricted representations. In both cases, we will see that some properties of a representation can be determined by using just its diagram.
Young diagrams also parametrize the irreducible polynomial representations of the general linear group
(when they have at most nonempty rows), or the irreducible representations of the special linear group
(when they have at most nonempty rows), or the irreducible complex representations of the special unitary group
(again when they have at most nonempty rows). In these case semistandard tableaux with entries up to play a central role, rather than standard tableaux; in particular it is the number of those tableaux that determines the dimension of the representation.
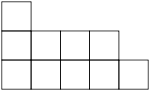
A hook length of a box in Young diagram of shape is the number of boxes that are in the same row to the right of it plus those boxes in the same column below it, plus one (for the box itself). By the hook-length formula, the dimension of an irreducible representation is divided by the product of the hook lengths of all boxes in the diagram of the representation:
The figure on the right shows hook-lengths for all boxes in the diagram of the partition 10 = 5 + 4 + 1. Thus
Similarly, the dimension of the irreducible representation of corresponding to the partition λ of n (with at most r parts) is the number of semistandard Young tableaux of shape λ (containing only the entries from 1 to r), which is given by the hook-length formula:
where the index i gives the row and j the column of a box. For instance, for the partition (5,4,1) we get as dimension of the corresponding irreducible representation of (traversing the boxes by rows):
(see also induced representation
).
The question of determining this decomposition of the restricted representation of a given irreducible representation of Sn, corresponding to a partition of , is answered as follows. One forms the set of all Young diagrams that can be obtained from the diagram of shape by removing just one box (which must be at the end both of its row and of its column); the restricted representation then decomposes as a direct sum of the irreducible representations of corresponding to those diagrams, each occurring exactly once in the sum.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Young tableau (pl.: tableaux) is a combinatorial
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
object useful in representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
. It provides a convenient way to describe the group representation
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
s of the symmetric
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
and general linear
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
groups and to study their properties. Young tableaux were introduced by Alfred Young
Alfred Young
Alfred Young, FRS was a British mathematician.He was born in Widnes, Lancashire, England and educated at Monkton Combe School in Somerset and Clare College, Cambridge, graduating BA as 10th Wrangler in 1895. He is known for his work in the area of group theory...
, a mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
at Cambridge University
University of Cambridge
The University of Cambridge is a public research university located in Cambridge, United Kingdom. It is the second-oldest university in both the United Kingdom and the English-speaking world , and the seventh-oldest globally...
, in 1900. They were then applied to the study of the symmetric group by Georg Frobenius in 1903. Their theory was further developed by many mathematicians, including Percy MacMahon, W. V. D. Hodge
W. V. D. Hodge
William Vallance Douglas Hodge FRS was a Scottish mathematician, specifically a geometer.His discovery of far-reaching topological relations between algebraic geometry and differential geometry—an area now called Hodge theory and pertaining more generally to Kähler manifolds—has been a major...
, G. de B. Robinson
Gilbert de Beauregard Robinson
Gilbert de Beauregard Robinson was a Canadian mathematician most famous for his work on combinatorics and representation theory of the symmetric groups, including the Robinson-Schensted algorithm.-Biography:...
, Gian-Carlo Rota
Gian-Carlo Rota
Gian-Carlo Rota was an Italian-born American mathematician and philosopher.-Life:Rota was born in Vigevano, Italy...
, Alain Lascoux
Alain Lascoux
Alain Lascoux is a French mathematician at the University of Marne la Vallée and Nankai University. His research fields include algebraic combinatorics, particuarly Hecke algebra and Young tableau....
, Marcel-Paul Schützenberger
Marcel-Paul Schützenberger
Marcel-Paul "Marco" Schützenberger was a French mathematician and Doctor of Medicine. His work had impact across the fields of formal language, combinatorics, and information theory...
and Richard P. Stanley
Richard P. Stanley
Richard Peter Stanley is the Norman Levinson Professor of Applied Mathematics at the Massachusetts Institute of Technology, in Cambridge, Massachusetts. He received his Ph.D. at Harvard University in 1971 under the supervision of Gian-Carlo Rota...
.
Definitions
Note: this article uses the English convention for displaying Young diagrams and tableaux.Diagrams
Partition (number theory)
In number theory and combinatorics, a partition of a positive integer n, also called an integer partition, is a way of writing n as a sum of positive integers. Two sums that differ only in the order of their summands are considered to be the same partition; if order matters then the sum becomes a...
of a non-negative integer , the total number of boxes of the diagram. The Young diagram is said to be of shape , and it carries the same information as that partition. Containment of one Young diagram in another defines a partial ordering on the set of all partitions, which is in fact a lattice
Lattice (order)
In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
structure, known as Young's lattice
Young's lattice
In mathematics, Young's lattice is a partially ordered set and a lattice that is formed by all integer partitions. It is named after Alfred Young, who in a series of papers On quantitative substitutional analysis developed representation theory of the symmetric group...
. Listing the number of boxes of a Young diagram in each column gives another partition, the conjugate or transpose partition of ; one obtains a Young diagram of that shape by reflecting the original diagram along its main diagonal.
There is almost universal agreement that in labeling boxes of Young diagrams by pairs of integers, the first index selects the row of the diagram, and the second index selects the box within the row. Nevertheless two distinct conventions exist to display these diagrams, and consequently tableaux: the first places each row below the previous one, the second stacks each row on top of the previous one. Since the former convention is mainly used by Anglophones
English-speaking world
The English-speaking world consists of those countries or regions that use the English language to one degree or another. For more information, please see:Lists:* List of countries by English-speaking population...
while the latter is often preferred by Francophone
Francophone
The adjective francophone means French-speaking, typically as primary language, whether referring to individuals, groups, or places. Often, the word is used as a noun to describe a natively French-speaking person....
s, it is customary to refer to these conventions respectively as the English notation and the French notation; for instance, in his book on symmetric function
Symmetric function
In algebra and in particular in algebraic combinatorics, the ring of symmetric functions, is a specific limit of the rings of symmetric polynomials in n indeterminates, as n goes to infinity...
s, Macdonald
Ian G. Macdonald
Ian Grant Macdonald is a British mathematician known for his contributions to symmetric functions, special functions, Lie algebra theory and other aspects of algebraic combinatorics ....
advises readers preferring the French convention to "read this book upside down in a mirror" (Macdonald 1979, p.2). This nomenclature probably started out as jocular. The English notation corresponds to the one universally used for matrices, while the French notation is closer to the convention of Cartesian coordinates; however, French notation differs from that convention by placing the vertical coordinate first. The figure on the right shows, using the English notation, the Young diagram corresponding to the partition (5, 4, 1) of the number 10. The conjugate partition, measuring the column lengths, is (3, 2, 2, 2, 1).
Tableaux
In other applications, it is natural to allow the same number to appear more than once (or not at all) in a tableau. A tableau is called semistandard, or column strict, if the entries weakly increase along each row and strictly increase down each column. Recording the number of times each number appears in a tableau gives a sequence known as the weight of the tableau. Thus the standard Young tableaux are precisely the semistandard tableaux of weight (1,1,...,1), which requires every integer up to to occur exactly once.
Variations
There are several variations of this definition: for example, in a row-strict tableau the entries strictly increase along the rows and weakly increase down the columns. Also, tableaux with decreasing entries have been considered, notably, in the theory of plane partitions. There are also generalizations such as domino tableaux or ribbon tableaux, in which several boxes may be grouped together before assigning entries to them.Skew tableaux
A skew shape is a pair of partitions such that the Young diagram of contains the Young diagram of ; it is denoted by /. If = and =, then the containment of diagrams means that ≤ for all . The skew diagram of a skew shape / is the set-theoretic difference of the Young diagrams of and : the set of squares that belong to the diagram of but not to that of . A skew tableau of shape / is obtained by filling the squares of the corresponding skew diagram; such a tableau is semistandard if entries increase weakly along each row, and increase strictly down each column, and it is standard if moreover all numbers from 1 to the number of squares of the skew diagram occur exactly once. While the map from partitions to their Young diagrams is injective, this is not the case from the map from skew shapes to skew diagrams; therefore the shape of a skew diagram cannot always be determined from the set of filled squares only. Although many properties of skew tableaux only depend on the filled squares, some operations defined on them do require explicit knowledge of and , so it is important that skew tableaux do record this information: two distinct skew tableaux may differ only in their shape, while they occupy the same set of squares, each filled with the same entries. Young tableaux can be identified with skew tableaux in which is the empty partition (0) (the unique partition of 0).Any skew semistandard tableau of shape / with positive integer entries gives rise to a sequence of partitions (or Young diagrams), by starting with , and taking for the partition places further in the sequence the one whose diagram is obtained from that of by adding all the boxes that contain a value ≤ in ; this partition eventually becomes equal to . Any pair of successive shapes in such a sequence is a skew shape whose diagram contains at most one box in each column; such shapes are called horizontal strips. This sequence of partitions completely determines , and it is in fact possible to define (skew) semistandard tableaux as such sequences, as is done by Macdonald (Macdonald 1979, p.4). Note that this definition incorporates the partitions and in the data comprising the skew tableau.
Overview of applications
Young tableaux have numerous applications in combinatoricsCombinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
, representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
, and algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
. Various ways of counting Young tableaux have been explored and lead to the definition of and identities for Schur functions. Many combinatorial algorithms on tableaux are known, including Schützenberger's jeu de taquin
Jeu de taquin
In the mathematical field of combinatorics, jeu de taquin is a construction due to which defines an equivalence relation on the set of skew standard Young tableaux. A jeu de taquin slide is a transformation where the numbers in a tableau are moved around in a way similar to how the pieces in the...
and the Robinson–Schensted–Knuth correspondence
Robinson–Schensted–Knuth correspondence
In mathematics, the Robinson–Schensted–Knuth correspondence, also referred to as the RSK correspondence or RSK algorithm, is a combinatorial bijection between matrices with non-negative integer entries and pairs of semistandard Young tableaux of equal shape, whose size equals the sum of the...
. Lascoux and Schützenberger studied an associative product on the set of all semistandard Young tableaux, giving it the structure called the plactic monoid (French: le monoïde plaxique).
In representation theory, standard Young tableaux of size describe bases in irreducible representations of the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
on letters. The standard monomial basis in a finite-dimensional irreducible representation of the general linear group
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
are parametrized by the set of semistandard Young tableaux of a fixed shape over the alphabet {1, 2, ..., }. This has important consequences for invariant theory
Invariant theory
Invariant theory is a branch of abstract algebra dealing with actions of groups on algebraic varieties from the point of view of their effect on functions...
, starting from the work of Hodge
W. V. D. Hodge
William Vallance Douglas Hodge FRS was a Scottish mathematician, specifically a geometer.His discovery of far-reaching topological relations between algebraic geometry and differential geometry—an area now called Hodge theory and pertaining more generally to Kähler manifolds—has been a major...
on the homogeneous coordinate ring
Homogeneous coordinate ring
In algebraic geometry, the homogeneous coordinate ring R of an algebraic variety V given as a subvariety of projective space of a given dimension N is by definition the quotient ring...
of the Grassmanian and further explored by Gian-Carlo Rota
Gian-Carlo Rota
Gian-Carlo Rota was an Italian-born American mathematician and philosopher.-Life:Rota was born in Vigevano, Italy...
with collaborators, de Concini and Procesi, and Eisenbud
David Eisenbud
David Eisenbud is an American mathematician. He is a professor of mathematics at the University of California, Berkeley and was Director of the Mathematical Sciences Research Institute from 1997 to 2007....
. The Littlewood–Richardson rule
Littlewood–Richardson rule
In mathematics, the Littlewood–Richardson rule is a combinatorial description of the coefficients that arise when decomposing a product of two Schur functions as a linear combination of other Schur functions. These coefficients are natural numbers, which the Littlewood–Richardson rule describes as...
describing (among other things) the decomposition of tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
s of irreducible representations of into irreducible components is formulated in terms of certain skew semistandard tableaux.
Applications to algebraic geometry center around Schubert calculus
Schubert calculus
In mathematics, Schubert calculus is a branch of algebraic geometry introduced in the nineteenth century by Hermann Schubert, in order to solve various counting problems of projective geometry...
on Grassmanians and flag varieties. Certain important cohomology classes can be represented by Schubert polynomial
Schubert polynomial
In mathematics, Schubert polynomials are generalizations of Schur polynomials that represent cohomology classes of Schubert cycles in flag varieties.They were introduced by and are named after Hermann Schubert.-Background:...
s and described in terms of Young tableaux.
Applications in representation theory
Young diagrams are in one-to-one correspondence with irreducible representations of the symmetric groupSymmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
over the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s. They provide a convenient way of specifying the Young symmetrizer
Young symmetrizer
In mathematics, a Young symmetrizer is an element of the group algebra of the symmetric group, constructed in such a way that the image of the element corresponds to an irreducible representation of the symmetric group over the complex numbers. A similar construction works over any field, and the...
s from which the irreducible representations
Representation theory of the symmetric group
In mathematics, the representation theory of the symmetric group is a particular case of the representation theory of finite groups, for which a concrete and detailed theory can be obtained. This has a large area of potential applications, from symmetric function theory to problems of quantum...
are built. Many facts about a representation can be deduced from the corresponding diagram. Below, we describe two examples: determining the dimension of a representation and restricted representations. In both cases, we will see that some properties of a representation can be determined by using just its diagram.
Young diagrams also parametrize the irreducible polynomial representations of the general linear group
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
(when they have at most nonempty rows), or the irreducible representations of the special linear group
Special linear group
In mathematics, the special linear group of degree n over a field F is the set of n×n matrices with determinant 1, with the group operations of ordinary matrix multiplication and matrix inversion....
(when they have at most nonempty rows), or the irreducible complex representations of the special unitary group
Special unitary group
The special unitary group of degree n, denoted SU, is the group of n×n unitary matrices with determinant 1. The group operation is that of matrix multiplication...
(again when they have at most nonempty rows). In these case semistandard tableaux with entries up to play a central role, rather than standard tableaux; in particular it is the number of those tableaux that determines the dimension of the representation.
Dimension of a representation
The dimension of the irreducible representation of the symmetric group corresponding to a partition of is equal to the number of different standard Young tableaux that can be obtained from the diagram of the representation. This number can be calculated by hook-length formula.A hook length of a box in Young diagram of shape is the number of boxes that are in the same row to the right of it plus those boxes in the same column below it, plus one (for the box itself). By the hook-length formula, the dimension of an irreducible representation is divided by the product of the hook lengths of all boxes in the diagram of the representation:
The figure on the right shows hook-lengths for all boxes in the diagram of the partition 10 = 5 + 4 + 1. Thus
Similarly, the dimension of the irreducible representation of corresponding to the partition λ of n (with at most r parts) is the number of semistandard Young tableaux of shape λ (containing only the entries from 1 to r), which is given by the hook-length formula:
where the index i gives the row and j the column of a box. For instance, for the partition (5,4,1) we get as dimension of the corresponding irreducible representation of (traversing the boxes by rows):
Restricted representations
A representation of the symmetric group on elements, is also a representation of the symmetric group on elements, . However, an irreducible representation of may not be irreducible for . Instead, it may be a direct sum of several representations that are irreducible for . These representations are then called the factors of the restricted representationRestricted representation
In mathematics, restriction is a fundamental construction in representation theory of groups. Restriction forms a representation of a subgroup from a representation of the whole group. Often the restricted representation is simpler to understand...
(see also induced representation
Induced representation
In mathematics, and in particular group representation theory, the induced representation is one of the major general operations for passing from a representation of a subgroup H to a representation of the group G itself. It was initially defined as a construction by Frobenius, for linear...
).
The question of determining this decomposition of the restricted representation of a given irreducible representation of Sn, corresponding to a partition of , is answered as follows. One forms the set of all Young diagrams that can be obtained from the diagram of shape by removing just one box (which must be at the end both of its row and of its column); the restricted representation then decomposes as a direct sum of the irreducible representations of corresponding to those diagrams, each occurring exactly once in the sum.
See also
- Robinson–Schensted correspondence
- Schur–Weyl dualitySchur–Weyl dualitySchur–Weyl duality is a mathematical theorem in representation theory that relates irreducible finite-dimensional representations of the general linear and symmetric groups...
- Young's latticeYoung's latticeIn mathematics, Young's lattice is a partially ordered set and a lattice that is formed by all integer partitions. It is named after Alfred Young, who in a series of papers On quantitative substitutional analysis developed representation theory of the symmetric group...
External links
- Eric W. Weisstein. "Ferrers Diagram". From MathWorld—A Wolfram Web Resource.
- Eric W. Weisstein. "Young Tableau." From MathWorld—A Wolfram Web Resource.