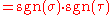Even and odd permutations
Encyclopedia
In mathematics
, when X is a finite set of at least two elements, the permutation
s of X (i.e. the bijective mappings from X to X) fall into two classes of equal size: the even permutations and the odd permutations. If any total ordering of X is fixed, the parity (oddness or evenness) of a permutation of X can be defined as the parity of the number of inversions for
of X can be defined as the parity of the number of inversions for  , i.e., of pairs of elements
, i.e., of pairs of elements  of X such that
of X such that  and
and  .
.
The sign or signature of a permutation is denoted sgn(σ) and defined as +1 if
is denoted sgn(σ) and defined as +1 if  is even and −1 if
is even and −1 if  is odd. The signature defines the alternating character
is odd. The signature defines the alternating character
of the symmetric group
Sn. Another notation for the sign of a permutation is given by the more general Levi-Civita symbol
( ), which is defined for all maps from X to X, and has value zero for non-bijective maps.
), which is defined for all maps from X to X, and has value zero for non-bijective maps.
The sign of a permutation can be explicitly expressed as
where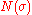 is the number of inversions in
is the number of inversions in  .
.
Alternatively, the sign of a permutation can be defined from its decomposition into the product of transpositions as
can be defined from its decomposition into the product of transpositions as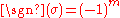
where m is the number of transpositions in the decomposition. Although such a decomposition is not unique, the parity of the number of transpositions in all decompositions is the same, implying that the sign of a permutation is well-defined
.
It can be obtained by three transpositions: first exchange the places of 1 and 3, then exchange the places of 2 and 4, and finally exchange the places of 1 and 5. This shows that the given permutation σ is odd. Using the notation explained in the permutation
article, we can write
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, when X is a finite set of at least two elements, the permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
s of X (i.e. the bijective mappings from X to X) fall into two classes of equal size: the even permutations and the odd permutations. If any total ordering of X is fixed, the parity (oddness or evenness) of a permutation
 of X can be defined as the parity of the number of inversions for
of X can be defined as the parity of the number of inversions for  , i.e., of pairs of elements
, i.e., of pairs of elements  of X such that
of X such that  and
and  .
.The sign or signature of a permutation
 is denoted sgn(σ) and defined as +1 if
is denoted sgn(σ) and defined as +1 if  is even and −1 if
is even and −1 if  is odd. The signature defines the alternating character
is odd. The signature defines the alternating characterCharacter (mathematics)
In mathematics, a character is a special kind of function from a group to a field . There are at least two distinct, but overlapping meanings...
of the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
Sn. Another notation for the sign of a permutation is given by the more general Levi-Civita symbol
Levi-Civita symbol
The Levi-Civita symbol, also called the permutation symbol, antisymmetric symbol, or alternating symbol, is a mathematical symbol used in particular in tensor calculus...
(
 ), which is defined for all maps from X to X, and has value zero for non-bijective maps.
), which is defined for all maps from X to X, and has value zero for non-bijective maps.The sign of a permutation can be explicitly expressed as

where
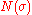 is the number of inversions in
is the number of inversions in  .
.Alternatively, the sign of a permutation
 can be defined from its decomposition into the product of transpositions as
can be defined from its decomposition into the product of transpositions as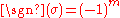
where m is the number of transpositions in the decomposition. Although such a decomposition is not unique, the parity of the number of transpositions in all decompositions is the same, implying that the sign of a permutation is well-defined
Well-defined
In mathematics, well-definition is a mathematical or logical definition of a certain concept or object which uses a set of base axioms in an entirely unambiguous way and satisfies the properties it is required to satisfy. Usually definitions are stated unambiguously, and it is clear they satisfy...
.
Example
Consider the permutation σ of the set {1,2,3,4,5} which turns the initial arrangement 12345 into 34521.It can be obtained by three transpositions: first exchange the places of 1 and 3, then exchange the places of 2 and 4, and finally exchange the places of 1 and 5. This shows that the given permutation σ is odd. Using the notation explained in the permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
article, we can write
-
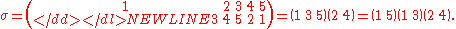
There are many other ways of writing σ as a composition of transpositions, for instance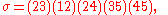
but it is impossible to write it as a product of an even number of transpositions.
Properties
The identity permutation is an even permutation. An even permutation can be obtained from the identity permutation by an even numberEven and odd numbersIn mathematics, the parity of an object states whether it is even or odd.This concept begins with integers. An even number is an integer that is "evenly divisible" by 2, i.e., divisible by 2 without remainder; an odd number is an integer that is not evenly divisible by 2...
of exchanges (called transpositions) of two elements, while an odd permutation can be obtained by an odd number of transpositions.
The following rules follow directly from the corresponding rules about addition of integers:- the composition of two even permutations is even
- the composition of two odd permutations is even
- the composition of an odd and an even permutation is odd
From these it follows that- the inverse of every even permutation is even
- the inverse of every odd permutation is odd
Considering the symmetric groupSymmetric groupIn mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
Sn of all permutations of the set {1,...,n}, we can conclude that the map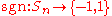
that assigns to every permutation its signature is a group homomorphismGroup homomorphismIn mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
.
Furthermore, we see that the even permutations form a subgroupSubgroupIn group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of Sn. This is the alternating group on n letters, denoted by An. It is the kernelKernel (algebra)In the various branches of mathematics that fall under the heading of abstract algebra, the kernel of a homomorphism measures the degree to which the homomorphism fails to be injective. An important special case is the kernel of a matrix, also called the null space.The definition of kernel takes...
of the homomorphism sgn. The odd permutations cannot form a subgroup, since the composite of two odd permutations is even, but they form a cosetCosetIn mathematics, if G is a group, and H is a subgroup of G, and g is an element of G, thenA coset is a left or right coset of some subgroup in G...
of An (in Sn).
If n>1, then there are just as many even permutations in Sn as there are odd ones; consequently, An contains n!FactorialIn mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
/2 permutations. [The reason: if σ is even, then (12)σ is odd; if σ is odd, then (12)σ is even; the two maps are inverse to each other.]
A cycleCycle (mathematics)In mathematics, and in particular in group theory, a cycle is a permutation of the elements of some set X which maps the elements of some subset S to each other in a cyclic fashion, while fixing all other elements...
is even if and only if its length is odd. This follows from formulas like = (a e) (b e) (c e) (d e)
In practice, in order to determine whether a given permutation is even or odd, one writes the permutation as a product of disjoint cycles. The permutation is odd if and only if this factorization contains an odd number of even-length cycles.
Another method for determining whether a given permutation is even or odd is to construct the corresponding Permutation matrixPermutation matrixIn mathematics, in matrix theory, a permutation matrix is a square binary matrix that has exactly one entry 1 in each row and each column and 0s elsewhere...
and compute its determinant. The value of the determinant is same as the parity of the permutation.
Every permutation of odd orderOrder (group theory)In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
must be even; the converse is not true in general.
Proof 1
Every permutation can be produced by a sequence of transpositions (2-element exchanges): with the first transposition we put the first element of the permutation in its proper place, the second transposition puts the second element right etc. Given a permutation σ, we can write it as a product of transpositions in many different ways. We want to show that either all of those decompositions have an even number of transpositions, or all have an odd number.
Suppose we have two such decompositions:- σ = T1 T2 ... Tk
- σ = Q1 Q2 ... Qm.
We want to show that k and m are either both even, or both odd.
Every transposition can be written as a product of an odd number of transpositions of adjacent elements, e.g. = (2 3)(3 4)(4 5)(4 3)(3 2)
If we decompose in this way each of the transpositions T1...Tk and Q1...Qm above
into an odd number of adjacent transpositions, we get the new decompositions:- σ = T1' T2' ... Tk'
- σ = Q1' Q2' ... Qm'
where all of the T1'...Tk' Q1'...Qm' are adjacent, k − k' is even, and m − m' is even.
Now compose the inverse of T1 with σ. T1 is the transposition (i, i + 1) of two adjacent numbers, so, compared to σ, the new permutation σ(i, i + 1) will have exactly one inversion pair less (in case (i,i + 1) was an inversion pair for σ) or more (in case (i, i + 1) was not an inversion pair). Then apply the inverses of T2, T3, ... Tk in the same way, "unraveling" the permutation σ. At the end we get the identity permutation, whose N is zero. This means that the original N(σ) less k is even.
We can do the same thing with the other decomposition, Q1...Qm, and it will turn out that the original N(σ) less m is even.
Therefore, m − k is even, as we wanted to show.
We can now define the permutation σ to be even if N(σ) is an even number, and odd if N(σ) is odd. This coincides with the definition given earlier but it is now clear that every permutation is either even or odd.
Proof 2
An alternative proof uses the polynomialPolynomialIn mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
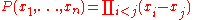
So for instance in the case n = 3, we have

Now for a given permutation σ of the numbers {1,...,n}, we define
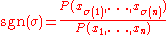
Since the polynomial has the same factors as
has the same factors as  except for their signs, if follows that sgn(σ) is either +1 or −1. Furthermore, if σ and τ are two permutations, we see that
except for their signs, if follows that sgn(σ) is either +1 or −1. Furthermore, if σ and τ are two permutations, we see that
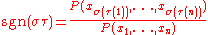
Since with this definition it is furthermore clear that any transposition of two adjacent elements has signature −1, we do indeed recover the signature as defined earlier.
Proof 3
A third approach uses the presentationPresentation of a groupIn mathematics, one method of defining a group is by a presentation. One specifies a set S of generators so that every element of the group can be written as a product of powers of some of these generators, and a set R of relations among those generators...
of the group Sn in terms of generators and relations
and relations
-
 for all i
for all i -
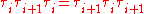 for all i < n − 1
for all i < n − 1 -
 if |i − j| ≥ 2.
if |i − j| ≥ 2.
[Here the generator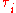 represents the transposition (i, i + 1).] All relations keep the length of a word the same or change it by two. Starting with an even-length word will thus always result in an even-length word after using the relations, and similarly for odd-length words. It is therefore unambiguous to call the elements of Sn represented by even-length words "even", and the elements represented by odd-length words "odd".
represents the transposition (i, i + 1).] All relations keep the length of a word the same or change it by two. Starting with an even-length word will thus always result in an even-length word after using the relations, and similarly for odd-length words. It is therefore unambiguous to call the elements of Sn represented by even-length words "even", and the elements represented by odd-length words "odd".
Generalizations
Parity can be generalized to Coxeter groupCoxeter groupIn mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
s: one defines a length functionLength functionIn mathematical field of geometric group theory, a length function is a function that assigns a number to each element of a group.-Definition:...
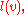 which depends on a choice of generators (for the symmetric group, adjacent transpositions), and then the function
which depends on a choice of generators (for the symmetric group, adjacent transpositions), and then the function 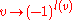 gives a generalized sign map.
gives a generalized sign map.
See also
- The fifteen puzzle is a classic application, though it actually involves a groupoidGroupoidIn mathematics, especially in category theory and homotopy theory, a groupoid generalises the notion of group in several equivalent ways. A groupoid can be seen as a:...
. - Zolotarev's lemmaZolotarev's lemmaIn number theory, Zolotarev's lemma states that the Legendre symbol\leftfor an integer a modulo an odd prime number p, where p does not divide a, can be computed as the sign of a permutation:...