
Symmetrization
Encyclopedia
In mathematics
, symmetrization is a process that converts any function in n variables to a symmetric function
in n variables.
Conversely, anti-symmetrization converts any function in n variables into an antisymmetric
function.
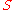 be a set and
be a set and  an Abelian group
an Abelian group
. Given a map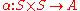 ,
,  is termed a symmetric map if
is termed a symmetric map if 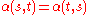 for all
for all 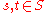 .
.
The symmetrization of a map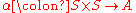 is the map
is the map 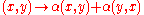 .
.
Conversely, the anti-symmetrization or skew-symmetrization of a map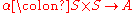 is the map
is the map 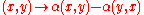 .
.
The sum of the symmetrization and the anti-symmetrization is
Thus, away from 2, meaning if 2 is invertible, such as for the real numbers, one can divide by 2 and express every function as a sum of a symmetric function and an anti-symmetric function.
The symmetrization of a symmetric map is simply its double, while the symmetrization of an alternating map is zero; similarly, the anti-symmetrization of a symmetric map is zero, while the anti-symmetrization of an anti-symmetric map is its double.
At 2, not every form can be decomposed into a symmetric form and a skew-symmetric form – for instance, over the integers, the associated symmetric form (over the rationals) may take half-integer values, while over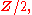 a function is skew-symmetric if and only if it is symmetric (as
a function is skew-symmetric if and only if it is symmetric (as 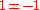 ).
).
This leads to the notion of ε-quadratic forms and ε-symmetric forms.
:
As the symmetric group of order two equals the cyclic group
of order two ( ), this corresponds to the discrete Fourier transform
), this corresponds to the discrete Fourier transform
of order two.
 permutations of the variables, or anti-symmetrize by taking the sum over all
permutations of the variables, or anti-symmetrize by taking the sum over all 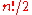 even permutations and subtracting the sum over all
even permutations and subtracting the sum over all 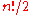 odd permutations.
odd permutations.
Here symmetrizing (respectively anti-symmetrizing) a symmetric (respectively anti-symmetric) function multiplies by n! – thus if n! is invertible, such as if one is working over the rationals or over a field of characteristic then these yield projections.
then these yield projections.
In terms of representation theory, these only yield the subrepresentations corresponding to the trivial and sign representation, but for there are others – see representation theory of the symmetric group
there are others – see representation theory of the symmetric group
and symmetric polynomials.
, and the associated statistics are called U-statistics.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, symmetrization is a process that converts any function in n variables to a symmetric function
Symmetric function
In algebra and in particular in algebraic combinatorics, the ring of symmetric functions, is a specific limit of the rings of symmetric polynomials in n indeterminates, as n goes to infinity...
in n variables.
Conversely, anti-symmetrization converts any function in n variables into an antisymmetric
Antisymmetric
The word antisymmetric refers to a change to an opposite quantity when another quantity is symmetrically changed. This concept is related to that of Symmetry and Asymmetry. The difference between these three concepts can be simply illustrated with Latin letters. The character "A" is symmetric about...
function.
2 variables
Let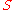 be a set and
be a set and  an Abelian group
an Abelian groupAbelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
. Given a map
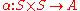 ,
,  is termed a symmetric map if
is termed a symmetric map if 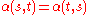 for all
for all 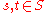 .
.The symmetrization of a map
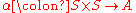 is the map
is the map 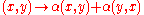 .
.Conversely, the anti-symmetrization or skew-symmetrization of a map
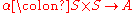 is the map
is the map 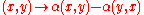 .
.The sum of the symmetrization and the anti-symmetrization is

Thus, away from 2, meaning if 2 is invertible, such as for the real numbers, one can divide by 2 and express every function as a sum of a symmetric function and an anti-symmetric function.
The symmetrization of a symmetric map is simply its double, while the symmetrization of an alternating map is zero; similarly, the anti-symmetrization of a symmetric map is zero, while the anti-symmetrization of an anti-symmetric map is its double.
Bilinear forms
The symmetrization and anti-symmetrization of a bilinear map are bilinear; thus away from 2, every bilinear form is a sum of a symmetric form and a skew-symmetric form, and there is no difference between a symmetric form and a quadratic form.At 2, not every form can be decomposed into a symmetric form and a skew-symmetric form – for instance, over the integers, the associated symmetric form (over the rationals) may take half-integer values, while over
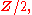 a function is skew-symmetric if and only if it is symmetric (as
a function is skew-symmetric if and only if it is symmetric (as 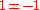 ).
).This leads to the notion of ε-quadratic forms and ε-symmetric forms.
Representation theory
In terms of representation theoryRepresentation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
:
- exchanging variables gives a representation of the symmetric groupSymmetric groupIn mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
on the space of functions in two variables, - the symmetric and anti-symmetric functions are the subrepresentations corresponding to the trivial representationTrivial representationIn the mathematical field of representation theory, a trivial representation is a representation of a group G on which all elements of G act as the identity mapping of V...
and the sign representation, and - symmetrization and anti-symmetrization map a function into these subrepresentations – if one divides by 2, these yield projection maps.
As the symmetric group of order two equals the cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
of order two (
 ), this corresponds to the discrete Fourier transform
), this corresponds to the discrete Fourier transformDiscrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
of order two.
n variables
More generally, given a function in n variables, one can symmetrize by taking the sum over all permutations of the variables, or anti-symmetrize by taking the sum over all
permutations of the variables, or anti-symmetrize by taking the sum over all 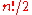 even permutations and subtracting the sum over all
even permutations and subtracting the sum over all 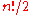 odd permutations.
odd permutations.Here symmetrizing (respectively anti-symmetrizing) a symmetric (respectively anti-symmetric) function multiplies by n! – thus if n! is invertible, such as if one is working over the rationals or over a field of characteristic
 then these yield projections.
then these yield projections.In terms of representation theory, these only yield the subrepresentations corresponding to the trivial and sign representation, but for
 there are others – see representation theory of the symmetric group
there are others – see representation theory of the symmetric groupRepresentation theory of the symmetric group
In mathematics, the representation theory of the symmetric group is a particular case of the representation theory of finite groups, for which a concrete and detailed theory can be obtained. This has a large area of potential applications, from symmetric function theory to problems of quantum...
and symmetric polynomials.
Bootstrapping
Given a function in k variables, one can obtain a symmetric function in n variables by taking the sum over k element subsets of the variables. In statistics, this is referred to as bootstrappingBootstrapping (statistics)
In statistics, bootstrapping is a computer-based method for assigning measures of accuracy to sample estimates . This technique allows estimation of the sample distribution of almost any statistic using only very simple methods...
, and the associated statistics are called U-statistics.

