Symmetric inverse semigroup
Encyclopedia
In modern algebra, the set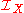 
of all partial one-one transformations on a set X forms an inverse semigroup
, called
the symmetric inverse semigroup (or monoid) on X. In general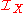
is not commutative. More details are available in the discussion on the origins of the inverse semigroup.
.
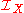of all partial one-one transformations on a set X forms an inverse semigroupInverse semigroup
In mathematics, an inverse semigroup S is a semigroup in which every element x in S has a unique inversey in S in the sense that x = xyx and y = yxy...
, called
the symmetric inverse semigroup (or monoid) on X. In general
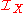is not commutative. More details are available in the discussion on the origins of the inverse semigroup.Finite symmetric inverse semigroups
When X is a finite set {1, ..., n}, the inverse semigroup of one-one partial transformations is denoted by Cn and its elements are called charts. The notion of chart generalizes the notion of permutationPermutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
.