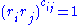Reflection group
Encyclopedia
In group theory
and geometry
, a reflection group is a discrete group
which is generated by a set of reflections
of a finite-dimensional Euclidean space
. The symmetry group of a regular polytope
or of a tiling
of the Euclidean space by congruent copies of a regular polytope is necessarily a reflection group. Reflection groups also include Weyl group
s and crystallographic Coxeter group
s. While the orthogonal group
is generated by reflections (by the Cartan–Dieudonné theorem), it is a continuous group (indeed, Lie group
), not a discrete group, and is generally considered separately.
. finite reflection group is a subgroup of the general linear group
of E which is generated by a set of orthogonal reflection
s across hyperplanes passing through the origin. An affine reflection group is a discrete subgroup of the affine group
of E that is generated by a set of affine reflections of E (without the requirement that the reflection hyperplanes pass through the origin).
The corresponding notions can be defined over other fields
, leading to complex reflection group
s and analogues of reflection groups over a finite field
.
s, which are generated by reflection in two lines that form an angle of
and correspond to the Coxeter diagram 
Conversely, the cyclic point groups in two dimensions
are not generated by reflections, and indeed contain no reflections – they are however subgroups of index 2 of a dihedral group.
Infinite reflection groups include the frieze group
s
and 
and the wallpaper group
s pmm, p3m1, p4m, and p6m. If the angle between two lines is an irrational multiple of pi, the group generated by reflections in these lines is infinite and non-discrete, hence, it is not a reflection group.
Cnv, Dnh, and the symmetry group
s of the five Platonic solid
s. Dual regular polyhedra (cube and octahedron, as well as dodecahedron and icosahedron) give rise to isomorphic symmetry groups. The classification of finite reflection groups of R3 is an instance of the ADE classification
.
s, as discussed in .
"chamber" are generators ri of W of order 2. All relations between them formally follow from the relations
expressing the fact that the product of the reflections ri and rj in two hyperplanes Hi and Hj meeting at an angle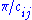
is a rotation
by the angle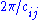
fixing the subspace Hi ∩ Hj of codimension 2. Thus, viewed as an abstract group, every reflection group is a Coxeter group
.
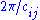so reflections are the identity). Geometrically, this amounts to including shears in a hyperplane. In characteristic 2, using the above fixed-hyperplane definition of "reflection," it is no longer true that every finite reflection group is a Coxeter group. See A simple reflection group of order 168. Reflection groups over finite fields of characteristic not 2 were classified in .
s of more general Riemannian manifold
s generated by reflections have also been considered. The most important class arises from Riemannian symmetric space
s of rank 1: the n-sphere Sn, corresponding to finite reflection groups, the Euclidean space Rn, corresponding to
affine reflection groups, and the hyperbolic space
Hn, where the corresponding groups are called hyperbolic reflection groups. In two dimensions, triangle group
s include reflection groups of all three kinds.
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
and geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a reflection group is a discrete group
Discrete group
In mathematics, a discrete group is a group G equipped with the discrete topology. With this topology G becomes a topological group. A discrete subgroup of a topological group G is a subgroup H whose relative topology is the discrete one...
which is generated by a set of reflections
Reflection (mathematics)
In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection...
of a finite-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
. The symmetry group of a regular polytope
Regular polytope
In mathematics, a regular polytope is a polytope whose symmetry is transitive on its flags, thus giving it the highest degree of symmetry. All its elements or j-faces — cells, faces and so on — are also transitive on the symmetries of the polytope, and are regular polytopes of...
or of a tiling
Tessellation
A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...
of the Euclidean space by congruent copies of a regular polytope is necessarily a reflection group. Reflection groups also include Weyl group
Weyl group
In mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection...
s and crystallographic Coxeter group
Coxeter group
In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
s. While the orthogonal group
Orthogonal group
In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
is generated by reflections (by the Cartan–Dieudonné theorem), it is a continuous group (indeed, Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
), not a discrete group, and is generally considered separately.
Definition
Let E be a finite-dimensional Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
. finite reflection group is a subgroup of the general linear group
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
of E which is generated by a set of orthogonal reflection
Reflection (mathematics)
In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection...
s across hyperplanes passing through the origin. An affine reflection group is a discrete subgroup of the affine group
Affine group
In mathematics, the affine group or general affine group of any affine space over a field K is the group of all invertible affine transformations from the space into itself.It is a Lie group if K is the real or complex field or quaternions....
of E that is generated by a set of affine reflections of E (without the requirement that the reflection hyperplanes pass through the origin).
The corresponding notions can be defined over other fields
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
, leading to complex reflection group
Complex reflection group
In mathematics, a complex reflection group is a group acting on a finite-dimensional complex vector space, that is generated by complex reflections: non-trivial elements that fix a complex hyperplane in space pointwise...
s and analogues of reflection groups over a finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
.
Plane
In two dimensions, the finite reflection groups are the dihedral groupDihedral group
In mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
s, which are generated by reflection in two lines that form an angle of
and correspond to the Coxeter diagram 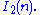Conversely, the cyclic point groups in two dimensionsPoint groups in two dimensions
In geometry, a two-dimensional point group or rosette group is a group of geometric symmetries that keep at least one point fixed in a plane. Every such group is a subgroup of the orthogonal group O, including O itself...
are not generated by reflections, and indeed contain no reflections – they are however subgroups of index 2 of a dihedral group.
Infinite reflection groups include the frieze group
Frieze group
A frieze group is a mathematical concept to classify designs on two-dimensional surfaces which are repetitive in one direction, based on the symmetries in the pattern. Such patterns occur frequently in architecture and decorative art...
s
and and the wallpaper groupWallpaper group
A wallpaper group is a mathematical classification of a two-dimensional repetitive pattern, based on the symmetries in the pattern. Such patterns occur frequently in architecture and decorative art...
s pmm, p3m1, p4m, and p6m. If the angle between two lines is an irrational multiple of pi, the group generated by reflections in these lines is infinite and non-discrete, hence, it is not a reflection group.
Space
Finite reflection groups are the point groupsPoint groups in three dimensions
In geometry, a point group in three dimensions is an isometry group in three dimensions that leaves the origin fixed, or correspondingly, an isometry group of a sphere. It is a subgroup of the orthogonal group O, the group of all isometries that leave the origin fixed, or correspondingly, the group...
Cnv, Dnh, and the symmetry group
Symmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
s of the five Platonic solid
Platonic solid
In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...
s. Dual regular polyhedra (cube and octahedron, as well as dodecahedron and icosahedron) give rise to isomorphic symmetry groups. The classification of finite reflection groups of R3 is an instance of the ADE classification
ADE classification
In mathematics, the ADE classification is the complete list of simply laced Dynkin diagrams or other mathematical objects satisfying analogous axioms; "simply laced" means that there are no multiple edges, which corresponds to all simple roots in the root system forming angles of \pi/2 = 90^\circ ...
.
Kaleidoscopes
Reflection groups have deep relations with kaleidoscopeKaleidoscope
A kaleidoscope is a circle of mirrors containing loose, colored objects such as beads or pebbles and bits of glass. As the viewer looks into one end, light entering the other end creates a colorful pattern, due to the reflection off the mirrors...
s, as discussed in .
Relation with Coxeter groups
A reflection group W admits a presentation of a special kind discovered and studied by H.S.M. Coxeter. The reflections in the faces of a fixed fundamentalFundamental domain
In geometry, the fundamental domain of a symmetry group of an object is a part or pattern, as small or irredundant as possible, which determines the whole object based on the symmetry. More rigorously, given a topological space and a group acting on it, the images of a single point under the group...
"chamber" are generators ri of W of order 2. All relations between them formally follow from the relations
expressing the fact that the product of the reflections ri and rj in two hyperplanes Hi and Hj meeting at an angle
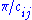is a rotationRotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
by the angle
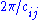fixing the subspace Hi ∩ Hj of codimension 2. Thus, viewed as an abstract group, every reflection group is a Coxeter groupCoxeter group
In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
.
Finite fields
When working over finite fields, one defines a "reflection" as a map that fixes a hyperplane (otherwise for example there would be no reflections in characteristic 2, as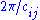 so reflections are the identity). Geometrically, this amounts to including shears in a hyperplane. In characteristic 2, using the above fixed-hyperplane definition of "reflection," it is no longer true that every finite reflection group is a Coxeter group. See A simple reflection group of order 168. Reflection groups over finite fields of characteristic not 2 were classified in .Generalizations
Discrete isometry groupIsometry group
In mathematics, the isometry group of a metric space is the set of all isometries from the metric space onto itself, with the function composition as group operation...
s of more general Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
s generated by reflections have also been considered. The most important class arises from Riemannian symmetric space
Riemannian symmetric space
In differential geometry, representation theory and harmonic analysis, a symmetric space is a smooth manifold whose group of symmetries contains an inversion symmetry about every point. There are two ways to formulate the inversion symmetry, via Riemannian geometry or via Lie theory...
s of rank 1: the n-sphere Sn, corresponding to finite reflection groups, the Euclidean space Rn, corresponding to
affine reflection groups, and the hyperbolic space
Hyperbolic space
In mathematics, hyperbolic space is a type of non-Euclidean geometry. Whereas spherical geometry has a constant positive curvature, hyperbolic geometry has a negative curvature: every point in hyperbolic space is a saddle point...
Hn, where the corresponding groups are called hyperbolic reflection groups. In two dimensions, triangle group
Triangle group
In mathematics, a triangle group is a group that can be realized geometrically by sequences of reflections across the sides of a triangle. The triangle can be an ordinary Euclidean triangle, a triangle on the sphere, or a hyperbolic triangle...
s include reflection groups of all three kinds.