Characteristic subgroup
Encyclopedia
In mathematics
, particularly in the area of abstract algebra
known as group theory
, a characteristic subgroup is a subgroup
that is invariant
under all automorphism
s of the parent group
. Because conjugation
is an automorphism, every characteristic subgroup is normal
, though not every normal subgroup is characteristic. Examples of characteristic subgroups include the commutator subgroup
and the center of a group.
G is a subgroup
H that is invariant under each automorphism
of G. That is,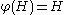
for every automorphism φ of G (where φ(H) denotes the image
of H under φ).
The statement “H is a characteristic subgroup of G” is written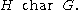
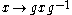
is an automorphism of G (known as an inner automorphism
). A subgroup of G that is invariant under all inner automorphisms is called normal
. Since a characteristic subgroup is invariant under all automorphisms, every characteristic subgroup is normal.
Not every normal subgroup is characteristic. Here are several examples:
Note: If H is the unique subgroup of a group G, then H is characteristic in G.
s. For a finite group
this is the same, because surjectivity implies injectivity, but not for an infinite group: a surjective endomorphism is not necessarily an automorphism.
(also called a fully invariant subgroup) H of a group G is a group remaining invariant under every endomorphism of G; in other words, if f : G → G is any homomorphism
, then f(H) is a subgroup of H.
, which is the image of a fully invariant subgroup of a free group
under a homomorphism.
The center of a group is easily seen to always be a distinguished subgroup, but it is not always fully characteristic. The finite group of order 12, Sym(3) × Z/2Z has a homomorphism taking (π, y) to ( (1,2)y, 0) which takes the center 1 × Z/2Z into a subgroup of Sym(3) × 1, which meets the center only in the identity.
The relationship amongst these subgroup properties can be expressed as:
of order 6 and a cyclic group
of order 2). The center of G is its second factor Z2. Note that the first factor S3 contains subgroups isomorphic to Z2, for instance {identity,(12)}; let f: Z2 → S3 be the morphism mapping Z2 onto the indicated subgroup. Then the composition of the projection of G onto its second factor Z2, followed by f, followed by the inclusion of S3 into G as its first factor, provides an endomorphism of G under which the image of the center Z2 is not contained in the center, so here the center is not a fully characteristic subgroup of G.
of an abelian group
is a fully invariant subgroup.
; if H is a (fully) characteristic subgroup of K, and K is a (fully) characteristic subgroup of G, then H is a (fully) characteristic subgroup of G.
Moreover, while it is not true that every normal subgroup of a normal subgroup is normal, it is true that every characteristic subgroup of a normal subgroup is normal. Similarly, while it is not true that every distinguished subgroup of a distinguished subgroup is distinguished, it is true that every fully characteristic subgroup of a distinguished subgroup is distinguished.
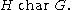, then every automorphism of G induces an automorphism of the quotient group G/H, which yields a map 
.
If H is fully characteristic in G, then analogously, every endomorphism of G induces an endomorphism of G/H, which yields a map
.
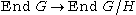Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, particularly in the area of abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
known as group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, a characteristic subgroup is a subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
that is invariant
Invariant (mathematics)
In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
under all automorphism
Automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
s of the parent group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
. Because conjugation
Inner automorphism
In abstract algebra an inner automorphism is a functionwhich, informally, involves a certain operation being applied, then another one performed, and then the initial operation being reversed...
is an automorphism, every characteristic subgroup is normal
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
, though not every normal subgroup is characteristic. Examples of characteristic subgroups include the commutator subgroup
Commutator subgroup
In mathematics, more specifically in abstract algebra, the commutator subgroup or derived subgroup of a group is the subgroup generated by all the commutators of the group....
and the center of a group.
Definitions
A characteristic subgroup of a groupGroup (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
G is a subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
H that is invariant under each automorphism
Automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
of G. That is,
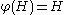
for every automorphism φ of G (where φ(H) denotes the image
Image (mathematics)
In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
of H under φ).
The statement “H is a characteristic subgroup of G” is written
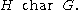
Characteristic vs. normal
If G is a group, and g is a fixed element of G, then the conjugation map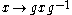is an automorphism of G (known as an inner automorphism
Inner automorphism
In abstract algebra an inner automorphism is a functionwhich, informally, involves a certain operation being applied, then another one performed, and then the initial operation being reversed...
). A subgroup of G that is invariant under all inner automorphisms is called normal
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
. Since a characteristic subgroup is invariant under all automorphisms, every characteristic subgroup is normal.
Not every normal subgroup is characteristic. Here are several examples:
- Let H be a group, and let G be the direct productDirect product of groupsIn the mathematical field of group theory, the direct product is an operation that takes two groups and and constructs a new group, usually denoted...
H × H. Then the subgroups {1} × H and H × {1} are both normal, but neither is characteristic. In particular, neither of these subgroups is invariant under the automorphism (x, y) → (y, x) that switches the two factors. - For a concrete example of this, let V be the Klein four-groupKlein four-groupIn mathematics, the Klein four-group is the group Z2 × Z2, the direct product of two copies of the cyclic group of order 2...
(which is isomorphicGroup isomorphismIn abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic...
to the direct product Z2Cyclic groupIn group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
× Z2Cyclic groupIn group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
). Since this group is abelianAbelian groupIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
, every subgroup is normal; but every permutation of the three non-identity elements is an automorphism of V, so the three subgroups of order 2 are not characteristic.Here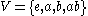
Consider H={e,a} and consider the automorphism 
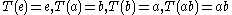.Then T(H) is not contained in H. - In the quaternion groupQuaternion groupIn group theory, the quaternion group is a non-abelian group of order eight, isomorphic to a certain eight-element subset of the quaternions under multiplication...
of order 8, each of the cyclic subgroups of order 4 is normal, but none of these are characteristic. However, the subgroup {1, −1} is characteristic, since it is the only subgroup of order 2.
Note: If H is the unique subgroup of a group G, then H is characteristic in G.
- If n is even, the dihedral groupDihedral groupIn mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
of order 2n has three subgroups of indexIndex of a subgroupIn mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
two, all of which are normal. One of these is the cyclic subgroup, which is characteristic. The other two subgroups are dihedral; these are permuted by an outer automorphismOuter automorphism groupIn mathematics, the outer automorphism group of a group Gis the quotient Aut / Inn, where Aut is the automorphism group of G and Inn is the subgroup consisting of inner automorphisms. The outer automorphism group is usually denoted Out...
of the parent group, and are therefore not characteristic. - "Normality" is not transitive but Characteristic is transitive. If H Char K and K normal in G then H normal in G.
Distinguished subgroups
A related concept is that of a distinguished subgroup. In this case the subgroup H is invariant under the applications of surjective endomorphismEndomorphism
In mathematics, an endomorphism is a morphism from a mathematical object to itself. For example, an endomorphism of a vector space V is a linear map ƒ: V → V, and an endomorphism of a group G is a group homomorphism ƒ: G → G. In general, we can talk about...
s. For a finite group
Finite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
this is the same, because surjectivity implies injectivity, but not for an infinite group: a surjective endomorphism is not necessarily an automorphism.
Fully invariant subgroups
For an even stronger constraint, a fully characteristic subgroupFully characteristic subgroup
In mathematics, a subgroup of a group is fully characteristic if it is invariant under every endomorphism of the group. That is, any endomorphism of the group takes elements of the subgroup to elements of the subgroup....
(also called a fully invariant subgroup) H of a group G is a group remaining invariant under every endomorphism of G; in other words, if f : G → G is any homomorphism
Group homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
, then f(H) is a subgroup of H.
Verbal subgroups
An even stronger constraint is verbal subgroupVerbal subgroup
In mathematics, especially in the area of abstract algebra known as group theory, a verbal subgroup is a special sort of subgroup of a group that can be defined as all elements that can be expressed as products of a special form, called a word...
, which is the image of a fully invariant subgroup of a free group
Free group
In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
under a homomorphism.
Containments
Every subgroup that is fully characteristic is certainly distinguished and therefore characteristic; but a characteristic or even distinguished subgroup need not be fully characteristic.The center of a group is easily seen to always be a distinguished subgroup, but it is not always fully characteristic. The finite group of order 12, Sym(3) × Z/2Z has a homomorphism taking (π, y) to ( (1,2)y, 0) which takes the center 1 × Z/2Z into a subgroup of Sym(3) × 1, which meets the center only in the identity.
The relationship amongst these subgroup properties can be expressed as:
- subgroupSubgroupIn group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
⇐ normal subgroupNormal subgroupIn abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
⇐ characteristic subgroup ⇐ distinguished subgroup ⇐ fully characteristic subgroupFully characteristic subgroupIn mathematics, a subgroup of a group is fully characteristic if it is invariant under every endomorphism of the group. That is, any endomorphism of the group takes elements of the subgroup to elements of the subgroup....
⇐ verbal subgroupVerbal subgroupIn mathematics, especially in the area of abstract algebra known as group theory, a verbal subgroup is a special sort of subgroup of a group that can be defined as all elements that can be expressed as products of a special form, called a word...
Finite example
Consider the group G = S3 × Z2 (the group of order 12 which is the direct product of the symmetric groupSymmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
of order 6 and a cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
of order 2). The center of G is its second factor Z2. Note that the first factor S3 contains subgroups isomorphic to Z2, for instance {identity,(12)}; let f: Z2 → S3 be the morphism mapping Z2 onto the indicated subgroup. Then the composition of the projection of G onto its second factor Z2, followed by f, followed by the inclusion of S3 into G as its first factor, provides an endomorphism of G under which the image of the center Z2 is not contained in the center, so here the center is not a fully characteristic subgroup of G.
Subgroup functors
The derived subgroup (or commutator subgroup) of a group is a verbal subgroup. The torsion subgroupTorsion subgroup
In the theory of abelian groups, the torsion subgroup AT of an abelian group A is the subgroup of A consisting of all elements that have finite order...
of an abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
is a fully invariant subgroup.
Transitivity
The property of being characteristic or fully characteristic is transitiveTransitivity (mathematics)
-In grammar:* Intransitive verb* Transitive verb, when a verb takes an object* Transitivity -In logic and mathematics:* Arc-transitive graph* Edge-transitive graph* Ergodic theory, a group action that is metrically transitive* Vertex-transitive graph...
; if H is a (fully) characteristic subgroup of K, and K is a (fully) characteristic subgroup of G, then H is a (fully) characteristic subgroup of G.
Moreover, while it is not true that every normal subgroup of a normal subgroup is normal, it is true that every characteristic subgroup of a normal subgroup is normal. Similarly, while it is not true that every distinguished subgroup of a distinguished subgroup is distinguished, it is true that every fully characteristic subgroup of a distinguished subgroup is distinguished.
Map on Aut and End
If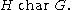, then every automorphism of G induces an automorphism of the quotient group G/H, which yields a map .If H is fully characteristic in G, then analogously, every endomorphism of G induces an endomorphism of G/H, which yields a map
.
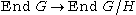