
Equilateral triangle
Overview
| angle = 60°
}}
In geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, an equilateral triangle is a triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
in which all three sides are equal. In traditional or Euclidean geometry
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
, equilateral triangles are also equiangular
Equiangular polygon
In Euclidean geometry, an equiangular polygon is a polygon whose vertex angles are equal. If the lengths of the sides are also equal then it is a regular polygon.The only equiangular triangle is the equilateral triangle...
; that is, all three internal angles are also congruent to each other and are each 60°. They are regular polygon
Regular polygon
A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...
s, and can therefore also be referred to as regular triangles.
A triangle that has the sides a, b, c, and where R and r are the radii of the circumcircle and incircle
Incircle and excircles of a triangle
In geometry, the incircle or inscribed circle of a triangle is the largest circle contained in the triangle; it touches the three sides...
respectively, is equilateral if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
it satisfies any one of the following necessary and sufficient conditions:
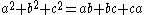
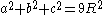

- the circumcenterCircumscribed circleIn geometry, the circumscribed circle or circumcircle of a polygon is a circle which passes through all the vertices of the polygon. The center of this circle is called the circumcenter....
coincides with the incenterIncircle and excircles of a triangleIn geometry, the incircle or inscribed circle of a triangle is the largest circle contained in the triangle; it touches the three sides...
. - the circumcenter coincides with the orthocenterAltitude (triangle)In geometry, an altitude of a triangle is a straight line through a vertex and perpendicular to a line containing the base . This line containing the opposite side is called the extended base of the altitude. The intersection between the extended base and the altitude is called the foot of the...
. - the circumcenter coincides with the centroidCentroidIn geometry, the centroid, geometric center, or barycenter of a plane figure or two-dimensional shape X is the intersection of all straight lines that divide X into two parts of equal moment about the line. Informally, it is the "average" of all points of X...
. - the circumcenter coincides with the Nagel pointNagel pointIn geometry, the Nagel point is a point associated with any triangle. Given a triangle ABC, let TA, TB, and TC be the extouch points in which the A-excircle meets line BC, the B-excircle meets line CA, and C-excircle meets line AB, respectively...
. - the incenter coincides with the nine-point center.
- it is equiangular.
- the three altitudeAltitude (triangle)In geometry, an altitude of a triangle is a straight line through a vertex and perpendicular to a line containing the base . This line containing the opposite side is called the extended base of the altitude. The intersection between the extended base and the altitude is called the foot of the...
s have equal lengths. - the three medianMedian (geometry)In geometry, a median of a triangle is a line segment joining a vertex to the midpoint of the opposing side. Every triangle has exactly three medians; one running from each vertex to the opposite side...
s have equal lengths. - the three angle bisectors have equal lengths.
- the three exradii are equal.
Assuming the lengths of the sides of the equilateral triangle are
 , we can determine using the Pythagorean theorem
, we can determine using the Pythagorean theoremPythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
that:
- The area is

- The perimeter is
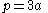
- The radius of the circumscribed circleCircumscribed circleIn geometry, the circumscribed circle or circumcircle of a polygon is a circle which passes through all the vertices of the polygon. The center of this circle is called the circumcenter....
is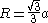
- The radius of the inscribed circle is

- The geometric center of the triangle is the center of the circumscribed and inscribed circles
- And the altitudeAltitude (triangle)In geometry, an altitude of a triangle is a straight line through a vertex and perpendicular to a line containing the base . This line containing the opposite side is called the extended base of the altitude. The intersection between the extended base and the altitude is called the foot of the...
(height) from any side is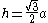 .
.
By Euler's inequality
Euler's theorem in geometry
In geometry, Euler's theorem, named after Leonhard Euler, states that the distance d between the circumcentre and incentre of a triangle can be expressed as d^2=R \,...
, the equilateral triangle has the smallest ratio R/r of the circumradius to the inradius of any triangle: specifically, R/r =2.
The ratio of the area to the square of the perimeter of an equilateral triangle,
 is larger than that for any other triangle.
is larger than that for any other triangle.For any point P in the plane, with distances p, q, and t from the vertices A, B, and C respectively,
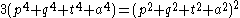 .
.For any interior point P in an equilateral triangle, with distances d, e, and f from the sides, d+e+f = the altitude of the triangle, independent of the location of P.
For any point P on the inscribed circle of an equilateral triangle, with distances p, q, and t from the vertices,
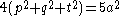
and
 .
.For any point P on the minor arc BC of the circumcircle, with distances p, q, and t from A, B, and C respectively,
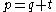
and
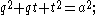
moreover, if point D on side BC divides PA into segments PD and DA with DA having length z and PD having length y, then
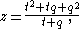
which also equals
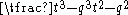 if t ≠ q; and
if t ≠ q; and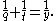
The triangle of largest area of all those inscribed in a given circle is equilateral; and the triangle of smallest area of all those circumscribed around a given circle is equilateral.

