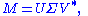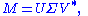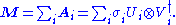Singular value decomposition
Encyclopedia
In linear algebra
, the singular value decomposition (SVD) is a factorization
of a real
or complex
matrix
, with many useful applications in signal processing
and statistics
.
Formally, the singular value decomposition of an m×n real or complex matrix M is a factorization of the form
where U is an m×m real or complex unitary matrix, Σ is an m×n rectangular diagonal matrix with nonnegative real numbers on the diagonal, and V* (the conjugate transpose
of V) is an n×n real or complex unitary matrix. The diagonal entries Σi,i of Σ are known as the singular values of M. The m columns of U and the n columns of V are called the left singular vectors and right singular vectors of M, respectively.
The singular value decomposition and the eigendecomposition are closely related. Namely:
Applications which employ the SVD include computing the pseudoinverse, least squares
fitting of data, matrix approximation, and determining the rank, range and null space of a matrix.
whose entries come from the field
K, which is either the field of real number
s or the field of complex number
s. Then there exists a factorization of the form
where U is an m×m unitary matrix over K, the matrix Σ is an m×n diagonal matrix
with nonnegative real numbers on the diagonal, and V*, an n×n unitary matrix over K, denotes the conjugate transpose
of V. Such a factorization is called the singular value decomposition of M.
The diagonal entries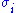
of Σ are known as the singular values of M. A common convention is to list the singular values in descending order. In this case, the diagonal matrix Σ is uniquely determined by M (though the matrices U and V are not).
whose entries are plain real number
s, then U, V*, and Σ are m×m matrices of real numbers as well, Σ can be regarded as a scaling matrix, and U and V* can be viewed as rotation matrices.
If the above mentioned conditions are met, the expression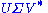
can thus be intuitively interpreted as a composition
(or sequence
) of three geometrical transformations: a rotation, a scaling
, and another rotation. For instance, the figure above explains how a shear matrix
can be described as such a sequence.
in 2-D. This concept can be generalized to n-dimensional Euclidean space
, with the singular values of any n×n square matrix being viewed as the semiaxes of an n-dimensional ellipsoid. See below for further details.
.
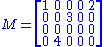
A singular value decomposition of this matrix is given by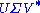
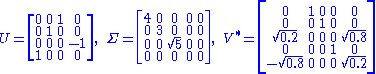
Notice
contains only zeros outside of the diagonal. Furthermore, because the matrices 
and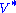 
are unitary, multiplying by their respective conjugate transposes yields identity matrices
, as shown below. In this case, because
and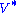 
are real valued, they each are an orthogonal matrix
.
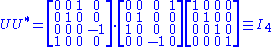
and
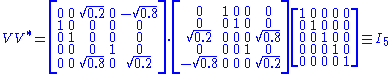
It should also be noted that this particular singular value decomposition is not unique. Choosing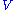
such that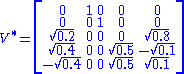
is also a valid singular value decomposition.
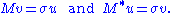
The vectors u and v are called left-singular and right-singular vectors for σ, respectively.
In any singular value decomposition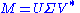
the diagonal entries of Σ are equal to the singular values of M. The columns of U and V are, respectively, left- and right-singular vectors for the corresponding singular values. Consequently, the above theorem implies that:
A singular value for which we can find two left (or right) singular vectors that are linearly dependent is called degenerate.
Non-degenerate singular values always have unique left and right singular vectors, up to multiplication by a unit phase factor eiφ (for the real case up to sign). Consequently, if all singular values of M are non-degenerate and non-zero, then its singular value decomposition is unique, up to multiplication of a column of U by a unit phase factor and simultaneous multiplication of the corresponding column of V by the same unit phase factor.
Degenerate singular values, by definition, have non-unique singular vectors. Furthermore, if u1 and u2 are two left-singular vectors which both correspond to the singular value σ, then any normalized linear combination of the two vectors is also a left singular vector corresponding to the singular value σ. The similar statement is true for right singular vectors. Consequently, if M has degenerate singular values, then its singular value decomposition is not unique.
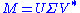is
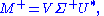
where Σ+ is the pseudoinverse of Σ, which is formed by replacing every nonzero diagonal entry by its reciprocal
and transposing the resulting matrix. The pseudoinverse is one way to solve linear least squares
problems.
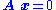for a matrix 
and vector 
. A typical situation is that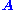 
is known and a non-zero 
is to be determined which satisfies the equation. Such an 
belongs to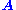
's null space and is sometimes called a (right) null vector of
. 
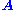can be characterized as a right singular vector corresponding
to a singular value of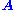
that is zero. This observation means that if 
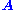is a square matrix and has no vanishing singular value, the equation has no non-zero 
as a solution. It also means that if there are several vanishing singular values, any linear combination of the corresponding right singular vectors is a valid solution. Analogously
to the definition of a (right) null vector, a non-zero
satisfying
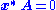, with 
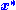denoting the conjugate transpose of
, is called a left null vector of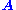 
.
which minimizes the 2-norm of a vector 
under the constraint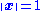 
. The solution turns out to be the right singular vector of 
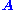corresponding to the smallest singular value.
and null space
of a matrix M. The right singular vectors corresponding to vanishing singular values of M span the null space of M. E.g., the null space is spanned by the last two columns of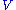
in the above example. The left singular vectors corresponding to the non-zero singular values of M span the range of M. As a consequence, the rank of M equals the number of non-zero singular values which is the same as the number of non-zero diagonal elements in 
.
In numerical linear algebra the singular values can be used to determine the effective rank of a matrix, as rounding error may lead to small but non-zero singular values in a rank deficient matrix.
with another matrix 
which has a specific rank 
. In the case that the approximation is based on minimizing the Frobenius norm of the difference between 
and 
under the constraint that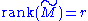 
it turns out that the solution is given by the SVD of 
, namely
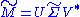
where
is the same matrix as 
except that it contains only the 
largest singular values (the other singular values are replaced by zero). This is known as the Eckart–Young theorem, as it was proved by those two authors in 1936 (although it was later found to have been known to earlier authors; see ).
Quick proof: We hope to minimize
subject to 
.
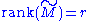Suppose the SVD of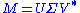
. Since the Frobenius norm is unitarily invariant, we have an equivalent statement: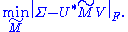
Note that since
is diagonal, 
should be diagonal in order to minimize the Frobenius norm. Remember that the Frobenius norm is the square-root of the summation of the squared modulus of all entries.
This implies that
and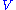 
are also singular matrices of 
. Thus we can assume that 
to minimize the above statement has the form: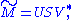
where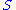
is diagonal. The diagonal entries 
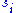of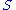 
are not necessarily ordered as in SVD.
From the rank constraint, i.e.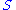
has 
non-zero diagonal entries, the minimum of the above statement is obtained as follows: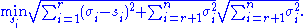
Therefore,
of rank 
is the best approximation of 
in the Frobenius norm sense when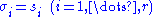 
and the corresponding singular vectors are same as those of 
.
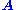can be written as an outer product
of two vectors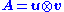
, or, in coordinates, 
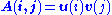. Specifically, the matrix M can be decomposed as:
Here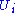
and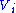 
are the ith columns of the corresponding SVD matrices, 
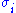are the ordered singular values, and each 
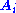is separable. The SVD can be used to find the decomposition of an image processing filter into separable horizontal and vertical filters. Note that the number of non-zero 
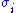is exactly the rank of the matrix.
Separable models often arise in biological systems, and the SVD decomposition is useful to analyze such systems. For example, some visual area V1 simple cells receptive fields can be well described by a Gabor filter
in the space domain multiplied by a modulation function in the time domain. Thus, given a linear filter evaluated through, for example, reverse correlation, one can rearrange the two spatial dimensions into one dimension, thus yielding a two dimensional filter (space, time) which can be decomposed through SVD. The first column of U in the SVD decomposition is then a Gabor while the first column of V represents the time modulation (or vice-versa). One may then define an index of separability,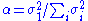
, which is the fraction of the power in the matrix M which is accounted for by the first separable matrix in the decomposition.
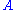to determine the orthogonal matrix
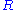closest to 
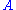. The closeness of fit is measured by the Frobenius norm of 
. The solution is the product 
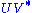. This intuitively makes sense because an orthogonal matrix would have the decomposition 
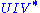where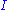 
is the identity matrix, so that if 
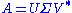then the product 
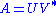amounts to replacing the singular values with ones.
A similar problem, with interesting applications in shape analysis
, is the orthogonal Procrustes problem
, which consists of finding an orthogonal matrix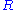
which most closely maps 
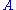to 
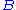. Specifically,
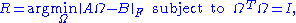
where
denotes the Frobenius norm.
This problem is equivalent to finding the nearest orthogonal matrix to a given matrix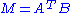
.
(called Wahba's problem
in other fields) uses SVD to compute the optimal rotation (with respect to least-squares minimization) that will align a set of points with a corresponding set of points. It is used, among other applications, to compare the structures of molecules.
s, and is useful in the analysis of regularization methods such as that of Tikhonov
. It is widely used in statistics
where it is related to principal component analysis and to Correspondence analysis
, and in signal processing
and pattern recognition
. It is also used in output-only modal analysis
, where the non-scaled mode shapes can be determined from the singular vectors. Yet another usage is latent semantic indexing
in natural language text processing.
The SVD also plays a crucial role in the field of Quantum information
, in a form often referred to as the Schmidt decomposition
. Through it, states of two quantum systems are naturally decomposed, providing a necessary and sufficient condition for them to be entangled : if the rank of the
matrix is larger than one.
One application of SVD to rather large matrices is in numerical weather prediction
, where Lanczos method
s are used to estimate the most linearly quickly growing few perturbations to the central numerical weather prediction over a given initial forward time period — i.e. the singular vectors corresponding to the largest singular values of the linearized propagator for the global weather over that time interval. The output singular vectors in this case are entire weather systems. These perturbations are then run through the full nonlinear model to generate an ensemble forecast
, giving a handle on some of the uncertainty that should be allowed for around the current central prediction.
Another application of SVD for daily life is that point in perspective view can be unprojected in a photo using the calculated SVD matrix, this application leads to measuring length (a.k.a. the distance of two unprojected points in perspective photo) by marking out the 4 corner points of known-size object in a single photo. PRuler is a demo to implement this application by taking a photo of a regular credit card
Given an SVD of M, as described above, the following two relations hold:
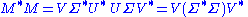
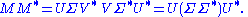
The right hand sides of these relations describe the eigenvalue decompositions of the left hand sides. Consequently:
In the special case that M is a normal matrix
, which by definition must be square, the spectral theorem says that it can be unitarily diagonalized
using a basis of eigenvectors, so that it can be written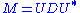
for a unitary matrix U and a diagonal matrix D. When M is also positive semi-definite
, the decomposition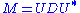
is also a singular value decomposition.
However, the eigenvalue decomposition and the singular value decomposition differ for all other matrices M: the eigenvalue decomposition is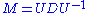
where U is not necessarily unitary and D is not necessarily positive semi-definite, while the SVD is 
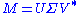where Σ is a diagonal positive semi-definite, and U and V are unitary matrices that are not necessarily related except through the matrix M.
, this continuous function attains a maximum at some u when restricted to the closed unit sphere {||x|| ≤ 1}. By the Lagrange multipliers
theorem, u necessarily satisfies
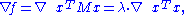
where the nabla symbol,
, is the del
operator.
A short calculation shows the above leads to M u = λ u (symmetry of M is needed here). Therefore λ is the largest eigenvalue of M. The same calculation performed on the orthogonal complement of u gives the next largest eigenvalue and so on. The complex Hermitian case is similar; there f(x) = x* M x is a real-valued function of 2n real variables.
Singular values are similar in that they can be described algebraically or from variational principles. Although, unlike the eigenvalue case, Hermiticity, or symmetry, of M is no longer required.
This section gives these two arguments for existence of singular value decomposition.
, there exists a unitary n-by-n matrix V such that
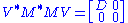
where D is diagonal and positive definite. Partition V appropriately so we can write
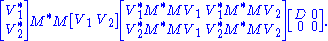
Therefore V1*M*MV1 = D and V2*M*MV2 = 0. The latter means MV2 = 0.
Also, since V is unitary, V1*V1 = I, V2*V2 = I and V1V1* + V2V2* = I.
Define
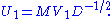
Then
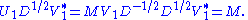
We see that this is almost the desired result, except that U1 and V1 are not unitary in general, but merely isometries
. To finish the argument, one simply has to "fill out" these matrices to obtain unitaries. For example, one can choose U2 such that
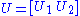
is unitary.
Define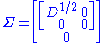
where extra zero rows are added or removed to make the number of zero rows equal the number of columns of U2. Then
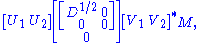
which is the desired result: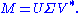
Notice the argument could begin with diagonalizing MM* rather than M*M (This shows directly that MM* and M*M have the same non-zero eigenvalues).
Let M denote an m × n matrix with real entries. Let
and 
denote the sets of unit 2-norm vectors in Rm and Rn respectively. Define the function
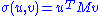
for vectors u ∈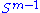
and v ∈ 
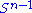. Consider the function σ restricted to 
× 
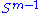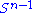. Since both 
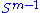and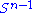 
are compact
sets, their product
is also compact. Furthermore, since σ is continuous, it attains a largest value for at least one pair of vectors u ∈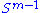
and v ∈ 
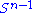. This largest value is denoted σ1 and the corresponding vectors are denoted u1 and v1. Since 
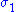is the largest value of 
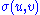it must be non-negative. If it were negative, changing the sign of either u1 or v1 would make it positive and therefore larger.
Statement: u1, v1 are left and right singular vectors of M with corresponding singular value σ1.
Proof: Similar to the eigenvalues case, by assumption the two vectors satisfy the Lagrange multiplier equation:
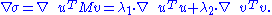
After some algebra, this becomes
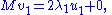
and
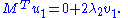
Multiplying the first equation from left by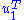
and the second equation from left by 
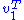and taking ||u|| = ||v|| = 1 into account gives
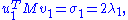
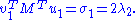
So σ1 = 2 λ1 = 2 λ2. By properties of the functional φ defined by
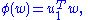
we have
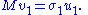
Similarly,
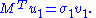
This proves the statement.
More singular vectors and singular values can be found by maximizing σ(u, v) over normalized u, v which are orthogonal to u1 and v1, respectively.
The passage from real to complex is similar to the eigenvalue case.
of Km and the columns v1,...,vn
of V yield an orthonormal basis of Kn (with respect to the standard scalar products on these spaces).
The linear transformation
T :Kn → Km that takes a vector x to Mx has a particularly simple description with respect to these orthonormal bases: we have T(vi) = σi ui, for i = 1,...,min(m,n), where σi is the i-th diagonal entry of Σ, and T(vi) = 0 for i > min(m,n).
The geometric content of the SVD theorem can thus be summarized as follows: for every linear map T :Kn → Km one can find orthonormal bases of Kn and Km such that T maps the i-th basis vector of Kn to a non-negative multiple of the i-th basis vector of Km, and sends the left-over basis vectors to zero.
With respect to these bases, the map T is therefore represented by a diagonal matrix with non-negative real diagonal entries.
To get a more visual flavour of singular values and SVD decomposition —at least when working on real vector spaces— consider the sphere S of radius one in Rn. The linear map T maps this sphere onto an ellipsoid in Rm. Non-zero singular values are simply the lengths of the semi-axes
of this ellipsoid. Especially when n=m, and all the singular values are distinct and non-zero, the SVD of the linear map T can be easily analysed as a succession of three consecutive moves : consider the ellipsoid T(S) and specifically its axes ; then consider the directions in Rn sent by T onto these axes. These directions happen to be mutually orthogonal. Apply first an isometry v* sending these directions to the coordinate axes of Rn. On a second move, apply an endomorphism
d diagonalized along the coordinate axes and stretching or shrinking in each direction, using the semi-axes lengths of T(S) as stretching coefficients. The composition d o v* then sends the unit-sphere onto an ellipsoid isometric to T(S). To define the third and last move u, just apply an isometry to this ellipsoid so as to carry it over T(S). As can be easily checked, the composition u o d o v* coincides with T.
. This takes O(mn2) floating-point operations, assuming that m ≥ n (this formulation uses the big O notation
). The second step is to compute the SVD of the bidiagonal matrix. This step can only be done with an iterative method
(as with eigenvalue algorithm
s). However, in practice it suffices to compute the SVD up to a certain precision, like the machine epsilon
. If this precision is considered constant, then the second step takes O(n) iterations, each costing O(n) flops. Thus, the first step is more expensive, and the overall cost is O(mn2) flops .
The first step can be done using Householder reflections for a cost of 4mn2 − 4n3/3 flops, assuming that only the singular values are needed and not the singular vectors. If m is much larger than n then it is advantageous to first reduce the matrix M to a triangular matrix with the QR decomposition
and then use Householder reflections to further reduce the matrix to bidiagonal form; the combined cost is 2mn2 + 2n3 flops .
The second step can be done by a variant of the QR algorithm
for the computation of eigenvalues, which was first described by . The LAPACK
subroutine DBDSQR implements this iterative method, with some modifications to cover the case where the singular values are very small . Together with a first step using Householder reflections and, if appropriate, QR decomposition, this forms the DGESVD routine for the computation of the singular value decomposition.
The same algorithm is implemented in the GNU Scientific Library
(GSL). The GSL also offers an alternative method, which uses a one-sided Jacobi orthogonalization in step 2 . This method computes the SVD of the bidiagonal matrix by solving a sequence of 2-by-2 SVD problems, similar to how the Jacobi eigenvalue algorithm
solves a sequence of 2-by-2 eigenvalue methods . Yet another method for step 2 uses the idea of divide-and-conquer eigenvalue algorithm
s .
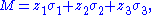
where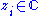
are complex numbers that parameterize the matrix, and 
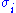denote the Pauli matrices
. Then its two singular values are given by
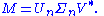
Only the n column vectors of U corresponding to the row vectors of V* are calculated. The remaining column vectors of U are not calculated. This is significantly quicker and more economical than the full SVD if n<n is thus m×n, Σn is n×n diagonal, and V is n×n.
The first stage in the calculation of a thin SVD will usually be a QR decomposition
of M, which can make for a significantly quicker calculation if n<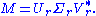
Only the r column vectors of U and r row vectors of V* corresponding to the non-zero singular values Σr are calculated. The remaining vectors of U and V* are not calculated. This is quicker and more economical than the thin SVD if r<r is thus m×r, Σr is r×r diagonal, and Vr* is r×n.
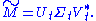
Only the t column vectors of U and t row vectors of V* corresponding to the t largest singular values Σt are calculated. The rest of the matrix is discarded. This can be much quicker and more economical than the compact SVD if t<t is thus m×t, Σt is t×t diagonal, and Vt* is t×n'.
Of course the truncated SVD is no longer an exact decomposition of the original matrix M, but as discussed below, the approximate matrix
is in a very useful sense the closest approximation to M that can be achieved by a matrix of rank t.
k-norm of M.
The first of the Ky Fan norms, the Ky Fan 1-norm is the same as the operator norm
of M as a linear operator with respect to the Euclidean norms of Km and Kn. In other words, the Ky Fan 1-norm is the operator norm induced by the standard l2 Euclidean inner product. For this reason, it is also called the operator 2-norm. One can easily verify the relationship between the Ky Fan 1-norm and singular values. It is true in general, for a bounded operator M on (possibly infinite dimensional) Hilbert spaces
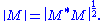
But, in the matrix case, M*M½ is a normal matrix
, so ||M* M||½ is the largest eigenvalue of M* M½, i.e. the largest singular value of M.
The last of the Ky Fan norms, the sum of all singular values, is the trace norm
(also known as the 'nuclear norm'), defined by ||M|| = Tr[(M*M)½] (the diagonal entries of M* M are the squares of the singular values).
. So the induced norm is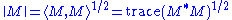 
. Since trace is invariant under unitary equivalence, this shows
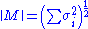
where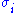
are the singular values of M. This is called the Frobenius norm, Schatten 2-norm, or Hilbert–Schmidt norm of M. Direct calculation shows that if
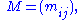
the Frobenius norm of M coincides with
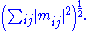
There exist two types of tensor decompositions which generalise SVD to multi-way arrays. One decomposition decomposes a tensor into a sum of rank-1 tensors, see Candecomp-PARAFAC (CP) algorithm. The CP algorithm should not be confused with a rank-R decomposition but, for a given N, it decomposes a tensor into a sum of N rank-1 tensors that optimally fit the original tensor. The second type of decomposition computes the orthonormal subspaces associated with the different axes or modes of a tensor (orthonormal row space, column space, fiber space, etc.). This decomposition is referred to in the literature as the Tucker3/TuckerM
, M-mode SVD, multilinear SVD and sometimes referred to as a higher-order SVD (HOSVD). In addition, multilinear principal component analysis
in multilinear subspace learning
involves the same mathematical operations as Tucker decomposition, being used in a different context of dimensionality reduction
.
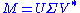can be extended to a bounded operator
M on a separable Hilbert space H. Namely, for any bounded operator M, there exist a partial isometry
U, a unitary V, a measure space (X, μ), and a non-negative measurable f such that
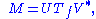
where
is the multiplication by f
on L2(X, μ).
This can be shown by mimicking the linear algebraic argument for the matricial case above. VTf V* is the unique positive square root of M*M, as given by the Borel functional calculus
for self adjoint operators. The reason why U need not be unitary is because, unlike the finite dimensional case, given an isometry U1 with non trivial kernel, a suitable U2 may not be found such that
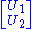
is a unitary operator.
As for matrices, the singular value factorization is equivalent to the polar decomposition for operators: we can simply write
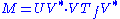
and notice that U V* is still a partial isometry while VTf V* is positive.
. It is a general fact that compact operators on Banach space
s have only discrete spectrum. This is also true for compact operators on Hilbert spaces, since Hilbert space
s are a special case of Banach spaces. If T is compact, every nonzero λ in its spectrum is an eigenvalue. Furthermore, a compact self adjoint operator can be diagonalized by its eigenvectors. If M is compact, so is M*M. Applying the diagonalization result, the unitary image of its positive square root Tf has a set of orthonormal eigenvectors {ei} corresponding to strictly positive eigenvalues {σi}. For any ψ ∈ H,
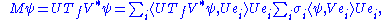
where the series converges in the norm topology on H. Notice how this resembles the expression from the finite dimensional case. The σi 's are called the singular values of M. {U ei} and {V ei} can be considered the left- and right-singular vectors of M respectively.
Compact operators on a Hilbert space
are the closure of finite-rank operators in the uniform operator topology. The above series expression gives an explicit such representation. An immediate consequence of this is:
Theorem M is compact if and only if M*M is compact.
and Camille Jordan
discovered independently, in 1873 and 1874 respectively, that the singular values of the bilinear forms, represented as a matrix, form a complete set
of invariant
s for bilinear forms under orthogonal substitutions. James Joseph Sylvester
also arrived at the singular value decomposition for real square matrices in 1889, apparently independent of both Beltrami and Jordan. Sylvester called the singular values the canonical multipliers of the matrix A. The fourth mathematician to discover the singular value decomposition independently is Autonne in 1915, who arrived at it via the polar decomposition. The first proof of the singular value decomposition for rectangular and complex matrices seems to be by Carl Eckart
and Gale Young in 1936; they saw it as a generalization of the principal axis transformation for Hermitian matrices.
In 1907, Erhard Schmidt
defined an analog of singular values for integral operators (which are compact, under some weak technical assumptions); it seems he was unaware of the parallel work on singular values of finite matrices. This theory was further developed by Émile Picard in 1910, who is the first to call the numbers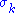
singular values (or rather, valeurs singulières).
Practical methods for computing the SVD date back to Kogbetliantz
in 1954, 1955 and Hestenes
in 1958. resembling closely the Jacobi eigenvalue algorithm
, which uses plane rotations or Givens rotations. However, these were replaced by the method of Gene Golub
and William Kahan
published in 1965, which uses Householder transformation
s or reflections.
In 1970, Golub and Christian Reinsch published a variant of the Golub/Kahan algorithm that is still the one most-used today.
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, the singular value decomposition (SVD) is a factorization
Matrix decomposition
In the mathematical discipline of linear algebra, a matrix decomposition is a factorization of a matrix into some canonical form. There are many different matrix decompositions; each finds use among a particular class of problems.- Example :...
of a real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
or complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
, with many useful applications in signal processing
Signal processing
Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
.
Formally, the singular value decomposition of an m×n real or complex matrix M is a factorization of the form
where U is an m×m real or complex unitary matrix, Σ is an m×n rectangular diagonal matrix with nonnegative real numbers on the diagonal, and V* (the conjugate transpose
Conjugate transpose
In mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...
of V) is an n×n real or complex unitary matrix. The diagonal entries Σi,i of Σ are known as the singular values of M. The m columns of U and the n columns of V are called the left singular vectors and right singular vectors of M, respectively.
The singular value decomposition and the eigendecomposition are closely related. Namely:
- The left singular vectors of M are eigenvectors of
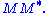
- The right singular vectors of M are eigenvectors of
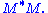
- The non-zero singular values of M (found on the diagonal entries of Σ) are the square roots of the non-zero eigenvalues of
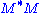or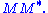 
Applications which employ the SVD include computing the pseudoinverse, least squares
Least squares
The method of least squares is a standard approach to the approximate solution of overdetermined systems, i.e., sets of equations in which there are more equations than unknowns. "Least squares" means that the overall solution minimizes the sum of the squares of the errors made in solving every...
fitting of data, matrix approximation, and determining the rank, range and null space of a matrix.
Statement of the theorem
Suppose M is an m×n matrixMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
whose entries come from the field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
K, which is either the field of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s or the field of complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s. Then there exists a factorization of the form
where U is an m×m unitary matrix over K, the matrix Σ is an m×n diagonal matrix
Diagonal matrix
In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
with nonnegative real numbers on the diagonal, and V*, an n×n unitary matrix over K, denotes the conjugate transpose
Conjugate transpose
In mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...
of V. Such a factorization is called the singular value decomposition of M.
The diagonal entries
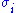of Σ are known as the singular values of M. A common convention is to list the singular values in descending order. In this case, the diagonal matrix Σ is uniquely determined by M (though the matrices U and V are not).Rotation, scaling, rotation
In the special but common case in which M is just an m×m square matrix with positive determinantDeterminant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
whose entries are plain real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, then U, V*, and Σ are m×m matrices of real numbers as well, Σ can be regarded as a scaling matrix, and U and V* can be viewed as rotation matrices.
If the above mentioned conditions are met, the expression
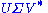can thus be intuitively interpreted as a compositionFunction composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
(or sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
) of three geometrical transformations: a rotation, a scaling
Scaling (geometry)
In Euclidean geometry, uniform scaling is a linear transformation that enlarges or shrinks objects by a scale factor that is the same in all directions. The result of uniform scaling is similar to the original...
, and another rotation. For instance, the figure above explains how a shear matrix
Shear matrix
In mathematics, a shear matrix or transvection is an elementary matrix that represents the addition of a multiple of one row or column to another...
can be described as such a sequence.
Singular values as semiaxis of an ellipse or ellipsoid
As shown in the figure, the singular values can be interpreted as the semiaxes of an ellipseEllipse
In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
in 2-D. This concept can be generalized to n-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
, with the singular values of any n×n square matrix being viewed as the semiaxes of an n-dimensional ellipsoid. See below for further details.
U and V are orthonormal bases
Since U and V* are unitary, the columns of each of them form a set of orthonormal vectors, which can be regarded as basis vectors. By the definition of unitary matrix, the same is true for their conjugate transposes U* and V. In short, U, U*, V, and V* are orthonormal basesOrthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
.
Example
Consider the 4×5 matrix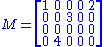A singular value decomposition of this matrix is given by
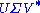
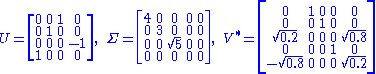
Notice
contains only zeros outside of the diagonal. Furthermore, because the matrices and 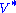are unitary, multiplying by their respective conjugate transposes yields identity matricesIdentity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
, as shown below. In this case, because
and 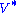are real valued, they each are an orthogonal matrixOrthogonal matrix
In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
.
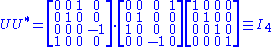
and
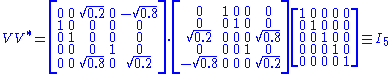
It should also be noted that this particular singular value decomposition is not unique. Choosing
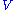such that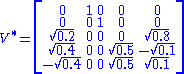is also a valid singular value decomposition.
Singular values, singular vectors, and their relation to the SVD
A non-negative real number σ is a singular value for M if and only if there exist unit-length vectors u in Km and v in Kn such that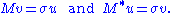The vectors u and v are called left-singular and right-singular vectors for σ, respectively.
In any singular value decomposition
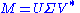
the diagonal entries of Σ are equal to the singular values of M. The columns of U and V are, respectively, left- and right-singular vectors for the corresponding singular values. Consequently, the above theorem implies that:
- An m × n matrix M has at least one and at most p = min(m,n) distinct singular values.
- It is always possible to find an orthogonal basisOrthogonal basisIn mathematics, particularly linear algebra, an orthogonal basis for an inner product space is a basis for whose vectors are mutually orthogonal...
U for Km consisting of left-singular vectors of M.
- It is always possible to find an orthogonal basis V for Kn consisting of right-singular vectors of M.
A singular value for which we can find two left (or right) singular vectors that are linearly dependent is called degenerate.
Non-degenerate singular values always have unique left and right singular vectors, up to multiplication by a unit phase factor eiφ (for the real case up to sign). Consequently, if all singular values of M are non-degenerate and non-zero, then its singular value decomposition is unique, up to multiplication of a column of U by a unit phase factor and simultaneous multiplication of the corresponding column of V by the same unit phase factor.
Degenerate singular values, by definition, have non-unique singular vectors. Furthermore, if u1 and u2 are two left-singular vectors which both correspond to the singular value σ, then any normalized linear combination of the two vectors is also a left singular vector corresponding to the singular value σ. The similar statement is true for right singular vectors. Consequently, if M has degenerate singular values, then its singular value decomposition is not unique.
Pseudoinverse
The singular value decomposition can be used for computing the pseudoinverse of a matrix. Indeed, the pseudoinverse of the matrix M with singular value decomposition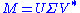 is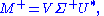where Σ+ is the pseudoinverse of Σ, which is formed by replacing every nonzero diagonal entry by its reciprocal
Multiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
and transposing the resulting matrix. The pseudoinverse is one way to solve linear least squares
Linear least squares
In statistics and mathematics, linear least squares is an approach to fitting a mathematical or statistical model to data in cases where the idealized value provided by the model for any data point is expressed linearly in terms of the unknown parameters of the model...
problems.
Solving homogeneous linear equations
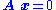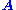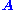A set of homogeneous linear equations can be written as for a matrix and vector . A typical situation is that is known and a non-zero is to be determined which satisfies the equation. Such an belongs to
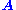's null space and is sometimes called a (right) null vector of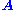. can be characterized as a right singular vector correspondingto a singular value of
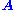that is zero. This observation means that if 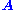is a square matrix and has no vanishing singular value, the equation has no non-zero as a solution. It also means that if there are several vanishing singular values, any linear combination of the corresponding right singular vectors is a valid solution. Analogouslyto the definition of a (right) null vector, a non-zero
satisfying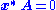, with 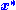denoting the conjugate transpose of, is called a left null vector of 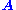.Total least squares minimization
A total least squares problem refers to determining the vector which minimizes the 2-norm of a vector under the constraint 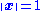. The solution turns out to be the right singular vector of 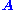corresponding to the smallest singular value.Range, null space and rank
Another application of the SVD is that it provides an explicit representation of the rangeColumn space
In linear algebra, the column space of a matrix is the set of all possible linear combinations of its column vectors. The column space of an m × n matrix is a subspace of m-dimensional Euclidean space...
and null space
Null space
In linear algebra, the kernel or null space of a matrix A is the set of all vectors x for which Ax = 0. The kernel of a matrix with n columns is a linear subspace of n-dimensional Euclidean space...
of a matrix M. The right singular vectors corresponding to vanishing singular values of M span the null space of M. E.g., the null space is spanned by the last two columns of
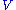in the above example. The left singular vectors corresponding to the non-zero singular values of M span the range of M. As a consequence, the rank of M equals the number of non-zero singular values which is the same as the number of non-zero diagonal elements in .In numerical linear algebra the singular values can be used to determine the effective rank of a matrix, as rounding error may lead to small but non-zero singular values in a rank deficient matrix.
Low-rank matrix approximation
Some practical applications need to solve the problem of approximating a matrix with another matrix which has a specific rank . In the case that the approximation is based on minimizing the Frobenius norm of the difference between and under the constraint that 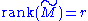it turns out that the solution is given by the SVD of , namely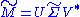where
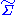is the same matrix as except that it contains only the largest singular values (the other singular values are replaced by zero). This is known as the Eckart–Young theorem, as it was proved by those two authors in 1936 (although it was later found to have been known to earlier authors; see ).Quick proof: We hope to minimize
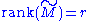subject to .Suppose the SVD of
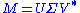. Since the Frobenius norm is unitarily invariant, we have an equivalent statement: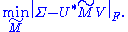Note that since
is diagonal, should be diagonal in order to minimize the Frobenius norm. Remember that the Frobenius norm is the square-root of the summation of the squared modulus of all entries.This implies that
and 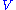are also singular matrices of . Thus we can assume that to minimize the above statement has the form: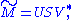where
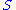is diagonal. The diagonal entries 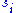of 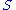are not necessarily ordered as in SVD.From the rank constraint, i.e.
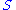has non-zero diagonal entries, the minimum of the above statement is obtained as follows: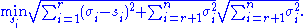Therefore,
of rank is the best approximation of in the Frobenius norm sense when 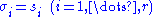and the corresponding singular vectors are same as those of .Separable models
The SVD can be thought of as decomposing a matrix into a weighted, ordered sum of separable matrices. By separable, we mean that a matrix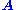 can be written as an outer productOuter product
In linear algebra, the outer product typically refers to the tensor product of two vectors. The result of applying the outer product to a pair of vectors is a matrix...
of two vectors
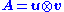, or, in coordinates, 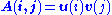. Specifically, the matrix M can be decomposed as:
Here
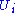and 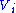are the ith columns of the corresponding SVD matrices, 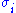are the ordered singular values, and each 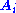is separable. The SVD can be used to find the decomposition of an image processing filter into separable horizontal and vertical filters. Note that the number of non-zero 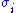is exactly the rank of the matrix.Separable models often arise in biological systems, and the SVD decomposition is useful to analyze such systems. For example, some visual area V1 simple cells receptive fields can be well described by a Gabor filter
Gabor filter
In image processing, a Gabor filter, named after Dennis Gabor, is a linear filter used for edge detection. Frequency and orientation representations of Gabor filters are similar to those of the human visual system, and they have been found to be particularly appropriate for texture representation...
in the space domain multiplied by a modulation function in the time domain. Thus, given a linear filter evaluated through, for example, reverse correlation, one can rearrange the two spatial dimensions into one dimension, thus yielding a two dimensional filter (space, time) which can be decomposed through SVD. The first column of U in the SVD decomposition is then a Gabor while the first column of V represents the time modulation (or vice-versa). One may then define an index of separability,
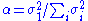, which is the fraction of the power in the matrix M which is accounted for by the first separable matrix in the decomposition.Nearest orthogonal matrix
It is possible to use the SVD of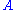 to determine the orthogonal matrixOrthogonal matrix
In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
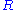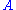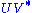closest to . The closeness of fit is measured by the Frobenius norm of . The solution is the product . This intuitively makes sense because an orthogonal matrix would have the decomposition 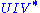where 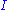is the identity matrix, so that if 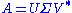then the product 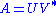amounts to replacing the singular values with ones.A similar problem, with interesting applications in shape analysis
Shape analysis
This article describes shape analysis to analyze and process geometric shapes.The shape analysis described here is related to the statistical analysis of geometric shapes, to shape matching and shape recognition...
, is the orthogonal Procrustes problem
Orthogonal Procrustes problem
The orthogonal Procrustes problem is a matrix approximation problem in linear algebra. In its classical form, one is given two matrices A and B and asked to find an orthogonal matrix R which most closely maps A to B...
, which consists of finding an orthogonal matrix
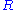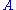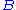which most closely maps to . Specifically,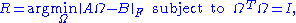where
denotes the Frobenius norm.This problem is equivalent to finding the nearest orthogonal matrix to a given matrix
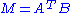.The Kabsch Algorithm
The Kabsch algorithmKabsch algorithm
The Kabsch algorithm, named after Wolfgang Kabsch, is a method for calculating the optimal rotation matrix that minimizes the RMSD between two paired sets of points...
(called Wahba's problem
Wahba's problem
In applied mathematics, Wahba's problem, first posed by Grace Wahba in 1965, seeks to find a rotation matrix between two coordinate systems from a set of vector observations. Solutions to Wahba's problem are often used in satellite attitude determination utilising sensors such as magnetometers...
in other fields) uses SVD to compute the optimal rotation (with respect to least-squares minimization) that will align a set of points with a corresponding set of points. It is used, among other applications, to compare the structures of molecules.
Other examples
The SVD is also applied extensively to the study of linear inverse problemInverse problem
An inverse problem is a general framework that is used to convert observed measurements into information about a physical object or system that we are interested in...
s, and is useful in the analysis of regularization methods such as that of Tikhonov
Tikhonov regularization
Tikhonov regularization, named for Andrey Tikhonov, is the most commonly used method of regularization of ill-posed problems. In statistics, the method is known as ridge regression, and, with multiple independent discoveries, it is also variously known as the Tikhonov-Miller method, the...
. It is widely used in statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
where it is related to principal component analysis and to Correspondence analysis
Correspondence analysis
Correspondence analysis is a multivariate statistical technique proposed by Hirschfeld and later developed by Jean-Paul Benzécri. It is conceptually similar to principal component analysis, but applies to categorical rather than continuous data...
, and in signal processing
Signal processing
Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
and pattern recognition
Pattern recognition
In machine learning, pattern recognition is the assignment of some sort of output value to a given input value , according to some specific algorithm. An example of pattern recognition is classification, which attempts to assign each input value to one of a given set of classes...
. It is also used in output-only modal analysis
Modal analysis
Modal analysis is the study of the dynamic properties of structures under vibrational excitation.Modal analysis is the field of measuring and analysing the dynamic response of structures and or fluids when excited by an input...
, where the non-scaled mode shapes can be determined from the singular vectors. Yet another usage is latent semantic indexing
Latent semantic indexing
Latent Semantic Indexing is an indexing and retrieval method that uses a mathematical technique called Singular value decomposition to identify patterns in the relationships between the terms and concepts contained in an unstructured collection of text. LSI is based on the principle that words...
in natural language text processing.
The SVD also plays a crucial role in the field of Quantum information
Quantum information
In quantum mechanics, quantum information is physical information that is held in the "state" of a quantum system. The most popular unit of quantum information is the qubit, a two-level quantum system...
, in a form often referred to as the Schmidt decomposition
Schmidt decomposition
In linear algebra, the Schmidt decomposition refers to a particular way of expressing a vector in the tensor product of two inner product spaces. It has applications in quantum information theory and plasticity....
. Through it, states of two quantum systems are naturally decomposed, providing a necessary and sufficient condition for them to be entangled : if the rank of the
matrix is larger than one.One application of SVD to rather large matrices is in numerical weather prediction
Numerical weather prediction
Numerical weather prediction uses mathematical models of the atmosphere and oceans to predict the weather based on current weather conditions. Though first attempted in the 1920s, it was not until the advent of computer simulation in the 1950s that numerical weather predictions produced realistic...
, where Lanczos method
Lanczos algorithm
The Lanczos algorithm is an iterative algorithm invented by Cornelius Lanczos that is an adaptation of power methods to find eigenvalues and eigenvectors of a square matrix or the singular value decomposition of a rectangular matrix. It is particularly useful for finding decompositions of very...
s are used to estimate the most linearly quickly growing few perturbations to the central numerical weather prediction over a given initial forward time period — i.e. the singular vectors corresponding to the largest singular values of the linearized propagator for the global weather over that time interval. The output singular vectors in this case are entire weather systems. These perturbations are then run through the full nonlinear model to generate an ensemble forecast
Ensemble forecasting
Ensemble forecasting is a numerical prediction method that is used to attempt to generate a representative sample of the possible future states of a dynamical system...
, giving a handle on some of the uncertainty that should be allowed for around the current central prediction.
Another application of SVD for daily life is that point in perspective view can be unprojected in a photo using the calculated SVD matrix, this application leads to measuring length (a.k.a. the distance of two unprojected points in perspective photo) by marking out the 4 corner points of known-size object in a single photo. PRuler is a demo to implement this application by taking a photo of a regular credit card
Relation to eigenvalue decomposition
The singular value decomposition is very general in the sense that it can be applied to any m × n matrix whereas eigenvalue decomposition can only be applied to certain classes of square matrices. Nevertheless, the two decompositions are related.Given an SVD of M, as described above, the following two relations hold:
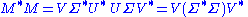
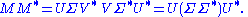
The right hand sides of these relations describe the eigenvalue decompositions of the left hand sides. Consequently:
- The columns of V (right singular vectors) are eigenvectors of
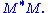
- The columns of U (left singular vectors) are eigenvectors of
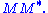
- The non-zero elements of Σ (non-zero singular values) are the square roots of the non-zero eigenvalues of
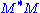or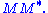 
In the special case that M is a normal matrix
Normal matrix
A complex square matrix A is a normal matrix ifA^*A=AA^* \ where A* is the conjugate transpose of A. That is, a matrix is normal if it commutes with its conjugate transpose.If A is a real matrix, then A*=AT...
, which by definition must be square, the spectral theorem says that it can be unitarily diagonalized
Diagonalizable matrix
In linear algebra, a square matrix A is called diagonalizable if it is similar to a diagonal matrix, i.e., if there exists an invertible matrix P such that P −1AP is a diagonal matrix...
using a basis of eigenvectors, so that it can be written
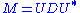for a unitary matrix U and a diagonal matrix D. When M is also positive semi-definitePositive-definite matrix
In linear algebra, a positive-definite matrix is a matrix that in many ways is analogous to a positive real number. The notion is closely related to a positive-definite symmetric bilinear form ....
, the decomposition
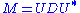is also a singular value decomposition.However, the eigenvalue decomposition and the singular value decomposition differ for all other matrices M: the eigenvalue decomposition is
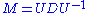where U is not necessarily unitary and D is not necessarily positive semi-definite, while the SVD is 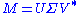where Σ is a diagonal positive semi-definite, and U and V are unitary matrices that are not necessarily related except through the matrix M.Existence
An eigenvalue λ of a matrix is characterized by the algebraic relation M u = λ u. When M is Hermitian, a variational characterization is also available. Let M be a real n × n symmetric matrix. Define f :Rn → R by f(x) = xT M x. By the extreme value theoremExtreme value theorem
In calculus, the extreme value theorem states that if a real-valued function f is continuous in the closed and bounded interval [a,b], then f must attain its maximum and minimum value, each at least once...
, this continuous function attains a maximum at some u when restricted to the closed unit sphere {||x|| ≤ 1}. By the Lagrange multipliers
Lagrange multipliers
In mathematical optimization, the method of Lagrange multipliers provides a strategy for finding the maxima and minima of a function subject to constraints.For instance , consider the optimization problem...
theorem, u necessarily satisfies
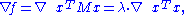
where the nabla symbol,
, is the delDel
In vector calculus, del is a vector differential operator, usually represented by the nabla symbol \nabla . When applied to a function defined on a one-dimensional domain, it denotes its standard derivative as defined in calculus...
operator.
A short calculation shows the above leads to M u = λ u (symmetry of M is needed here). Therefore λ is the largest eigenvalue of M. The same calculation performed on the orthogonal complement of u gives the next largest eigenvalue and so on. The complex Hermitian case is similar; there f(x) = x* M x is a real-valued function of 2n real variables.
Singular values are similar in that they can be described algebraically or from variational principles. Although, unlike the eigenvalue case, Hermiticity, or symmetry, of M is no longer required.
This section gives these two arguments for existence of singular value decomposition.
Based on the spectral theorem
Let M be an m-by-n matrix with complex entries. M*M is positive semidefinite and Hermitian. By the spectral theoremSpectral theorem
In mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized...
, there exists a unitary n-by-n matrix V such that
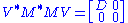
where D is diagonal and positive definite. Partition V appropriately so we can write
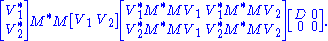
Therefore V1*M*MV1 = D and V2*M*MV2 = 0. The latter means MV2 = 0.
Also, since V is unitary, V1*V1 = I, V2*V2 = I and V1V1* + V2V2* = I.
Define
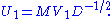
Then
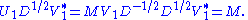
We see that this is almost the desired result, except that U1 and V1 are not unitary in general, but merely isometries
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
. To finish the argument, one simply has to "fill out" these matrices to obtain unitaries. For example, one can choose U2 such that
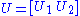
is unitary.
Define
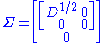
where extra zero rows are added or removed to make the number of zero rows equal the number of columns of U2. Then
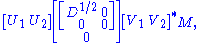
which is the desired result:
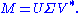
Notice the argument could begin with diagonalizing MM* rather than M*M (This shows directly that MM* and M*M have the same non-zero eigenvalues).
Based on variational characterization
The singular values can also be characterized as the maxima of uTMv, considered as a function of u and v, over particular subspaces. The singular vectors are the values of u and v where these maxima are attained.Let M denote an m × n matrix with real entries. Let
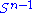and denote the sets of unit 2-norm vectors in Rm and Rn respectively. Define the function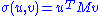for vectors u ∈
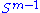and v ∈ 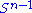. Consider the function σ restricted to 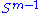× 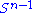. Since both 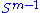and 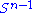are compactCompact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
sets, their product
Product topology
In topology and related areas of mathematics, a product space is the cartesian product of a family of topological spaces equipped with a natural topology called the product topology...
is also compact. Furthermore, since σ is continuous, it attains a largest value for at least one pair of vectors u ∈
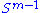and v ∈ 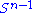. This largest value is denoted σ1 and the corresponding vectors are denoted u1 and v1. Since 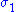is the largest value of 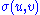it must be non-negative. If it were negative, changing the sign of either u1 or v1 would make it positive and therefore larger.Statement: u1, v1 are left and right singular vectors of M with corresponding singular value σ1.
Proof: Similar to the eigenvalues case, by assumption the two vectors satisfy the Lagrange multiplier equation:
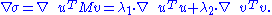
After some algebra, this becomes
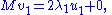
and
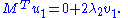
Multiplying the first equation from left by
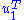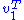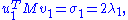
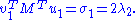
and the second equation from left by and taking ||u|| = ||v|| = 1 into account givesSo σ1 = 2 λ1 = 2 λ2. By properties of the functional φ defined by
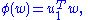
we have
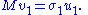
Similarly,
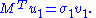
This proves the statement.
More singular vectors and singular values can be found by maximizing σ(u, v) over normalized u, v which are orthogonal to u1 and v1, respectively.
The passage from real to complex is similar to the eigenvalue case.
Geometric meaning
Because U and V are unitary, we know that the columns u1,...,um of U yield an orthonormal basisOrthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
of Km and the columns v1,...,vn
of V yield an orthonormal basis of Kn (with respect to the standard scalar products on these spaces).
The linear transformation
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
T :Kn → Km that takes a vector x to Mx has a particularly simple description with respect to these orthonormal bases: we have T(vi) = σi ui, for i = 1,...,min(m,n), where σi is the i-th diagonal entry of Σ, and T(vi) = 0 for i > min(m,n).
The geometric content of the SVD theorem can thus be summarized as follows: for every linear map T :Kn → Km one can find orthonormal bases of Kn and Km such that T maps the i-th basis vector of Kn to a non-negative multiple of the i-th basis vector of Km, and sends the left-over basis vectors to zero.
With respect to these bases, the map T is therefore represented by a diagonal matrix with non-negative real diagonal entries.
To get a more visual flavour of singular values and SVD decomposition —at least when working on real vector spaces— consider the sphere S of radius one in Rn. The linear map T maps this sphere onto an ellipsoid in Rm. Non-zero singular values are simply the lengths of the semi-axes
Semi-minor axis
In geometry, the semi-minor axis is a line segment associated with most conic sections . One end of the segment is the center of the conic section, and it is at right angles with the semi-major axis...
of this ellipsoid. Especially when n=m, and all the singular values are distinct and non-zero, the SVD of the linear map T can be easily analysed as a succession of three consecutive moves : consider the ellipsoid T(S) and specifically its axes ; then consider the directions in Rn sent by T onto these axes. These directions happen to be mutually orthogonal. Apply first an isometry v* sending these directions to the coordinate axes of Rn. On a second move, apply an endomorphism
Endomorphism
In mathematics, an endomorphism is a morphism from a mathematical object to itself. For example, an endomorphism of a vector space V is a linear map ƒ: V → V, and an endomorphism of a group G is a group homomorphism ƒ: G → G. In general, we can talk about...
d diagonalized along the coordinate axes and stretching or shrinking in each direction, using the semi-axes lengths of T(S) as stretching coefficients. The composition d o v* then sends the unit-sphere onto an ellipsoid isometric to T(S). To define the third and last move u, just apply an isometry to this ellipsoid so as to carry it over T(S). As can be easily checked, the composition u o d o v* coincides with T.
Numerical Approach
The SVD of a matrix M is typically computed by a two-step procedure. In the first step, the matrix is reduced to a bidiagonal matrixBidiagonal matrix
A bidiagonal matrix is a matrix with non-zero entries along the main diagonal and either the diagonal above or the diagonal below.So that means there are two non zero diagonal in the matrix....
. This takes O(mn2) floating-point operations, assuming that m ≥ n (this formulation uses the big O notation
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
). The second step is to compute the SVD of the bidiagonal matrix. This step can only be done with an iterative method
Iterative method
In computational mathematics, an iterative method is a mathematical procedure that generates a sequence of improving approximate solutions for a class of problems. A specific implementation of an iterative method, including the termination criteria, is an algorithm of the iterative method...
(as with eigenvalue algorithm
Eigenvalue algorithm
In linear algebra, one of the most important problems is designing efficient and stable algorithms for finding the eigenvalues of a matrix. These eigenvalue algorithms may also find eigenvectors.-Characteristic polynomial:...
s). However, in practice it suffices to compute the SVD up to a certain precision, like the machine epsilon
Machine epsilon
Machine epsilon gives an upper bound on the relative error due to rounding in floating point arithmetic. This value characterizes computer arithmetic in the field of numerical analysis, and by extension in the subject of computational science...
. If this precision is considered constant, then the second step takes O(n) iterations, each costing O(n) flops. Thus, the first step is more expensive, and the overall cost is O(mn2) flops .
The first step can be done using Householder reflections for a cost of 4mn2 − 4n3/3 flops, assuming that only the singular values are needed and not the singular vectors. If m is much larger than n then it is advantageous to first reduce the matrix M to a triangular matrix with the QR decomposition
QR decomposition
In linear algebra, a QR decomposition of a matrix is a decomposition of a matrix A into a product A=QR of an orthogonal matrix Q and an upper triangular matrix R...
and then use Householder reflections to further reduce the matrix to bidiagonal form; the combined cost is 2mn2 + 2n3 flops .
The second step can be done by a variant of the QR algorithm
QR algorithm
In numerical linear algebra, the QR algorithm is an eigenvalue algorithm: that is, a procedure to calculate the eigenvalues and eigenvectors of a matrix. The QR transformation was developed in the late 1950s by John G.F. Francis and by Vera N. Kublanovskaya , working independently...
for the computation of eigenvalues, which was first described by . The LAPACK
LAPACK
-External links:* : a modern replacement for PLAPACK and ScaLAPACK* on Netlib.org* * * : a modern replacement for LAPACK that is MultiGPU ready* on Sourceforge.net* * optimized LAPACK for Solaris OS on SPARC/x86/x64 and Linux* * *...
subroutine DBDSQR implements this iterative method, with some modifications to cover the case where the singular values are very small . Together with a first step using Householder reflections and, if appropriate, QR decomposition, this forms the DGESVD routine for the computation of the singular value decomposition.
The same algorithm is implemented in the GNU Scientific Library
GNU Scientific Library
In computing, the GNU Scientific Library is a software library written in the C programming language for numerical calculations in applied mathematics and science...
(GSL). The GSL also offers an alternative method, which uses a one-sided Jacobi orthogonalization in step 2 . This method computes the SVD of the bidiagonal matrix by solving a sequence of 2-by-2 SVD problems, similar to how the Jacobi eigenvalue algorithm
Jacobi eigenvalue algorithm
In numerical linear algebra, the Jacobi eigenvalue algorithm is an iterative method for the calculation of the eigenvalues and eigenvectors of a real symmetric matrix...
solves a sequence of 2-by-2 eigenvalue methods . Yet another method for step 2 uses the idea of divide-and-conquer eigenvalue algorithm
Divide-and-conquer eigenvalue algorithm
Divide-and-conquer eigenvalue algorithms are a class of eigenvalue algorithms for Hermitian or real symmetric matrices that have recently become competitive in terms of stability and efficiency with more traditional algorithms such as the QR algorithm. The basic concept behind these algorithms is...
s .
Analytic Result of 2-by-2 SVD
The singular values of a 2-by-2 matrix can be found analytically. Let the matrix be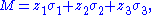where
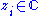are complex numbers that parameterize the matrix, and 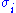denote the Pauli matricesPauli matrices
The Pauli matrices are a set of three 2 × 2 complex matrices which are Hermitian and unitary. Usually indicated by the Greek letter "sigma" , they are occasionally denoted with a "tau" when used in connection with isospin symmetries...
. Then its two singular values are given by
Reduced SVDs
In applications it is quite unusual for the full SVD, including a full unitary decomposition of the null-space of the matrix, to be required. Instead, it is often sufficient (as well as faster, and more economical for storage) to compute a reduced version of the SVD. The following can be distinguished for an m×n matrix M of rank r:Thin SVD
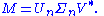
Only the n column vectors of U corresponding to the row vectors of V* are calculated. The remaining column vectors of U are not calculated. This is significantly quicker and more economical than the full SVD if n<
The first stage in the calculation of a thin SVD will usually be a QR decomposition
QR decomposition
In linear algebra, a QR decomposition of a matrix is a decomposition of a matrix A into a product A=QR of an orthogonal matrix Q and an upper triangular matrix R...
of M, which can make for a significantly quicker calculation if n<
Compact SVD
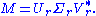
Only the r column vectors of U and r row vectors of V* corresponding to the non-zero singular values Σr are calculated. The remaining vectors of U and V* are not calculated. This is quicker and more economical than the thin SVD if r<
Truncated SVD
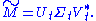
Only the t column vectors of U and t row vectors of V* corresponding to the t largest singular values Σt are calculated. The rest of the matrix is discarded. This can be much quicker and more economical than the compact SVD if t<
Of course the truncated SVD is no longer an exact decomposition of the original matrix M, but as discussed below, the approximate matrix
is in a very useful sense the closest approximation to M that can be achieved by a matrix of rank t.Ky Fan norms
The sum of the k largest singular values of M is a matrix norm, the Ky FanKy Fan
Ky Fan was an American mathematician and Emeritus Professor of Mathematics at the University of California, Santa Barbara .-Biography:...
k-norm of M.
The first of the Ky Fan norms, the Ky Fan 1-norm is the same as the operator norm
Operator norm
In mathematics, the operator norm is a means to measure the "size" of certain linear operators. Formally, it is a norm defined on the space of bounded linear operators between two given normed vector spaces.- Introduction and definition :...
of M as a linear operator with respect to the Euclidean norms of Km and Kn. In other words, the Ky Fan 1-norm is the operator norm induced by the standard l2 Euclidean inner product. For this reason, it is also called the operator 2-norm. One can easily verify the relationship between the Ky Fan 1-norm and singular values. It is true in general, for a bounded operator M on (possibly infinite dimensional) Hilbert spaces
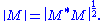
But, in the matrix case, M*M½ is a normal matrix
Normal matrix
A complex square matrix A is a normal matrix ifA^*A=AA^* \ where A* is the conjugate transpose of A. That is, a matrix is normal if it commutes with its conjugate transpose.If A is a real matrix, then A*=AT...
, so ||M* M||½ is the largest eigenvalue of M* M½, i.e. the largest singular value of M.
The last of the Ky Fan norms, the sum of all singular values, is the trace norm
Trace class
In mathematics, a trace class operator is a compact operator for which a trace may be defined, such that the trace is finite and independent of the choice of basis....
(also known as the 'nuclear norm'), defined by ||M|| = Tr[(M*M)½] (the diagonal entries of M* M are the squares of the singular values).
Hilbert–Schmidt norm
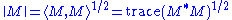The singular values are related to another norm on the space of operators. Consider the Hilbert–Schmidt inner product on the n × n matrices, defined by. So the induced norm is . Since trace is invariant under unitary equivalence, this shows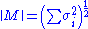where
are the singular values of M. This is called the Frobenius norm, Schatten 2-norm, or Hilbert–Schmidt norm of M. Direct calculation shows that if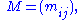the Frobenius norm of M coincides with
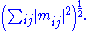
Tensor SVD
Unfortunately, the problem of finding a low rank approximation to a tensor is ill-posed. In other words, there doesn't exist a best possible solution, but instead a sequence of better and better approximations that converge to infinitely large matrices. But in spite of this, there are several ways of attempting this decomposition.There exist two types of tensor decompositions which generalise SVD to multi-way arrays. One decomposition decomposes a tensor into a sum of rank-1 tensors, see Candecomp-PARAFAC (CP) algorithm. The CP algorithm should not be confused with a rank-R decomposition but, for a given N, it decomposes a tensor into a sum of N rank-1 tensors that optimally fit the original tensor. The second type of decomposition computes the orthonormal subspaces associated with the different axes or modes of a tensor (orthonormal row space, column space, fiber space, etc.). This decomposition is referred to in the literature as the Tucker3/TuckerM
Tucker decomposition
In mathematics, Tucker decomposition decomposes a tensor into a set of matrices and one small core tensor. It is named after Ledyard R. Tuckeralthough it goes back to Hitchcock in 1927....
, M-mode SVD, multilinear SVD and sometimes referred to as a higher-order SVD (HOSVD). In addition, multilinear principal component analysis
Multilinear principal component analysis
Multilinear principal-component analysis is a mathematical procedure that uses multiple orthogonal transformations to convert a set of multidimensional objects into another set of multidimensional objects of lower dimensions. There is one orthogonal transformation for each dimension...
in multilinear subspace learning
Multilinear subspace learning
Multilinear subspace learning aims to learn a specific small part of a large space of multidimensional objects having a particular desired property. It is a dimensionality reduction approach for finding a low-dimensional representation with certain preferred characteristics of high-dimensional...
involves the same mathematical operations as Tucker decomposition, being used in a different context of dimensionality reduction
Dimensionality reduction
In machine learning, dimension reduction is the process of reducing the number of random variables under consideration, and can be divided into feature selection and feature extraction.-Feature selection:...
.
Bounded operators on Hilbert spaces
The factorization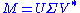 can be extended to a bounded operatorBounded operator
In functional analysis, a branch of mathematics, a bounded linear operator is a linear transformation L between normed vector spaces X and Y for which the ratio of the norm of L to that of v is bounded by the same number, over all non-zero vectors v in X...
M on a separable Hilbert space H. Namely, for any bounded operator M, there exist a partial isometry
Partial isometry
In functional analysis a partial isometry is a linear map W between Hilbert spaces H and K such that the restriction of W to the orthogonal complement of its kernel is an isometry...
U, a unitary V, a measure space (X, μ), and a non-negative measurable f such that
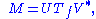
where
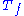is the multiplication by fMultiplication operator
In operator theory, a multiplication operator is a linear operator T defined on some vector space of functions and whose value at a function φ is given by multiplication by a fixed function f...
on L2(X, μ).
This can be shown by mimicking the linear algebraic argument for the matricial case above. VTf V* is the unique positive square root of M*M, as given by the Borel functional calculus
Borel functional calculus
In functional analysis, a branch of mathematics, the Borel functional calculus is a functional calculus , which has particularly broad scope. Thus for instance if T is an operator, applying the squaring function s → s2 to T yields the operator T2...
for self adjoint operators. The reason why U need not be unitary is because, unlike the finite dimensional case, given an isometry U1 with non trivial kernel, a suitable U2 may not be found such that
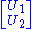
is a unitary operator.
As for matrices, the singular value factorization is equivalent to the polar decomposition for operators: we can simply write
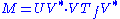
and notice that U V* is still a partial isometry while VTf V* is positive.
Singular values and compact operators
To extend notion of singular values and left/right-singular vectors to the operator case, one needs to restrict to compact operatorsCompact operator on Hilbert space
In functional analysis, compact operators on Hilbert spaces are a direct extension of matrices: in the Hilbert spaces, they are precisely the closure of finite-rank operators in the uniform operator topology. As such, results from matrix theory can sometimes be extended to compact operators using...
. It is a general fact that compact operators on Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s have only discrete spectrum. This is also true for compact operators on Hilbert spaces, since Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
s are a special case of Banach spaces. If T is compact, every nonzero λ in its spectrum is an eigenvalue. Furthermore, a compact self adjoint operator can be diagonalized by its eigenvectors. If M is compact, so is M*M. Applying the diagonalization result, the unitary image of its positive square root Tf has a set of orthonormal eigenvectors {ei} corresponding to strictly positive eigenvalues {σi}. For any ψ ∈ H,
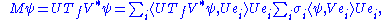
where the series converges in the norm topology on H. Notice how this resembles the expression from the finite dimensional case. The σi 's are called the singular values of M. {U ei} and {V ei} can be considered the left- and right-singular vectors of M respectively.
Compact operators on a Hilbert space
Compact operator on Hilbert space
In functional analysis, compact operators on Hilbert spaces are a direct extension of matrices: in the Hilbert spaces, they are precisely the closure of finite-rank operators in the uniform operator topology. As such, results from matrix theory can sometimes be extended to compact operators using...
are the closure of finite-rank operators in the uniform operator topology. The above series expression gives an explicit such representation. An immediate consequence of this is:
Theorem M is compact if and only if M*M is compact.
History
The singular value decomposition was originally developed by differential geometers, who wished to determine whether a real bilinear form could be made equal to another by independent orthogonal transformations of the two spaces it acts on. Eugenio BeltramiEugenio Beltrami
Eugenio Beltrami was an Italian mathematician notable for his work concerning differential geometry and mathematical physics...
and Camille Jordan
Camille Jordan
Marie Ennemond Camille Jordan was a French mathematician, known both for his foundational work in group theory and for his influential Cours d'analyse. He was born in Lyon and educated at the École polytechnique...
discovered independently, in 1873 and 1874 respectively, that the singular values of the bilinear forms, represented as a matrix, form a complete set
Complete set of invariants
In mathematics, a complete set of invariants for a classification problem is a collection of mapsf_i : X \to Y_i \,, such that x ∼ x' if and only if f_i = f_i for all i...
of invariant
Invariant (mathematics)
In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
s for bilinear forms under orthogonal substitutions. James Joseph Sylvester
James Joseph Sylvester
James Joseph Sylvester was an English mathematician. He made fundamental contributions to matrix theory, invariant theory, number theory, partition theory and combinatorics...
also arrived at the singular value decomposition for real square matrices in 1889, apparently independent of both Beltrami and Jordan. Sylvester called the singular values the canonical multipliers of the matrix A. The fourth mathematician to discover the singular value decomposition independently is Autonne in 1915, who arrived at it via the polar decomposition. The first proof of the singular value decomposition for rectangular and complex matrices seems to be by Carl Eckart
Carl Eckart
Carl Henry Eckart was an American physicist, physical oceanographer, geophysicist, and administrator. He co-developed the Wigner-Eckart theorem and is also known for the Eckart conditions in quantum mechanics.-Education:Eckart began college in 1919 at Washington University in St...
and Gale Young in 1936; they saw it as a generalization of the principal axis transformation for Hermitian matrices.
In 1907, Erhard Schmidt
Erhard Schmidt
Erhard Schmidt was a German mathematician whose work significantly influenced the direction of mathematics in the twentieth century. He was born in Tartu, Governorate of Livonia . His advisor was David Hilbert and he was awarded his doctorate from Georg-August University of Göttingen in 1905...
defined an analog of singular values for integral operators (which are compact, under some weak technical assumptions); it seems he was unaware of the parallel work on singular values of finite matrices. This theory was further developed by Émile Picard in 1910, who is the first to call the numbers
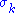singular values (or rather, valeurs singulières).Practical methods for computing the SVD date back to Kogbetliantz
Ervand Kogbetliantz
Ervand George Kogbetliantz Dr. Kogbetliantz was an Armenian/American mathematician and the first president of the Yerevan State University. He left Russia in 1918. He received a Doctorate in mathematics from the University of Paris in 1923...
in 1954, 1955 and Hestenes
Magnus Hestenes
Magnus Rudolph Hestenes was an American mathematician. Together with Cornelius Lanczos and Eduard Stiefel, he invented the conjugate gradient method....
in 1958. resembling closely the Jacobi eigenvalue algorithm
Jacobi eigenvalue algorithm
In numerical linear algebra, the Jacobi eigenvalue algorithm is an iterative method for the calculation of the eigenvalues and eigenvectors of a real symmetric matrix...
, which uses plane rotations or Givens rotations. However, these were replaced by the method of Gene Golub
Gene H. Golub
Gene Howard Golub , Fletcher Jones Professor of Computer Science at Stanford University, was one of the preeminent numerical analysts of his generation....
and William Kahan
William Kahan
William Morton Kahan is a mathematician and computer scientist who received the Turing Award in 1989 for "his fundamental contributions to numerical analysis", and was named an ACM Fellow in 1994....
published in 1965, which uses Householder transformation
Householder transformation
In linear algebra, a Householder transformation is a linear transformation that describes a reflection about a plane or hyperplane containing the origin. Householder transformations are widely used in numerical linear algebra, to perform QR decompositions and in the first step of the QR algorithm...
s or reflections.
In 1970, Golub and Christian Reinsch published a variant of the Golub/Kahan algorithm that is still the one most-used today.
See also
- Canonical correlation analysis (CCA)
- Canonical formCanonical formGenerally, in mathematics, a canonical form of an object is a standard way of presenting that object....
- Correspondence analysisCorrespondence analysisCorrespondence analysis is a multivariate statistical technique proposed by Hirschfeld and later developed by Jean-Paul Benzécri. It is conceptually similar to principal component analysis, but applies to categorical rather than continuous data...
(CA) - Curse of dimensionalityCurse of dimensionalityThe curse of dimensionality refers to various phenomena that arise when analyzing and organizing high-dimensional spaces that do not occur in low-dimensional settings such as the physical space commonly modeled with just three dimensions.There are multiple phenomena referred to by this name in...
- Digital signal processingDigital signal processingDigital signal processing is concerned with the representation of discrete time signals by a sequence of numbers or symbols and the processing of these signals. Digital signal processing and analog signal processing are subfields of signal processing...
- Dimension reduction
- Eigendecomposition
- Empirical orthogonal functionsEmpirical orthogonal functionsIn statistics and signal processing, the method of empirical orthogonal function analysis is a decomposition of a signal or data set in terms of orthogonal basis functions which are determined from the data. It is the same as performing a principal components analysis on the data, except that the...
(EOFs) - Fourier analysis
- Fourier-related transforms
- Generalized singular value decompositionGeneralized singular value decompositionIn linear algebra the generalized singular value decomposition is a matrix decomposition more general than the singular value decomposition...
- Latent semantic analysisLatent semantic analysisLatent semantic analysis is a technique in natural language processing, in particular in vectorial semantics, of analyzing relationships between a set of documents and the terms they contain by producing a set of concepts related to the documents and terms. LSA assumes that words that are close...
- Latent semantic indexingLatent semantic indexingLatent Semantic Indexing is an indexing and retrieval method that uses a mathematical technique called Singular value decomposition to identify patterns in the relationships between the terms and concepts contained in an unstructured collection of text. LSI is based on the principle that words...
- Linear least squaresLinear least squaresIn statistics and mathematics, linear least squares is an approach to fitting a mathematical or statistical model to data in cases where the idealized value provided by the model for any data point is expressed linearly in terms of the unknown parameters of the model...
- Locality sensitive hashingLocality sensitive hashingLocality-sensitive hashing is a method of performing probabilistic dimension reduction of high-dimensional data. The basic idea is to hash the input items so that similar items are mapped to the same buckets with high probability .-Definition:An LSH family \mathcal F is defined fora...
- Matrix decompositionMatrix decompositionIn the mathematical discipline of linear algebra, a matrix decomposition is a factorization of a matrix into some canonical form. There are many different matrix decompositions; each finds use among a particular class of problems.- Example :...
- Multilinear principal component analysisMultilinear principal component analysisMultilinear principal-component analysis is a mathematical procedure that uses multiple orthogonal transformations to convert a set of multidimensional objects into another set of multidimensional objects of lower dimensions. There is one orthogonal transformation for each dimension...
(MPCA) - Nearest neighbor searchNearest neighbor searchNearest neighbor search , also known as proximity search, similarity search or closest point search, is an optimization problem for finding closest points in metric spaces. The problem is: given a set S of points in a metric space M and a query point q ∈ M, find the closest point in S to q...
- Non-linear iterative partial least squaresNon-linear iterative partial least squaresIn statistics, non-linear iterative partial least squares is an algorithm for computing the first few components in a principal component or partial least squares analysis. For very high-dimensional datasets, such as those generated in the 'omics sciences it is usually only necessary to compute...
- Polar decomposition
- Principal components analysisPrincipal components analysisPrincipal component analysis is a mathematical procedure that uses an orthogonal transformation to convert a set of observations of possibly correlated variables into a set of values of uncorrelated variables called principal components. The number of principal components is less than or equal to...
(PCA) - Singular value
- Time seriesTime seriesIn statistics, signal processing, econometrics and mathematical finance, a time series is a sequence of data points, measured typically at successive times spaced at uniform time intervals. Examples of time series are the daily closing value of the Dow Jones index or the annual flow volume of the...
- von Neumann's trace inequality
- Wavelet compression
Libraries that support complex and real SVD
- LAPACKLAPACK-External links:* : a modern replacement for PLAPACK and ScaLAPACK* on Netlib.org* * * : a modern replacement for LAPACK that is MultiGPU ready* on Sourceforge.net* * optimized LAPACK for Solaris OS on SPARC/x86/x64 and Linux* * *...
(website), the Linear Algebra Package. The user manual gives details of subroutines to calculate the SVD (see also http://www.netlib.org/lapack/lug/node32.html). - LINPACK Z (website), Linear Algebra Library. Has officially been superseded by LAPACK, but it includes a C version of SVD for complex numbers.
- For the PythonPython (programming language)Python is a general-purpose, high-level programming language whose design philosophy emphasizes code readability. Python claims to "[combine] remarkable power with very clear syntax", and its standard library is large and comprehensive...
programming language:- NumPy (NumPy is module for numerical computing with arrays and matrices)
- SciPy (SciPySciPySciPy is an open source library of algorithms and mathematical tools for the Python programming language.SciPy contains modules for optimization, linear algebra, integration, interpolation, special functions, FFT, signal and image processing, ODE solvers and other tasks common in science and...
contains many numerical routines)
Libraries that support real SVD
- GNU Scientific LibraryGNU Scientific LibraryIn computing, the GNU Scientific Library is a software library written in the C programming language for numerical calculations in applied mathematics and science...
(website), a numerical C/C++ library supporting SVD (see http://www.gnu.org/software/gsl/manual/html_node/Singular-Value-Decomposition.html). - For the PythonPython (programming language)Python is a general-purpose, high-level programming language whose design philosophy emphasizes code readability. Python claims to "[combine] remarkable power with very clear syntax", and its standard library is large and comprehensive...
programming language:- NumPy (NumPy is module for numerical computing with arrays and matrices)
- SciPy (SciPySciPySciPy is an open source library of algorithms and mathematical tools for the Python programming language.SciPy contains modules for optimization, linear algebra, integration, interpolation, special functions, FFT, signal and image processing, ODE solvers and other tasks common in science and...
contains many numerical routines) - Gensim, efficient randomized algorithm on top of NumPy; unlike other implementations, allows SVD of matrices larger than RAM (incremental online SVD).
- sparsesvd, Python wrapper of SVDLIBC.
- SVD-Python, pure Python SVD under GNU GPL.
- ALGLIB, includes a partial port of the LAPACK to C++, C#, Delphi, Visual Basic, etc.
- JAMA, a Java matrix package provided by the NIST.
- COLT, a Java package for High Performance Scientific and Technical Computing, provided by CERNCERNThe European Organization for Nuclear Research , known as CERN , is an international organization whose purpose is to operate the world's largest particle physics laboratory, which is situated in the northwest suburbs of Geneva on the Franco–Swiss border...
. - Eigen, a templated C++ implementation.
- redsvd, efficient randomized algorithm on top of C++ Eigen.
- PROPACK, computes the SVD of large and sparse or structured matrices, in Fortran 77.
- SVDPACK, a library in ANSI FORTRAN 77 implementing four iterative SVD methods. Includes C and C++ interfaces.
- SVDLIBC, re-writing of SVDPACK in C, with minor bug fixes.
- SVDLIBJ, a Java port of SVDLIBC. (Also available as an executable .jar similar to SVDLIBC in the S-Space Package)
- SVDLIBC# SVDLIBC converted to C#.
- dANN part of the linear algebra package of the dANNDannDann may refer to:* Dann, the surname* dANN, the artificial intelligence software libraryDann as a surname may refer to:* Mary Dann and Carrie Dann, Native American activists* Colin Dann, a British author* Jack Dann, a American writer...
java Artificial IntelligenceArtificial intelligenceArtificial intelligence is the intelligence of machines and the branch of computer science that aims to create it. AI textbooks define the field as "the study and design of intelligent agents" where an intelligent agent is a system that perceives its environment and takes actions that maximize its...
library by Syncleus, Inc. - GraphLab GraphLab collaborative filtering library, large scale parallel implementation of SVD (in C++) for multicore.
Texts and demonstrations
- MIT Lecture series by Gilbert StrangGilbert StrangWilliam Gilbert Strang , usually known as simply Gilbert Strang or Gil Strang, is a renowned American mathematician, with contributions to finite element theory, the calculus of variations, wavelet analysis and linear algebra...
. See Lecture #29 on the SVD (scroll down to the bottom till you see "Singular Value Decomposition"). The first 17 minutes give the overview. Then Prof. Strang works two examples. Then the last 4 minutes (min 36 to min 40) are a summary. You can probably fast forward the examples, but the first and last are an excellent concise visual presentation of the topic. - Applications of SVD on PC Hansen's web site.
- Introduction to the Singular Value Decomposition by Todd Will of the University of Wisconsin—La Crosse. This site has animations for the visual minded as well as demonstrations of compression using SVD.
- Los Alamos group's book chapter has helpful gene data analysis examples.
- SVD, another explanation of singular value decomposition
- SVD Tutorial, yet another explanation of SVD. Very intuitive.
- Javascript script demonstrating SVD more extensively, paste your data from a spreadsheet.
- http://www.stasegem.be/shop2/SVD.htm demonstrating SVD recommender system (same as above but how to make your own recommender matrix
- Chapter from "Numerical Recipes in C" gives more information about implementation and applications of SVD. (Acrobat DRM plug-in required)
- Online Matrix Calculator Performs singular value decomposition of matrices.
- A simple tutorial on SVD and applications of Spectral Methods
- Matrix and Tensor Decompositions in Genomic Signal Processing
- SVD on MathWorld, with image compression as an example application.
- Notes on Rank-K Approximation (and SVD for the uninitiated) at The University of Texas at Austin. This demo with Octave uses the data file lenna.m.
- If you liked this... New York Times article on SVD in movie-ratings and NetflixNetflixNetflix, Inc., is an American provider of on-demand internet streaming media in the United States, Canada, and Latin America and flat rate DVD-by-mail in the United States. The company was established in 1997 and is headquartered in Los Gatos, California...
- David Austin, We Recommend a Singular Value Decomposition, Featured Column from the AMS, August 2009.
Songs
- It Had To Be U is a song, written by Michael Greenacre, about the singular value decomposition, explaining its definition and role in statistical dimension reduction. It was first performed at the joint meetings of the 9th Tartu Conference on Multivariate Statistics and 20th International Workshop on Matrices and Statistics, in Tartu, Estonia, June 2011.