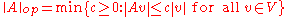Operator norm
Encyclopedia
In mathematics
, the operator norm is a means to measure the "size" of certain linear operators. Formally, it is a norm
defined on the space of bounded linear operators between two given normed vector space
s.
, either the real number
s R or the complex number
s C), a linear map A : V → W is continuous if and only if there exists a real number c such that
(the norm on the left is the one in W, the norm on the right is the one in V). Intuitively, the continuous operator A never "lengthens" any vector more than by a factor of c. Thus the image of a bounded set under a continuous operator is also bounded. Because of this property, the continuous linear operators are also known as bounded operator
s. In order to "measure the size" of A, it then seems natural to take the smallest number c such that the above inequality holds for all v in V. In other words, we measure the "size" of A by how much it "lengthens" vectors in the "biggest" case. So we define the operator norm of A as
(the minimum exists as the set of all such c is closed
, nonempty
, and bounded
from below).
yields a linear map from Rn to Rm. One can put several different norms on these spaces, as explained in the article on norms
. Each such choice of norms gives rise to an operator norm and therefore yields a norm on the space of all m-by-n matrices. Examples can be found in the article on matrix norms.
If we specifically choose the Euclidean norm on both Rn and Rm, then we obtain the matrix norm which to a given matrix A assigns the square root
of the largest eigenvalue of the matrix A*A (where A* denotes the conjugate transpose
of A). This is equivalent to assigning the largest singular value of A.
Passing to a typical infinite dimensional example, consider the sequence space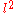
defined by
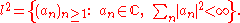
This can be viewed as an infinite dimensional analogue of the Euclidean space Cn. Now take a bounded sequence
s = (sn ). The sequence s is an element of the space l ∞, with a norm given by
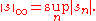
Define an operator Ts by simply multiplication:
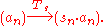
The operator T s is bounded with operator norm

One can extend this discussion directly to the case where l 2 is replaced by a general Lp space with p > 1 and l∞ replaced by L∞.
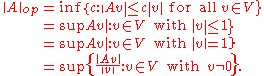
s between V and W. This means


The following inequality is an immediate consequence of the definition:
The operator norm is also compatible with the composition, or multiplication, of operators: if V, W and X are three normed spaces over the same base field, and A : V → W and B: W → X are two bounded operators, then
For bounded operators on V, this implies that operator multiplication is jointly continuous.
It follows from the definition that a sequence of operators converge in operator norm means they converge uniformly on bounded sets.
. If A : H → H is a bounded linear operator, then we have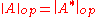
and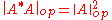
where A* denotes the adjoint operator of A (which in Euclidean Hilbert spaces with the standard inner product corresponds to the conjugate transpose
of the matrix A).
In general, the spectral radius
of A is bounded above by the operator norm of A:
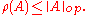
To see why equality may not always hold, consider the Jordan canonical form of a matrix in the finite dimensional case. Because there are non-zero entries on the superdiagonal, equality may be violated. The quasinilpotent operators is one class of such examples. A nonzero quasinilpotent operator A has spectrum {0}. So ρ(A) = 0 while ||A||op > 0.
However, when a matrix N is normal
, its Jordan canonical form is diagonal (up to unitary equivalence); this is the spectral theorem
. In that case it is easy to see that

The spectral theorem can be extended to normal operator
s in general. Therefore the above equality holds for any bounded normal operator N. This formula can sometimes be used to compute the operator norm of a given bounded operator A: define the Hermitian operator H = A*A, determine its spectral radius, and take the square root
to obtain the operator norm of A.
The space of bounded operators on H, with the topology induced by operator norm, is not separable. For example, consider the Hilbert space L2[0,1
]. For 0 < t ≤ 1, let Ωt be the characteristic function
of [0,t], and Pt be the multiplication operator
given by Ωt , i.e.

Then each Pt is a bounded operator with operator norm 1 and
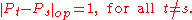
But {Pt} is an uncountable set. This implies the space of bounded operators on L2[0,1] is not separable, in operator norm. One can compare this with the fact that the sequence space l ∞ is not separable.
The set of all bounded operators on a Hilbert space, together with the operator norm and the adjoint operation, yields a C*-algebra.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the operator norm is a means to measure the "size" of certain linear operators. Formally, it is a norm
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
defined on the space of bounded linear operators between two given normed vector space
Normed vector space
In mathematics, with 2- or 3-dimensional vectors with real-valued entries, the idea of the "length" of a vector is intuitive and can easily be extended to any real vector space Rn. The following properties of "vector length" are crucial....
s.
Introduction and definition
Given two normed vector spaces V and W (over the same base fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
, either the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s R or the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s C), a linear map A : V → W is continuous if and only if there exists a real number c such that
(the norm on the left is the one in W, the norm on the right is the one in V). Intuitively, the continuous operator A never "lengthens" any vector more than by a factor of c. Thus the image of a bounded set under a continuous operator is also bounded. Because of this property, the continuous linear operators are also known as bounded operator
Bounded operator
In functional analysis, a branch of mathematics, a bounded linear operator is a linear transformation L between normed vector spaces X and Y for which the ratio of the norm of L to that of v is bounded by the same number, over all non-zero vectors v in X...
s. In order to "measure the size" of A, it then seems natural to take the smallest number c such that the above inequality holds for all v in V. In other words, we measure the "size" of A by how much it "lengthens" vectors in the "biggest" case. So we define the operator norm of A as
(the minimum exists as the set of all such c is closed
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
, nonempty
Empty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
, and bounded
Bounded set
In mathematical analysis and related areas of mathematics, a set is called bounded, if it is, in a certain sense, of finite size. Conversely, a set which is not bounded is called unbounded...
from below).
Examples
Every real m-by-n matrixMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
yields a linear map from Rn to Rm. One can put several different norms on these spaces, as explained in the article on norms
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
. Each such choice of norms gives rise to an operator norm and therefore yields a norm on the space of all m-by-n matrices. Examples can be found in the article on matrix norms.
If we specifically choose the Euclidean norm on both Rn and Rm, then we obtain the matrix norm which to a given matrix A assigns the square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
of the largest eigenvalue of the matrix A*A (where A* denotes the conjugate transpose
Conjugate transpose
In mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...
of A). This is equivalent to assigning the largest singular value of A.
Passing to a typical infinite dimensional example, consider the sequence space
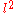
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
defined by
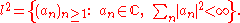
This can be viewed as an infinite dimensional analogue of the Euclidean space Cn. Now take a bounded sequence
s = (sn ). The sequence s is an element of the space l ∞, with a norm given by
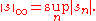
Define an operator Ts by simply multiplication:
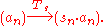
The operator T s is bounded with operator norm

One can extend this discussion directly to the case where l 2 is replaced by a general Lp space with p > 1 and l∞ replaced by L∞.
Equivalent definitions
One can show that the following definitions are all equivalent: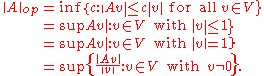
Properties
The operator norm is indeed a norm on the space of all bounded operatorBounded operator
In functional analysis, a branch of mathematics, a bounded linear operator is a linear transformation L between normed vector spaces X and Y for which the ratio of the norm of L to that of v is bounded by the same number, over all non-zero vectors v in X...
s between V and W. This means



The following inequality is an immediate consequence of the definition:

The operator norm is also compatible with the composition, or multiplication, of operators: if V, W and X are three normed spaces over the same base field, and A : V → W and B: W → X are two bounded operators, then

For bounded operators on V, this implies that operator multiplication is jointly continuous.
It follows from the definition that a sequence of operators converge in operator norm means they converge uniformly on bounded sets.
Operators on a Hilbert space
Suppose H is a real or complex Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
. If A : H → H is a bounded linear operator, then we have
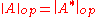
and
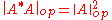
where A* denotes the adjoint operator of A (which in Euclidean Hilbert spaces with the standard inner product corresponds to the conjugate transpose
Conjugate transpose
In mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...
of the matrix A).
In general, the spectral radius
Spectral radius
In mathematics, the spectral radius of a square matrix or a bounded linear operator is the supremum among the absolute values of the elements in its spectrum, which is sometimes denoted by ρ.-Matrices:...
of A is bounded above by the operator norm of A:
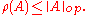
To see why equality may not always hold, consider the Jordan canonical form of a matrix in the finite dimensional case. Because there are non-zero entries on the superdiagonal, equality may be violated. The quasinilpotent operators is one class of such examples. A nonzero quasinilpotent operator A has spectrum {0}. So ρ(A) = 0 while ||A||op > 0.
However, when a matrix N is normal
Normal matrix
A complex square matrix A is a normal matrix ifA^*A=AA^* \ where A* is the conjugate transpose of A. That is, a matrix is normal if it commutes with its conjugate transpose.If A is a real matrix, then A*=AT...
, its Jordan canonical form is diagonal (up to unitary equivalence); this is the spectral theorem
Spectral theorem
In mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized...
. In that case it is easy to see that

The spectral theorem can be extended to normal operator
Normal operator
In mathematics, especially functional analysis, a normal operator on a complex Hilbert space H is a continuous linear operatorN:H\to Hthat commutes with its hermitian adjoint N*: N\,N^*=N^*N....
s in general. Therefore the above equality holds for any bounded normal operator N. This formula can sometimes be used to compute the operator norm of a given bounded operator A: define the Hermitian operator H = A*A, determine its spectral radius, and take the square root
Square root of a matrix
In mathematics, the square root of a matrix extends the notion of square root from numbers to matrices. A matrix B is said to be a square root of A if the matrix product B · B is equal to A.-Properties:...
to obtain the operator norm of A.
The space of bounded operators on H, with the topology induced by operator norm, is not separable. For example, consider the Hilbert space L2[0,1
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
]. For 0 < t ≤ 1, let Ωt be the characteristic function
Characteristic function
In mathematics, characteristic function can refer to any of several distinct concepts:* The most common and universal usage is as a synonym for indicator function, that is the function* In probability theory, the characteristic function of any probability distribution on the real line is given by...
of [0,t], and Pt be the multiplication operator
Multiplication operator
In operator theory, a multiplication operator is a linear operator T defined on some vector space of functions and whose value at a function φ is given by multiplication by a fixed function f...
given by Ωt , i.e.

Then each Pt is a bounded operator with operator norm 1 and
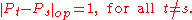
But {Pt} is an uncountable set. This implies the space of bounded operators on L2[0,1] is not separable, in operator norm. One can compare this with the fact that the sequence space l ∞ is not separable.
The set of all bounded operators on a Hilbert space, together with the operator norm and the adjoint operation, yields a C*-algebra.