Quantum information
Encyclopedia
In quantum mechanics
, quantum information is physical information
that is held in the "state" of a quantum system. The most popular unit of quantum information is the qubit
, a two-level quantum system. However, unlike classical digital states (which are discrete), a two-state quantum system can actually be in a superposition
of the two states at any given time.
Quantum information differs from classical information in several respects, among which we note the following:
However, despite this, the amount of information that can be retrieved in a single qubit is equal to one bit. It is in the processing of information (quantum computation) that the differentiation occurs.
The ability to manipulate quantum information enables us to perform tasks that would be unachievable in a classical context, such as unconditionally secure transmission of information. Quantum information processing is the most general field that is concerned with quantum information. There are certain tasks which classical computer
s cannot perform "efficiently" (that is, in polynomial time) according to any known algorithm. However, a quantum computer can compute the answer to some of these problems in polynomial time; one well-known example of this is Shor's factoring algorithm
. Other algorithms can speed up a task less dramatically—for example, Grover's search algorithm
which gives a quadratic speed-up over the best possible classical algorithm.
Quantum information, and changes in quantum information, can be quantitatively measured by using an analogue of Shannon entropy
, called the von Neumann
entropy
. Given a statistical ensemble of quantum mechanical systems with the density matrix
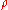, it is given by
Many of the same entropy measures in classical information theory can also be generalized to the quantum case, such as Holevo entropy and the conditional quantum entropy
.
to the quantum world. Quantum information theory aims to answer the following question:
One of the strengths of classical information theory is that physical representation of information can be disregarded: There is no need for an 'ink-on-paper' information theory or a 'DVD information' theory. This is because it is always possible to efficiently transform information from one representation to another. However, this is not the case for quantum information: it is not possible, for example, to write down on paper the previously unknown information contained in the polarisation of a photon.
In general, quantum mechanics does not allow us to read out the state of a quantum system with arbitrary precision. The existence of Bell correlations
between quantum systems cannot be converted into classical information. It is only possible to transform quantum information between quantum systems of sufficient information capacity. The information content of a message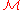
can, for this reason, be measured in terms of the minimum number n of two-level systems which are needed to store the message: 
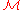consists of n qubit
s. In its original theoretical sense, the term qubit is thus a measure for the amount of information. A two-level quantum system can carry at most one qubit, in the same sense a classical binary digit can carry at most one classical bit.
As a consequence of the noisy-channel coding theorem, noise limits the information content of an analog information carrier to be finite. It is very difficult to protect the remaining finite information content of analog information carriers against noise. The example of classical analog information shows that quantum information processing schemes must necessarily be tolerant against noise, otherwise there would not be a chance for them to be useful. It was a big breakthrough for the theory of quantum information, when quantum error correction codes and fault-tolerant quantum computation schemes were discovered.
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, quantum information is physical information
Physical information
In physics, physical information refers generally to the information that is contained in a physical system. Its usage in quantum mechanics In physics, physical information refers generally to the information that is contained in a physical system. Its usage in quantum mechanics In physics,...
that is held in the "state" of a quantum system. The most popular unit of quantum information is the qubit
Qubit
In quantum computing, a qubit or quantum bit is a unit of quantum information—the quantum analogue of the classical bit—with additional dimensions associated to the quantum properties of a physical atom....
, a two-level quantum system. However, unlike classical digital states (which are discrete), a two-state quantum system can actually be in a superposition
Quantum superposition
Quantum superposition is a fundamental principle of quantum mechanics. It holds that a physical system exists in all its particular, theoretically possible states simultaneously; but, when measured, it gives a result corresponding to only one of the possible configurations.Mathematically, it...
of the two states at any given time.
Quantum information differs from classical information in several respects, among which we note the following:
- It cannot be read without the state becoming the measured value,
- An arbitrary state cannot be clonedNo cloning theoremThe no-cloning theorem is a result of quantum mechanics that forbids the creation of identical copies of an arbitrary unknown quantum state. It was stated by Wootters, Zurek, and Dieks in 1982, and has profound implications in quantum computing and related fields.The state of one system can be...
, - The state may be in a superposition of basis values.
However, despite this, the amount of information that can be retrieved in a single qubit is equal to one bit. It is in the processing of information (quantum computation) that the differentiation occurs.
The ability to manipulate quantum information enables us to perform tasks that would be unachievable in a classical context, such as unconditionally secure transmission of information. Quantum information processing is the most general field that is concerned with quantum information. There are certain tasks which classical computer
Computer
A computer is a programmable machine designed to sequentially and automatically carry out a sequence of arithmetic or logical operations. The particular sequence of operations can be changed readily, allowing the computer to solve more than one kind of problem...
s cannot perform "efficiently" (that is, in polynomial time) according to any known algorithm. However, a quantum computer can compute the answer to some of these problems in polynomial time; one well-known example of this is Shor's factoring algorithm
Shor's algorithm
Shor's algorithm, named after mathematician Peter Shor, is a quantum algorithm for integer factorization formulated in 1994...
. Other algorithms can speed up a task less dramatically—for example, Grover's search algorithm
Grover's algorithm
Grover's algorithm is a quantum algorithm for searching an unsorted database with N entries in O time and using O storage space . It was invented by Lov Grover in 1996....
which gives a quadratic speed-up over the best possible classical algorithm.
Quantum information, and changes in quantum information, can be quantitatively measured by using an analogue of Shannon entropy
Information entropy
In information theory, entropy is a measure of the uncertainty associated with a random variable. In this context, the term usually refers to the Shannon entropy, which quantifies the expected value of the information contained in a message, usually in units such as bits...
, called the von Neumann
John von Neumann
John von Neumann was a Hungarian-American mathematician and polymath who made major contributions to a vast number of fields, including set theory, functional analysis, quantum mechanics, ergodic theory, geometry, fluid dynamics, economics and game theory, computer science, numerical analysis,...
entropy
Von Neumann entropy
In quantum statistical mechanics, von Neumann entropy, named after John von Neumann, is the extension of classical entropy concepts to the field of quantum mechanics....
. Given a statistical ensemble of quantum mechanical systems with the density matrix
Density matrix
In quantum mechanics, a density matrix is a self-adjoint positive-semidefinite matrix of trace one, that describes the statistical state of a quantum system...
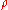, it is given byMany of the same entropy measures in classical information theory can also be generalized to the quantum case, such as Holevo entropy and the conditional quantum entropy
Conditional quantum entropy
The conditional quantum entropy is an entropy measure used in quantum information theory. It is a generalization of the conditional entropy of classical information theory...
.
Quantum information theory
The theory of quantum information is a result of the effort to generalise classical information theoryInformation theory
Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
to the quantum world. Quantum information theory aims to answer the following question:
What happens if information is stored in a state of a quantum system?
One of the strengths of classical information theory is that physical representation of information can be disregarded: There is no need for an 'ink-on-paper' information theory or a 'DVD information' theory. This is because it is always possible to efficiently transform information from one representation to another. However, this is not the case for quantum information: it is not possible, for example, to write down on paper the previously unknown information contained in the polarisation of a photon.
In general, quantum mechanics does not allow us to read out the state of a quantum system with arbitrary precision. The existence of Bell correlations
Bell state
The Bell states are a concept in quantum information science and represent the simplest possible examples of entanglement. They are named after John S. Bell, as they are the subject of his famous Bell inequality. An EPR pair is a pair of qubits which jointly are in a Bell state, that is, entangled...
between quantum systems cannot be converted into classical information. It is only possible to transform quantum information between quantum systems of sufficient information capacity. The information content of a message
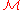can, for this reason, be measured in terms of the minimum number n of two-level systems which are needed to store the message: 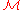consists of n qubitQubit
In quantum computing, a qubit or quantum bit is a unit of quantum information—the quantum analogue of the classical bit—with additional dimensions associated to the quantum properties of a physical atom....
s. In its original theoretical sense, the term qubit is thus a measure for the amount of information. A two-level quantum system can carry at most one qubit, in the same sense a classical binary digit can carry at most one classical bit.
As a consequence of the noisy-channel coding theorem, noise limits the information content of an analog information carrier to be finite. It is very difficult to protect the remaining finite information content of analog information carriers against noise. The example of classical analog information shows that quantum information processing schemes must necessarily be tolerant against noise, otherwise there would not be a chance for them to be useful. It was a big breakthrough for the theory of quantum information, when quantum error correction codes and fault-tolerant quantum computation schemes were discovered.
See also
- Quantum clockQuantum ClockA quantum clock is a type of clock that confines aluminum and beryllium ions together in an electromagnetic trap and cools them by lasers to near absolute zero temperatures. Developed by National Institute of Standards and Technology physicists, the clock is 37 times more precise than the existing...
- Quantum computing
- Quantum statistical mechanicsQuantum statistical mechanicsQuantum statistical mechanics is the study of statistical ensembles of quantum mechanical systems. A statistical ensemble is described by a density operator S, which is a non-negative, self-adjoint, trace-class operator of trace 1 on the Hilbert space H describing the quantum system. This can be...
- POVMPOVMIn functional analysis and quantum measurement theory, a POVM is a measure whose values are non-negative self-adjoint operators on a Hilbert space. It is the most general formulation of a measurement in the theory of quantum physics...
(positive operator valued measure) - Information theoryInformation theoryInformation theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
- Quantum gravityQuantum gravityQuantum gravity is the field of theoretical physics which attempts to develop scientific models that unify quantum mechanics with general relativity...
Journals
Among the journals in this field are- International Journal of Quantum InformationInternational Journal of Quantum InformationThe International Journal of Quantum Information was established in 2003 and is published by World Scientific. It covers the field of quantum information science, with topics on areas such as quantum metrology, quantum cryptography, quantum computation, and quantum mechanics.- Abstracting and...
- Journal of Quantum Chemistry
- Applied Mathematics & Information Sciences
External links and references
- Lectures at the Institut Henri Poincaré (slides and videos)
- Quantum Information Theory at ETH Zurich
- Quantum Information Perimeter Institute for Theoretical Physics
- Center for Quantum Computation - The CQC, part of Cambridge University, is a group of researchers studying quantum information, and is a useful portal for those interested in this field.
- Quantum Information Group The quantum information research group at the University of NottinghamUniversity of NottinghamThe University of Nottingham is a public research university based in Nottingham, United Kingdom, with further campuses in Ningbo, China and Kuala Lumpur, Malaysia...
. - Qwiki - A quantum physics wiki devoted to providing technical resources for practicing quantum information scientists.
- Quantiki - A wiki portal for quantum information with introductory tutorials.
- Charles H. Bennett and Peter W. Shor, "Quantum Information Theory," IEEE Transactions on Information Theory, Vol 44, pp 2724–2742, Oct 1998
- Institute for Quantum Computing - The Institute for Quantum Computing, based in Waterloo, ON Canada, is a research institute working in conjunction with the University of Waterloo and Perimeter Institute on the subject of Quantum Information.
- Quantum information can be negative
- Gregg Jaeger's book on Quantum Information(published by Springer, New York, 2007, ISBN 0-387-35725-4)
- The International Conference on Quantum Information (ICQI)
- New Trends in Quantum Computation, Stony Brook, 2010
- Institute of Quantum Information Caltech
- Quantum Information Theory Imperial College
- Quantum Information Technology Toshiba Research
- International Journal of Quantum Information World Scientific
- Quantum Information Processing Springer
- USC Center for Quantum Information Science & Technology
- Center for Quantum Information and Control Theoretical and experimental groups from University of New Mexico and University of Arizona.
- Mark M. Wilde, "From Classical to Quantum Shannon Theory", arXiv:1106.1445.