Kabsch algorithm
Encyclopedia
The Kabsch algorithm, named after Wolfgang Kabsch, is a method for calculating the optimal rotation matrix that minimizes the RMSD (root mean square
d deviation) between two paired sets of points. It is useful in graphics, cheminformatics
to compare molecular structures, and also bioinformatics
for comparing protein
structures (in particular, see root-mean-square deviation (bioinformatics)).
The algorithm only computes the rotation matrix, but it also requires the computation of a translation vector. When both the translation and rotation are actually performed, the algorithm is sometimes called partial Procrustes superimposition (see also orthogonal Procrustes problem
).
. The first row is the coordinates of the first point, the second row is the coordinates of the second point, the Nth row is the coordinates of the Nth point.
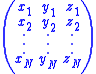
The algorithm works in three steps: a translation, the computation of a covariance matrix, and the computation of the optimal rotation matrix.
coincides with the origin of the coordinate system
. This is done by subtracting from the point coordinates the coordinates of the respective centroid.
A. In matrix notation,
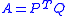
or, using summation notation,
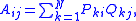
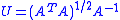but implementing a numerical solution to this formula becomes complicated when all special cases are accounted for (for example, the case of A not having an inverse).
If singular value decomposition
(SVD) routines are available, the optimal rotation, U, can be calculated using the following simple algorithm.
First, calculate the SVD of the covariance matrix A.
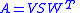
Next, decide whether we need to correct our rotation matrix to insure a right-handed coordinate system
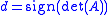
Finally, calculate our optimal rotation matrix, U, as
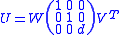
Coutsias, Seok, and Dill have found an equivalent method that uses quaternion
s.
A Matlab
function is available at http://www.mathworks.com/matlabcentral/fileexchange/25746-kabsch-algorithm
A free PyMol
plugin easily implementing Kabsch is Cealign. VMD
uses the Kabsch algorithm for its alignment.
Root mean square
In mathematics, the root mean square , also known as the quadratic mean, is a statistical measure of the magnitude of a varying quantity. It is especially useful when variates are positive and negative, e.g., sinusoids...
d deviation) between two paired sets of points. It is useful in graphics, cheminformatics
Cheminformatics
Cheminformatics is the use of computer and informational techniques, applied to a range of problems in the field of chemistry. These in silico techniques are used in pharmaceutical companies in the process of drug discovery...
to compare molecular structures, and also bioinformatics
Bioinformatics
Bioinformatics is the application of computer science and information technology to the field of biology and medicine. Bioinformatics deals with algorithms, databases and information systems, web technologies, artificial intelligence and soft computing, information and computation theory, software...
for comparing protein
Protein
Proteins are biochemical compounds consisting of one or more polypeptides typically folded into a globular or fibrous form, facilitating a biological function. A polypeptide is a single linear polymer chain of amino acids bonded together by peptide bonds between the carboxyl and amino groups of...
structures (in particular, see root-mean-square deviation (bioinformatics)).
The algorithm only computes the rotation matrix, but it also requires the computation of a translation vector. When both the translation and rotation are actually performed, the algorithm is sometimes called partial Procrustes superimposition (see also orthogonal Procrustes problem
Orthogonal Procrustes problem
The orthogonal Procrustes problem is a matrix approximation problem in linear algebra. In its classical form, one is given two matrices A and B and asked to find an orthogonal matrix R which most closely maps A to B...
).
Description
The algorithm starts with two sets of paired points, P and Q. Each set of points can be represented as an N×3 matrixMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
. The first row is the coordinates of the first point, the second row is the coordinates of the second point, the Nth row is the coordinates of the Nth point.
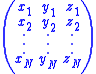
The algorithm works in three steps: a translation, the computation of a covariance matrix, and the computation of the optimal rotation matrix.
Translation
Both sets of coordinates must be translated first, so that their centroidCentroid
In geometry, the centroid, geometric center, or barycenter of a plane figure or two-dimensional shape X is the intersection of all straight lines that divide X into two parts of equal moment about the line. Informally, it is the "average" of all points of X...
coincides with the origin of the coordinate system
Coordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
. This is done by subtracting from the point coordinates the coordinates of the respective centroid.
Computation of the covariance matrix
The second step consist of calculating a covariance matrixCovariance matrix
In probability theory and statistics, a covariance matrix is a matrix whose element in the i, j position is the covariance between the i th and j th elements of a random vector...
A. In matrix notation,
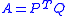
or, using summation notation,
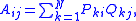
Computation of the optimal rotation matrix
It is possible to calculate the optimal rotation U based on the matrix formula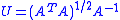 but implementing a numerical solution to this formula becomes complicated when all special cases are accounted for (for example, the case of A not having an inverse).If singular value decomposition
Singular value decomposition
In linear algebra, the singular value decomposition is a factorization of a real or complex matrix, with many useful applications in signal processing and statistics....
(SVD) routines are available, the optimal rotation, U, can be calculated using the following simple algorithm.
First, calculate the SVD of the covariance matrix A.
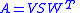
Next, decide whether we need to correct our rotation matrix to insure a right-handed coordinate system
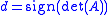
Finally, calculate our optimal rotation matrix, U, as
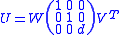
Coutsias, Seok, and Dill have found an equivalent method that uses quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s.
Generalizations
The algorithm was described for points in a three-dimensional space. The generalization to D dimensions is immediate.External links
This SVD algorithm is described in more detail at http://cnx.org/content/m11608/latest/A Matlab
MATLAB
MATLAB is a numerical computing environment and fourth-generation programming language. Developed by MathWorks, MATLAB allows matrix manipulations, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other languages,...
function is available at http://www.mathworks.com/matlabcentral/fileexchange/25746-kabsch-algorithm
A free PyMol
PyMOL
PyMOL is an open-source, user-sponsored, molecular visualization system created by Warren Lyford DeLano and commercialized by DeLano Scientific LLC, which is a private software company dedicated to creating useful tools that become universally accessible to scientific and educational communities...
plugin easily implementing Kabsch is Cealign. VMD
Visual Molecular Dynamics
- External links :* * *...
uses the Kabsch algorithm for its alignment.