
Null space
Encyclopedia
In linear algebra
, the kernel or null space (also nullspace) of a matrix
A is the set of all vectors x for which Ax = 0. The kernel of a matrix with n columns is a linear subspace
of n-dimensional Euclidean space
. The dimension
of the null space of A is called the nullity of A.
If viewed as a linear transformation
, the null space of a matrix is precisely the kernel of the mapping (i.e. the set of vectors that map to zero). For this reason, the kernel of a linear transformation between abstract vector space
s is sometimes referred to as the null space of the transformation.
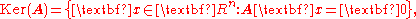
where 0 denotes the zero vector with m components. The matrix equation Ax = 0 is equivalent to a homogeneous system of linear equations: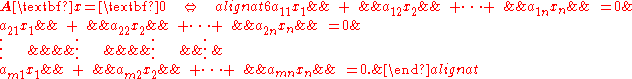
From this viewpoint, the null space of A is the same as the solution set to the homogeneous system.
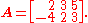
The null space of this matrix consists of all vectors (x, y, z) ∈ R3 for which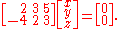
This can be written as a homogeneous system of linear equations involving x, y, and z: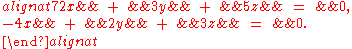
This can be written in matrix form as: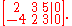
Using Gauss-Jordan reduction, this reduces to: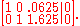
Rewriting yields: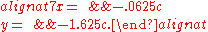
Now we can write the null space (solution to Ax = 0) in terms of c (which is our free variable), where c is scalar
: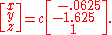
The null space of A is precisely the set of solutions to these equations (in this case, a line
through the origin in R3).
of Rn. That is, the set Null(A) has the following three properties:
Here are the proofs:
. This makes it possible to use row reduction to find a basis
for the null space:
For example, suppose that the reduced row echelon form of A is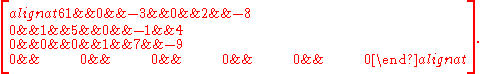
Then the solutions to the homogeneous system given in parametric form with x3, x5, and x6 as free variables are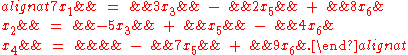
Which can be rewritten as
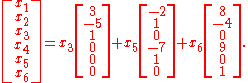
Therefore, the three vectors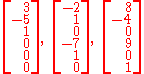
are a basis for the null space of A.
of vectors as follows:
Here a1, ..., am denote the rows of the matrix A. It follows that x is in the null space of A if and only if x is orthogonal
(or perpendicular) to each of the row vectors of A (because if the dot product of two vectors is equal to zero they are by definition orthogonal).
The row space
of a matrix A is the span
of the row vectors of A. By the above reasoning, the null space of A is the orthogonal complement to the row space. That is, a vector x lies in the null space of A if and only if it is perpendicular to every vector in the row space of A.
The dimension of the row space of A is called the rank
of A, and the dimension of the null space of A is called the nullity of A. These quantities are related by the equation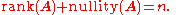
The equation above is known as the rank-nullity theorem
.
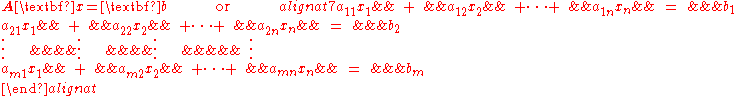
If u and v are two possible solutions to the above equation, then
Thus, the difference of any two solutions to the equation Ax = b lies in the null space of A.
It follows that any solution to the equation Ax = b can be expressed as the sum of a fixed solution v and an arbitrary element of the null space. That is, the solution set to the equation Ax = b is
where v is any fixed vector satisfying Av = b. Geometrically, this says that the solution set to Ax = b is the translation
of the null space of A by the vector v. See also Fredholm alternative
.
of a column vector. The left null space of A is the same as the null space of AT. The left null space of A is the orthogonal complement to the column space
of A, and is the cokernel
of the associated linear transformation. The null space, the row space, the column space, and the left null space of A are the four fundamental subspaces associated to the matrix A.
s, the null space (or kernel
) of a linear transformation
T: V → W is the set of all vectors in V that map to zero: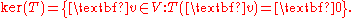
If we represent the linear transformation by a matrix, then the kernel of the transformation is precisely the null space of the matrix.
, presented in introductory linear algebra textbooks and in the preceding sections of this article are not suitable for a practical computation of the null space because of numerical accuracy problems in the presence of rounding errors. Namely, the computation may greatly amplify the rounding errors, which are inevitable in all but textbook examples on integers, and so give completely wrong results. For this reason, methods based on introductory linear algebra texts are generally not suitable for implementation in software; rather, one should consult contemporary numerical analysis
sources for an algorithm like the one below, which does not amplify rounding errors unnecessarily.
A state-of-the-art approach is based on singular value decomposition (SVD)
. This approach can be also easily programmed using standard libraries, such as LAPACK
. SVD of matrix A computes unitary matrices U and V and a rectangular diagonal matrix S of the same size as A with nonnegative diagonal entries, such that
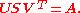
Denote the columns of V by

the diagonal entries of S by
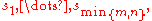
and put
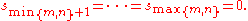
(The numbers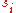 are called the singular values of A.)
are called the singular values of A.)
Then the columns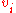 of V such that the corresponding
of V such that the corresponding  form an orthonormal basis of the nullspace of A.
form an orthonormal basis of the nullspace of A.
This can be seen as follows: First note that if we have one solution y of the equation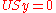 , then also
, then also  for unit vectors
for unit vectors 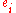 with
with  . Now if we solve
. Now if we solve 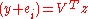 for z, then
for z, then 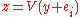 because of
because of 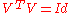 , which means that the i'th column of V spans one direction of the null space.
, which means that the i'th column of V spans one direction of the null space.
In a numerical computation, the singular values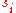 are taken to be zero when they are less than some small tolerance. For example, the tolerance can be taken to be
are taken to be zero when they are less than some small tolerance. For example, the tolerance can be taken to be
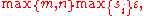
where is the machine epsilon
is the machine epsilon
of the computer, that is, the smallest number such that in the floating point
arithmetics of the computer,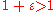 . For the IEEE 64 bit floating point format,
. For the IEEE 64 bit floating point format, 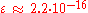 .
.
Computation of the SVD of a matrix generally costs about the same as several matrix-matrix multiplications with matrices of the same size when state-of-the art implementation (accurate up to rounding precision) is used, such as in LAPACK. This is true even if, in theory, the SVD cannot be computed by a finite number of operations, so an iterative method with stopping tolerances based on rounding precision must be employed. The cost of the SVD approach is several times higher than computing the null space by reduction, but it should be acceptable whenever reliability is important. It is also possible to compute the null space by the QR decomposition
, with the numerical stability and the cost both being between those of the SVD and the reduction approaches.
The computation of a null space basis using the QR decomposition is explained in more detail below.
Let A be a mxn matrix with m < n. Using the QR factorization of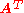 , we can find a matrix
, we can find a matrix
such that ,
,
where P is a permutation matrix, Q is nxn and R is nxm. Matrix
is nxm and consists of the first m columns of Q. Matrix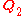 is nx(n-m) and is
is nx(n-m) and is
made up of Q 's last n-m columns. Since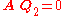 , the columns of
, the columns of
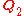 span the null space of A.
span the null space of A.
, Introduction to the Null Space of a Matrix
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, the kernel or null space (also nullspace) of a matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
A is the set of all vectors x for which Ax = 0. The kernel of a matrix with n columns is a linear subspace
Euclidean subspace
In linear algebra, a Euclidean subspace is a set of vectors that is closed under addition and scalar multiplication. Geometrically, a subspace is a flat in n-dimensional Euclidean space that passes through the origin...
of n-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
. The dimension
Dimension (vector space)
In mathematics, the dimension of a vector space V is the cardinality of a basis of V. It is sometimes called Hamel dimension or algebraic dimension to distinguish it from other types of dimension...
of the null space of A is called the nullity of A.
If viewed as a linear transformation
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
, the null space of a matrix is precisely the kernel of the mapping (i.e. the set of vectors that map to zero). For this reason, the kernel of a linear transformation between abstract vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s is sometimes referred to as the null space of the transformation.
Definition
The kernel of an m × n matrix A is the set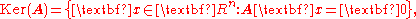
where 0 denotes the zero vector with m components. The matrix equation Ax = 0 is equivalent to a homogeneous system of linear equations:
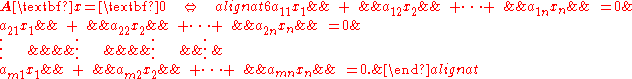
From this viewpoint, the null space of A is the same as the solution set to the homogeneous system.
Example
Consider the matrix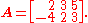
The null space of this matrix consists of all vectors (x, y, z) ∈ R3 for which
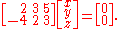
This can be written as a homogeneous system of linear equations involving x, y, and z:
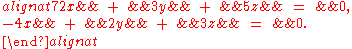
This can be written in matrix form as:
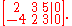
Using Gauss-Jordan reduction, this reduces to:
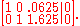
Rewriting yields:
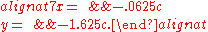
Now we can write the null space (solution to Ax = 0) in terms of c (which is our free variable), where c is scalar
Scalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
:
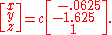
The null space of A is precisely the set of solutions to these equations (in this case, a line
Line (mathematics)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
through the origin in R3).
Subspace properties
The null space of an m × n matrix is a subspaceEuclidean subspace
In linear algebra, a Euclidean subspace is a set of vectors that is closed under addition and scalar multiplication. Geometrically, a subspace is a flat in n-dimensional Euclidean space that passes through the origin...
of Rn. That is, the set Null(A) has the following three properties:
- Null(A) always contains the zero vector.
- If x ∈ Null(A) and y ∈ Null(A), then x + y ∈ Null(A).
- If x ∈ Null(A) and c is a scalarScalar (mathematics)In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
, then c x ∈ Null(A).
Here are the proofs:
- A0 = 0.
- If Ax = 0 and Ay = 0, then A(x + y) = Ax + Ay = 0 + 0 = 0.
- If Ax = 0 and c is a scalar, then A(cx) = cAx = c0 = 0.
Basis
The null space of a matrix is not affected by elementary row operationsElementary row operations
In mathematics, an elementary matrix is a simple matrix which differs from the identity matrix by one single elementary row operation. The elementary matrices generate the general linear group of invertible matrices...
. This makes it possible to use row reduction to find a basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
for the null space:
- Input An m × n matrix A.
- Output A basis for the null space of A
- Use elementary row operations to put A in reduced row echelon formRow echelon formIn linear algebra a matrix is in row echelon form if* All nonzero rows are above any rows of all zeroes, and...
. - Interpreting the reduced row echelon form as a homogeneous linear system, determine which of the variables x1, x2, ..., xn are free. Write equations for the dependent variables in terms of the free variables.
- For each free variable xi, choose the vector in the null space for which xi = 1 and the remaining free variables are zero. The resulting collection of vectors is a basis for the null space of A.
- Use elementary row operations to put A in reduced row echelon form
For example, suppose that the reduced row echelon form of A is
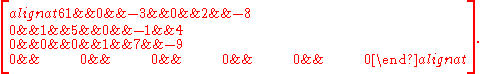
Then the solutions to the homogeneous system given in parametric form with x3, x5, and x6 as free variables are
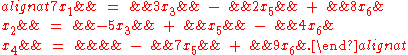
Which can be rewritten as
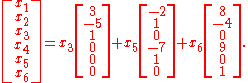
Therefore, the three vectors

are a basis for the null space of A.
Relation to the row space
Let A be an m by n matrix (i.e., A has m rows and n columns). The product of A and the n-dimensional vector x can be written in terms of the dot productDot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
of vectors as follows:

Here a1, ..., am denote the rows of the matrix A. It follows that x is in the null space of A if and only if x is orthogonal
Orthogonality
Orthogonality occurs when two things can vary independently, they are uncorrelated, or they are perpendicular.-Mathematics:In mathematics, two vectors are orthogonal if they are perpendicular, i.e., they form a right angle...
(or perpendicular) to each of the row vectors of A (because if the dot product of two vectors is equal to zero they are by definition orthogonal).
The row space
Row space
In linear algebra, the row space of a matrix is the set of all possible linear combinations of its row vectors. The row space of an m × n matrix is a subspace of n-dimensional Euclidean space...
of a matrix A is the span
Linear span
In the mathematical subfield of linear algebra, the linear span of a set of vectors in a vector space is the intersection of all subspaces containing that set...
of the row vectors of A. By the above reasoning, the null space of A is the orthogonal complement to the row space. That is, a vector x lies in the null space of A if and only if it is perpendicular to every vector in the row space of A.
The dimension of the row space of A is called the rank
Rank (linear algebra)
The column rank of a matrix A is the maximum number of linearly independent column vectors of A. The row rank of a matrix A is the maximum number of linearly independent row vectors of A...
of A, and the dimension of the null space of A is called the nullity of A. These quantities are related by the equation
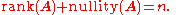
The equation above is known as the rank-nullity theorem
Rank-nullity theorem
In mathematics, the rank–nullity theorem of linear algebra, in its simplest form, states that the rank and the nullity of a matrix add up to the number of columns of the matrix. Specifically, if A is an m-by-n matrix over some field, thenThis applies to linear maps as well...
.
Nonhomogeneous equations
The null space also plays a role in the solution to a nonhomogeneous system of linear equations: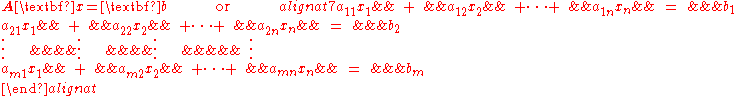
If u and v are two possible solutions to the above equation, then

Thus, the difference of any two solutions to the equation Ax = b lies in the null space of A.
It follows that any solution to the equation Ax = b can be expressed as the sum of a fixed solution v and an arbitrary element of the null space. That is, the solution set to the equation Ax = b is

where v is any fixed vector satisfying Av = b. Geometrically, this says that the solution set to Ax = b is the translation
Translation (geometry)
In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...
of the null space of A by the vector v. See also Fredholm alternative
Fredholm alternative
In mathematics, the Fredholm alternative, named after Ivar Fredholm, is one of Fredholm's theorems and is a result in Fredholm theory. It may be expressed in several ways, as a theorem of linear algebra, a theorem of integral equations, or as a theorem on Fredholm operators...
.
Left null space
The left null space of a matrix A consists of all vectors x such that xTA = 0T, where T denotes the transposeTranspose
In linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:...
of a column vector. The left null space of A is the same as the null space of AT. The left null space of A is the orthogonal complement to the column space
Column space
In linear algebra, the column space of a matrix is the set of all possible linear combinations of its column vectors. The column space of an m × n matrix is a subspace of m-dimensional Euclidean space...
of A, and is the cokernel
Cokernel
In mathematics, the cokernel of a linear mapping of vector spaces f : X → Y is the quotient space Y/im of the codomain of f by the image of f....
of the associated linear transformation. The null space, the row space, the column space, and the left null space of A are the four fundamental subspaces associated to the matrix A.
Null space of a transformation
If V and W are vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s, the null space (or kernel
Kernel (mathematics)
In mathematics, the word kernel has several meanings. Kernel may mean a subset associated with a mapping:* The kernel of a mapping is the set of elements that map to the zero element , as in kernel of a linear operator and kernel of a matrix...
) of a linear transformation
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
T: V → W is the set of all vectors in V that map to zero:
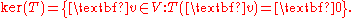
If we represent the linear transformation by a matrix, then the kernel of the transformation is precisely the null space of the matrix.
Numerical computation of null space
Algorithms based on row or column reduction, that is, Gaussian eliminationGaussian elimination
In linear algebra, Gaussian elimination is an algorithm for solving systems of linear equations. It can also be used to find the rank of a matrix, to calculate the determinant of a matrix, and to calculate the inverse of an invertible square matrix...
, presented in introductory linear algebra textbooks and in the preceding sections of this article are not suitable for a practical computation of the null space because of numerical accuracy problems in the presence of rounding errors. Namely, the computation may greatly amplify the rounding errors, which are inevitable in all but textbook examples on integers, and so give completely wrong results. For this reason, methods based on introductory linear algebra texts are generally not suitable for implementation in software; rather, one should consult contemporary numerical analysis
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
sources for an algorithm like the one below, which does not amplify rounding errors unnecessarily.
A state-of-the-art approach is based on singular value decomposition (SVD)
Singular value decomposition
In linear algebra, the singular value decomposition is a factorization of a real or complex matrix, with many useful applications in signal processing and statistics....
. This approach can be also easily programmed using standard libraries, such as LAPACK
LAPACK
-External links:* : a modern replacement for PLAPACK and ScaLAPACK* on Netlib.org* * * : a modern replacement for LAPACK that is MultiGPU ready* on Sourceforge.net* * optimized LAPACK for Solaris OS on SPARC/x86/x64 and Linux* * *...
. SVD of matrix A computes unitary matrices U and V and a rectangular diagonal matrix S of the same size as A with nonnegative diagonal entries, such that
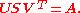
Denote the columns of V by

the diagonal entries of S by
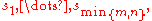
and put
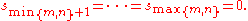
(The numbers
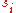 are called the singular values of A.)
are called the singular values of A.)Then the columns
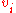 of V such that the corresponding
of V such that the corresponding  form an orthonormal basis of the nullspace of A.
form an orthonormal basis of the nullspace of A.This can be seen as follows: First note that if we have one solution y of the equation
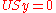 , then also
, then also  for unit vectors
for unit vectors 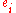 with
with  . Now if we solve
. Now if we solve 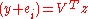 for z, then
for z, then 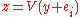 because of
because of 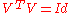 , which means that the i'th column of V spans one direction of the null space.
, which means that the i'th column of V spans one direction of the null space.In a numerical computation, the singular values
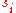 are taken to be zero when they are less than some small tolerance. For example, the tolerance can be taken to be
are taken to be zero when they are less than some small tolerance. For example, the tolerance can be taken to be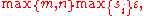
where
 is the machine epsilon
is the machine epsilonMachine epsilon
Machine epsilon gives an upper bound on the relative error due to rounding in floating point arithmetic. This value characterizes computer arithmetic in the field of numerical analysis, and by extension in the subject of computational science...
of the computer, that is, the smallest number such that in the floating point
Floating point
In computing, floating point describes a method of representing real numbers in a way that can support a wide range of values. Numbers are, in general, represented approximately to a fixed number of significant digits and scaled using an exponent. The base for the scaling is normally 2, 10 or 16...
arithmetics of the computer,
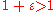 . For the IEEE 64 bit floating point format,
. For the IEEE 64 bit floating point format, 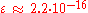 .
.Computation of the SVD of a matrix generally costs about the same as several matrix-matrix multiplications with matrices of the same size when state-of-the art implementation (accurate up to rounding precision) is used, such as in LAPACK. This is true even if, in theory, the SVD cannot be computed by a finite number of operations, so an iterative method with stopping tolerances based on rounding precision must be employed. The cost of the SVD approach is several times higher than computing the null space by reduction, but it should be acceptable whenever reliability is important. It is also possible to compute the null space by the QR decomposition
QR decomposition
In linear algebra, a QR decomposition of a matrix is a decomposition of a matrix A into a product A=QR of an orthogonal matrix Q and an upper triangular matrix R...
, with the numerical stability and the cost both being between those of the SVD and the reduction approaches.
The computation of a null space basis using the QR decomposition is explained in more detail below.
Let A be a mxn matrix with m < n. Using the QR factorization of
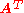 , we can find a matrix
, we can find a matrixsuch that
 ,
,where P is a permutation matrix, Q is nxn and R is nxm. Matrix

is nxm and consists of the first m columns of Q. Matrix
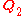 is nx(n-m) and is
is nx(n-m) and ismade up of Q 's last n-m columns. Since
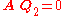 , the columns of
, the columns of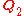 span the null space of A.
span the null space of A.See also
- Matrix (mathematics)Matrix (mathematics)In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
- Kernel (algebra)Kernel (algebra)In the various branches of mathematics that fall under the heading of abstract algebra, the kernel of a homomorphism measures the degree to which the homomorphism fails to be injective. An important special case is the kernel of a matrix, also called the null space.The definition of kernel takes...
- Euclidean subspaceEuclidean subspaceIn linear algebra, a Euclidean subspace is a set of vectors that is closed under addition and scalar multiplication. Geometrically, a subspace is a flat in n-dimensional Euclidean space that passes through the origin...
- System of linear equations
- Row spaceRow spaceIn linear algebra, the row space of a matrix is the set of all possible linear combinations of its row vectors. The row space of an m × n matrix is a subspace of n-dimensional Euclidean space...
- Column spaceColumn spaceIn linear algebra, the column space of a matrix is the set of all possible linear combinations of its column vectors. The column space of an m × n matrix is a subspace of m-dimensional Euclidean space...
or Image (matrix)Column spaceIn linear algebra, the column space of a matrix is the set of all possible linear combinations of its column vectors. The column space of an m × n matrix is a subspace of m-dimensional Euclidean space... - Row reduction
- Four fundamental subspaces
Numerical analysis textbooks
- Lloyd N. Trefethen and David Bau, III, Numerical Linear Algebra, SIAM 1997, ISBN 978-0898713619 online version
External links
, MIT Linear Algebra Lecture on the Four Fundamental Subspaces at Google Video, from MIT OpenCourseWareMIT OpenCourseWare
MIT OpenCourseWare is an initiative of the Massachusetts Institute of Technology to put all of the educational materials from its undergraduate- and graduate-level courses online, partly free and openly available to anyone, anywhere. MIT OpenCourseWare is a large-scale, web-based publication of...
, Introduction to the Null Space of a Matrix

