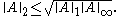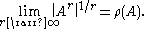Matrix norm
Encyclopedia
In mathematics
, a matrix norm is a natural extension of the notion of a vector norm to matrices
.
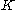 will denote the field
will denote the field
of real
or complex number
s. Let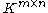 denote the vector space
denote the vector space
containing all matrices with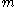 rows and
rows and  columns with entries in
columns with entries in 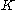 . Throughout the article
. Throughout the article 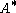 denotes the conjugate transpose
denotes the conjugate transpose
of matrix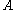 .
.
A matrix norm is a vector norm on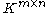 . That is, if
. That is, if 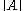 denotes the norm of the matrix
denotes the norm of the matrix 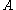 , then,
, then,
Additionally, in the case of square matrices (thus, m = n), some (but not all) matrix norms satisfy the following condition, which is related to the fact that matrices are more than just vectors:
A matrix norm that satisfies this additional property is called a sub-multiplicative norm ( in some books, the terminology matrix norm is used only for those norms which are sub-multiplicative). The set of all n-by-n matrices, together with such a sub-multiplicative norm, is an example of a Banach algebra
.
or complex number
s), then one defines the corresponding induced norm or operator norm
on the space of m-by-n matrices as the following maxima: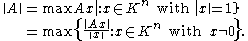
These are different from the entrywise p-norms and the Schatten p-norms for matrices treated below, which are also usually denoted
by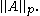
If m = n and one uses the same norm on the domain and the range, then the induced operator norm is a sub-multiplicative matrix norm.
The operator norm corresponding to the p-norm for vectors is:
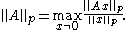
In the case of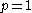 and
and 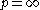 , the norms can be computed as:
, the norms can be computed as:
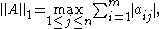 which is simply the maximum absolute column sum of the matrix.
which is simply the maximum absolute column sum of the matrix.
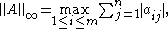 which is simply the maximum absolute row sum of the matrix
which is simply the maximum absolute row sum of the matrix
For example, if the matrix A is defined by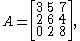
then we have ||A||1 = max(5,13,19) = 19. and ||A||∞ = max(15,12,10) = 15. Consider another example
where we add all the entries in each column and determine the greatest value, which results in ||A||1 = max (6,13,11,8) = 13.
We can do the same for the rows and get ||A||∞ = max(9,11,9,9) = 11. Thus 11 is our max.
In the special case of p = 2 (the Euclidean norm) and m = n (square matrices), the induced matrix norm is the spectral norm. The spectral norm of a matrix A is the largest singular value of A i.e. the square root of the largest eigenvalue of the positive-semidefinite matrix A*A: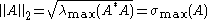
where A* denotes the conjugate transpose
of A.
More generally, one can define the subordinate matrix norm on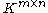 induced by
induced by
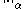 on
on 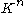 , and
, and 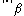 on
on 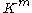 as:
as: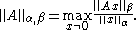
Subordinate norms are consistent with the norms that induce them, giving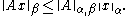
Any induced norm satisfies the inequality
where ρ(A) is the spectral radius
of A. For a symmetric or hermitian matrix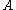 , we have equality for the 2-norm, since in this case the 2-norm is the spectral radius of
, we have equality for the 2-norm, since in this case the 2-norm is the spectral radius of 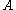 . For an arbitrary matrix, we may not have equality for any . Take
. For an arbitrary matrix, we may not have equality for any . Take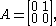
the spectral radius of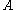 is 0, but
is 0, but 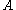 is not the zero matrix, and so none of the induced norms are equal to the spectral radius of
is not the zero matrix, and so none of the induced norms are equal to the spectral radius of 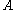 .
.
Furthermore,
for square matrices
we have the spectral radius formula:
 matrix as a vector of size
matrix as a vector of size 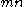 , and
, and
use one of the familiar vector norms.
For example, using the p-norm for vectors, we get:
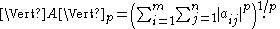
This is a different norm from the induced p-norm (see above) and the Schatten p-norm (see below), but the notation is the same.
The special case p = 2 is the Frobenius norm, and p = ∞ yields the maximum norm.
. This norm can be defined in various ways:
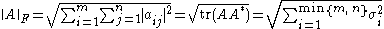
where A* denotes the conjugate transpose
of A, σi are the singular values of A, and the trace function is used. The Frobenius norm is very similar to the Euclidean norm on Kn and comes from an inner product on the space of all matrices.
The Frobenius norm is sub-multiplicative and is very useful for numerical linear algebra
. This norm is often easier to compute than induced norms.
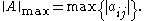
This norm is not sub-multiplicative.
of a matrix. If the singular values are denoted by σi, then the Schatten p-norm is defined by
These norms again share the notation with the induced and entrywise p-norms, but they are different.
All Schatten norms are sub-multiplicative. They are also unitarily invariant, which means that ||A|| = ||UAV|| for all matrices A and all unitary matrices U and V.
The most familiar cases are p = 1, 2, ∞. The case p = 2 yields the Frobenius norm, introduced before. The case p = ∞ yields the spectral norm, which is the matrix norm induced by the vector 2-norm (see above). Finally, p = 1 yields the nuclear norm (also known as the trace norm, or the Ky Fan 'n'-norm), defined as
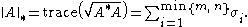
(Here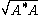 denotes a matrix
denotes a matrix  such that
such that 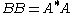 . More precisely, since
. More precisely, since 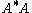 is a positive semidefinite matrix, its square root
is a positive semidefinite matrix, its square root
is well-defined.)
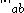 on
on  is called consistent with a vector norm
is called consistent with a vector norm 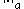 on
on 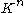 and a vector norm
and a vector norm 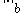 on
on 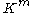 if:
if: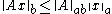
for all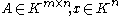 . All induced norms are consistent by definition.
. All induced norms are consistent by definition.
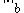 on
on 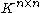 is called compatible with a vector norm
is called compatible with a vector norm 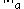 on
on 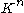 if:
if: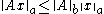
for all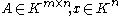 . Induced norms are compatible by definition.
. Induced norms are compatible by definition.

for some positive numbers r and s, for all matrices A in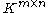 . In other words, they are equivalent norms; they induce the same topology
. In other words, they are equivalent norms; they induce the same topology
on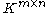 . This is a special case of the equivalence of norms in finite-dimensional Normed vector spaces.
. This is a special case of the equivalence of norms in finite-dimensional Normed vector spaces.
Moreover, for every vector norm on
on 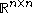 , there exists a unique positive real number
, there exists a unique positive real number 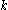 such that
such that 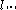 is a sub-multiplicative matrix norm for every
is a sub-multiplicative matrix norm for every 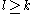 .
.
A matrix norm ||·||α is said to be minimal if there exists no other matrix norm ||·||β satisfying ||·||β ≤ ||·||α.
 the following inequalities hold:
the following inequalities hold:
Here, ||·||p refers to the matrix norm induced by the vector p-norm.
Another useful inequality between matrix norms is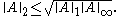
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a matrix norm is a natural extension of the notion of a vector norm to matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
.
Definition
In what follows,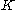 will denote the field
will denote the fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
of real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
or complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s. Let
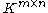 denote the vector space
denote the vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
containing all matrices with
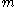 rows and
rows and  columns with entries in
columns with entries in 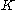 . Throughout the article
. Throughout the article 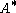 denotes the conjugate transpose
denotes the conjugate transposeConjugate transpose
In mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...
of matrix
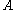 .
.A matrix norm is a vector norm on
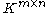 . That is, if
. That is, if 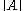 denotes the norm of the matrix
denotes the norm of the matrix 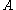 , then,
, then,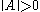 if
if  and
and 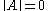 iffIFFIFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...
iffIFFIFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...

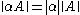 for all
for all  in
in 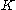 and all matrices
and all matrices  in
in 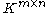
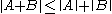 for all matrices
for all matrices 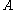 and
and 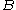 in
in 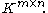
Additionally, in the case of square matrices (thus, m = n), some (but not all) matrix norms satisfy the following condition, which is related to the fact that matrices are more than just vectors:
 for all matrices
for all matrices 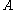 and
and 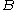 in
in 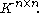
A matrix norm that satisfies this additional property is called a sub-multiplicative norm ( in some books, the terminology matrix norm is used only for those norms which are sub-multiplicative). The set of all n-by-n matrices, together with such a sub-multiplicative norm, is an example of a Banach algebra
Banach algebra
In mathematics, especially functional analysis, a Banach algebra, named after Stefan Banach, is an associative algebra A over the real or complex numbers which at the same time is also a Banach space...
.
Induced norm
If vector norms on Km and Kn are given (K is field of realReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
or complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s), then one defines the corresponding induced norm or operator norm
Operator norm
In mathematics, the operator norm is a means to measure the "size" of certain linear operators. Formally, it is a norm defined on the space of bounded linear operators between two given normed vector spaces.- Introduction and definition :...
on the space of m-by-n matrices as the following maxima:
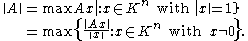
These are different from the entrywise p-norms and the Schatten p-norms for matrices treated below, which are also usually denoted
by
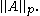
If m = n and one uses the same norm on the domain and the range, then the induced operator norm is a sub-multiplicative matrix norm.
The operator norm corresponding to the p-norm for vectors is:
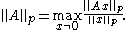
In the case of
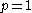 and
and 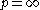 , the norms can be computed as:
, the norms can be computed as: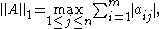 which is simply the maximum absolute column sum of the matrix.
which is simply the maximum absolute column sum of the matrix.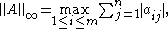 which is simply the maximum absolute row sum of the matrix
which is simply the maximum absolute row sum of the matrixFor example, if the matrix A is defined by
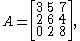
then we have ||A||1 = max(5,13,19) = 19. and ||A||∞ = max(15,12,10) = 15. Consider another example

where we add all the entries in each column and determine the greatest value, which results in ||A||1 = max (6,13,11,8) = 13.
We can do the same for the rows and get ||A||∞ = max(9,11,9,9) = 11. Thus 11 is our max.
In the special case of p = 2 (the Euclidean norm) and m = n (square matrices), the induced matrix norm is the spectral norm. The spectral norm of a matrix A is the largest singular value of A i.e. the square root of the largest eigenvalue of the positive-semidefinite matrix A*A:
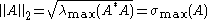
where A* denotes the conjugate transpose
Conjugate transpose
In mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...
of A.
More generally, one can define the subordinate matrix norm on
 induced by
induced by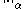 on
on 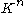 , and
, and 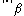 on
on 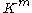 as:
as: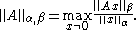
Subordinate norms are consistent with the norms that induce them, giving
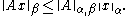
Any induced norm satisfies the inequality

where ρ(A) is the spectral radius
Spectral radius
In mathematics, the spectral radius of a square matrix or a bounded linear operator is the supremum among the absolute values of the elements in its spectrum, which is sometimes denoted by ρ.-Matrices:...
of A. For a symmetric or hermitian matrix
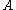 , we have equality for the 2-norm, since in this case the 2-norm is the spectral radius of
, we have equality for the 2-norm, since in this case the 2-norm is the spectral radius of 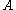 . For an arbitrary matrix, we may not have equality for any . Take
. For an arbitrary matrix, we may not have equality for any . Take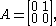
the spectral radius of
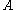 is 0, but
is 0, but 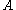 is not the zero matrix, and so none of the induced norms are equal to the spectral radius of
is not the zero matrix, and so none of the induced norms are equal to the spectral radius of 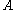 .
.Furthermore,
for square matrices
we have the spectral radius formula:
"Entrywise" norms
These vector norms treat an matrix as a vector of size
matrix as a vector of size 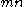 , and
, anduse one of the familiar vector norms.
For example, using the p-norm for vectors, we get:
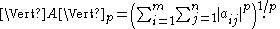
This is a different norm from the induced p-norm (see above) and the Schatten p-norm (see below), but the notation is the same.
The special case p = 2 is the Frobenius norm, and p = ∞ yields the maximum norm.
Frobenius norm
For p = 2, this is called the Frobenius norm or the Hilbert–Schmidt norm, though the latter term is often reserved for operators on Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
. This norm can be defined in various ways:
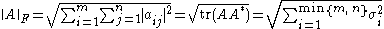
where A* denotes the conjugate transpose
Conjugate transpose
In mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...
of A, σi are the singular values of A, and the trace function is used. The Frobenius norm is very similar to the Euclidean norm on Kn and comes from an inner product on the space of all matrices.
The Frobenius norm is sub-multiplicative and is very useful for numerical linear algebra
Numerical linear algebra
Numerical linear algebra is the study of algorithms for performing linear algebra computations, most notably matrix operations, on computers. It is often a fundamental part of engineering and computational science problems, such as image and signal processing, Telecommunication, computational...
. This norm is often easier to compute than induced norms.
Max norm
The max norm is the elementwise norm with p = ∞: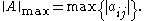
This norm is not sub-multiplicative.
Schatten norms
The Schatten p-norms arise when applying the p-norm to the vector of singular valuesSingular value decomposition
In linear algebra, the singular value decomposition is a factorization of a real or complex matrix, with many useful applications in signal processing and statistics....
of a matrix. If the singular values are denoted by σi, then the Schatten p-norm is defined by

These norms again share the notation with the induced and entrywise p-norms, but they are different.
All Schatten norms are sub-multiplicative. They are also unitarily invariant, which means that ||A|| = ||UAV|| for all matrices A and all unitary matrices U and V.
The most familiar cases are p = 1, 2, ∞. The case p = 2 yields the Frobenius norm, introduced before. The case p = ∞ yields the spectral norm, which is the matrix norm induced by the vector 2-norm (see above). Finally, p = 1 yields the nuclear norm (also known as the trace norm, or the Ky Fan 'n'-norm), defined as
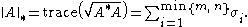
(Here
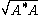 denotes a matrix
denotes a matrix  such that
such that 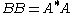 . More precisely, since
. More precisely, since 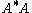 is a positive semidefinite matrix, its square root
is a positive semidefinite matrix, its square rootSquare root of a matrix
In mathematics, the square root of a matrix extends the notion of square root from numbers to matrices. A matrix B is said to be a square root of A if the matrix product B · B is equal to A.-Properties:...
is well-defined.)
Consistent norms
A matrix norm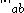 on
on  is called consistent with a vector norm
is called consistent with a vector norm 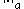 on
on 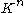 and a vector norm
and a vector norm 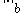 on
on 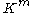 if:
if: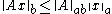
for all
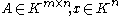 . All induced norms are consistent by definition.
. All induced norms are consistent by definition.Compatible norms
A matrix norm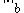 on
on 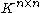 is called compatible with a vector norm
is called compatible with a vector norm 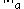 on
on 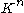 if:
if: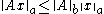
for all
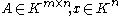 . Induced norms are compatible by definition.
. Induced norms are compatible by definition.Equivalence of norms
For any two vector norms ||·||α and ||·||β, we have
for some positive numbers r and s, for all matrices A in
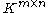 . In other words, they are equivalent norms; they induce the same topology
. In other words, they are equivalent norms; they induce the same topologyTopology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
on
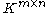 . This is a special case of the equivalence of norms in finite-dimensional Normed vector spaces.
. This is a special case of the equivalence of norms in finite-dimensional Normed vector spaces.Moreover, for every vector norm
 on
on 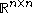 , there exists a unique positive real number
, there exists a unique positive real number 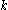 such that
such that 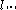 is a sub-multiplicative matrix norm for every
is a sub-multiplicative matrix norm for every 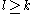 .
.A matrix norm ||·||α is said to be minimal if there exists no other matrix norm ||·||β satisfying ||·||β ≤ ||·||α.
Examples of norm equivalence
For matrix the following inequalities hold:
the following inequalities hold: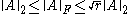 , where
, where  is the rankRank (linear algebra)The column rank of a matrix A is the maximum number of linearly independent column vectors of A. The row rank of a matrix A is the maximum number of linearly independent row vectors of A...
is the rankRank (linear algebra)The column rank of a matrix A is the maximum number of linearly independent column vectors of A. The row rank of a matrix A is the maximum number of linearly independent row vectors of A...
of
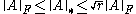 , where
, where  is the rankRank (linear algebra)The column rank of a matrix A is the maximum number of linearly independent column vectors of A. The row rank of a matrix A is the maximum number of linearly independent row vectors of A...
is the rankRank (linear algebra)The column rank of a matrix A is the maximum number of linearly independent column vectors of A. The row rank of a matrix A is the maximum number of linearly independent row vectors of A...
of
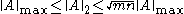
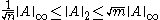
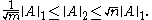
Here, ||·||p refers to the matrix norm induced by the vector p-norm.
Another useful inequality between matrix norms is