Trace class
Encyclopedia
In mathematics
, a trace class operator is a compact operator
for which a trace
may be defined, such that the trace is finite and independent of the choice of basis.
Trace class operators are essentially the same as nuclear operator
s, though many authors reserve the term "trace class operator" for the special case of nuclear operators on Hilbert space
s, and reserve nuclear (=trace class) operators for more general Banach space
s.
H is said to be in the trace class if for some (and hence all) orthonormal bases
{ek}k of H the sum of positive terms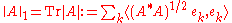
is finite.
In this case, the sum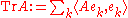
is absolutely convergent and is independent of the choice of the orthonormal basis. This value is called the trace of A. When H is finite-dimensional, every operator is trace class and this definition of trace of A coincides with the definition of the trace of a matrix.
By extension, if A is a non-negative self-adjoint operator, we can also define the trace of A as an extended real number by the
possibly divergent sum
be a trace class operator in a separable Hilbert space 
, and let
be the eigenvalues of
.
Let us assume that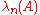
are enumerated with algebraic multiplicities taken into account
(i.e. if the algebraic multiplicity of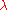
is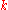
then 
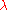is
repeated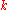
times in the list
).
Lidskii's theorem (named after Victor Borisovich Lidskii) states that
Note that the series in the left hand side converges absolutely
due to Weyl's inequality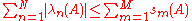
between the eigenvalues
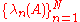and the
singular values
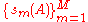
of a compact operator
.
See e.g.
s, with trace-class operators as the noncommutative analogue of the sequence space l1(N). Indeed, applying the spectral theorem
, every normal trace-class operator on a separable Hilbert space can be realized as a l1 sequence. In the same vein, the bounded operators are noncommutative versions of l∞(N), the compact operator
s that of c0 (the sequences convergent to 0), Hilbert-Schmidt operators correspond to l2(N), and finite-rank operators the sequences that have only finitely many non-zero terms. To some extent, the relationships between these classes of operators are similar to the relationships between their commutative counterparts.
Recall that every compact operator T on a Hilbert space takes the following canonical form
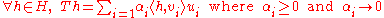
for some orthonormal bases {ui} and {vi}. Making the above heuristic comments more precise, we have that T is trace class if the series ∑i αi is convergent, T is Hilbert-Schmidt if ∑i αi2 is convergent, and T is finite rank if the sequence
{αi} has only finitely many nonzero terms.
The above description allows one to obtain easily some facts that relate these classes of operators. For example, the following inclusions hold and they are all proper when H is infinite dimensional: {finite rank} ⊂ {trace class} ⊂ {Hilbert-Schmidt} ⊂ {compact}.
The trace-class operators are given the trace norm ||T||1 = Tr [ (T*T)½ ] = ∑i αi. The norm corresponding to the Hilbert-Schmidt inner product is ||T||2 = (Tr T*T)½ = (∑iαi2)½. Also, the usual operator norm
is ||T|| = supi(αi). By classical inequalities regarding sequences,
for appropriate T.
It is also clear that finite-rank operators are dense in both trace-class and Hilbert-Schmidt in their respective norms.
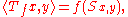
where Sx,y is the rank-one operator given by
This identification works because the finite-rank operators are norm-dense in K(H). In the event that Tf is a positive operator, for any orthonormal basis ui, one has
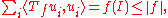
where I is the identity operator
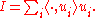
But this means Tf is trace-class. An appeal to polar decomposition extend this to the general case where Tf need not be positive.
A limiting argument via finite-rank operators shows that ||Tf ||1 = || f ||. Thus K(H)* is isometrically isomorphic to C1.
in B(H). So given any operator T in B(H), we may define a continuous linear functional
φT on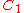
by φT(A)=Tr(AT). This correspondence between elements φT of the dual space
of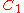
and bounded linear operators is an isometric isomorphism
. It follows that B(H) is the dual space of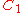
. This can be used to define the weak-* topology on B(H).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a trace class operator is a compact operator
Compact operator
In functional analysis, a branch of mathematics, a compact operator is a linear operator L from a Banach space X to another Banach space Y, such that the image under L of any bounded subset of X is a relatively compact subset of Y...
for which a trace
Trace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
may be defined, such that the trace is finite and independent of the choice of basis.
Trace class operators are essentially the same as nuclear operator
Nuclear operator
In mathematics, a nuclear operator is roughly a compact operator for which a trace may be defined, such that the trace is finite and independent of the choice of basis .Nuclear operators are essentially the same as trace class operators, though most authors reserve the term "trace...
s, though many authors reserve the term "trace class operator" for the special case of nuclear operators on Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
s, and reserve nuclear (=trace class) operators for more general Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s.
Definition
Mimicking the definition for matrices, a bounded linear operator A over a separable Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
H is said to be in the trace class if for some (and hence all) orthonormal bases
Orthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
{ek}k of H the sum of positive terms
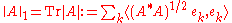
is finite.
In this case, the sum
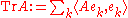
is absolutely convergent and is independent of the choice of the orthonormal basis. This value is called the trace of A. When H is finite-dimensional, every operator is trace class and this definition of trace of A coincides with the definition of the trace of a matrix.
By extension, if A is a non-negative self-adjoint operator, we can also define the trace of A as an extended real number by the
possibly divergent sum
Properties
| 1. | If A is a non-negative self-adjoint, A is trace class if and only if Tr(A) < ∞. Therefore a self adjoint operator A is trace class if and only if If and only if In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements.... its positive part A+ and negative part A− are both trace class. (The positive and negative parts of a self adjoint operator are obtained via the continuous functional calculus Continuous functional calculus In mathematics, the continuous functional calculus of operator theory and C*-algebra theory allows applications of continuous functions to normal elements of a C*-algebra. More precisely,Theorem... .) |
| 2. | The trace is a linear functional over the space of trace class operators, i.e. The bilinear map  is an inner product on the trace class; the corresponding norm is called the Hilbert-Schmidt norm. The completion of the trace class operators in the Hilbert-Schmidt norm are called the Hilbert-Schmidt operators. |
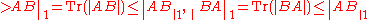| 3. | is bounded and  is trace class,  and  are also trace class and besides, under the same hypothesis,  |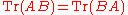
| 4. | is trace class, then one can define the determinant of  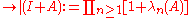 for 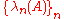 the elements of the spectrum of  ; the trace class condition on  guarantees that the infinite product is finite: indeed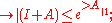 it also guarantees that  if and only if  is invertible. |
Lidskii's theorem
Let be a trace class operator in a separable Hilbert space , and let be the eigenvalues of
.Let us assume that
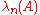
are enumerated with algebraic multiplicities taken into account
(i.e. if the algebraic multiplicity of
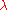
is
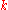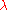then isrepeated
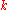times in the list).Lidskii's theorem (named after Victor Borisovich Lidskii) states that
Note that the series in the left hand side converges absolutely
due to Weyl's inequality
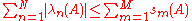
between the eigenvalues
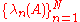and thesingular values
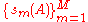
of a compact operator
.See e.g.
Relationship between some classes of operators
One can view certain classes of bounded operators as noncommutative analogue of classical sequence spaceSequence space
In functional analysis and related areas of mathematics, a sequence space is a vector space whose elements are infinite sequences of real or complex numbers. Equivalently, it is a function space whose elements are functions from the natural numbers to the field K of real or complex numbers...
s, with trace-class operators as the noncommutative analogue of the sequence space l1(N). Indeed, applying the spectral theorem
Spectral theorem
In mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized...
, every normal trace-class operator on a separable Hilbert space can be realized as a l1 sequence. In the same vein, the bounded operators are noncommutative versions of l∞(N), the compact operator
Compact operator on Hilbert space
In functional analysis, compact operators on Hilbert spaces are a direct extension of matrices: in the Hilbert spaces, they are precisely the closure of finite-rank operators in the uniform operator topology. As such, results from matrix theory can sometimes be extended to compact operators using...
s that of c0 (the sequences convergent to 0), Hilbert-Schmidt operators correspond to l2(N), and finite-rank operators the sequences that have only finitely many non-zero terms. To some extent, the relationships between these classes of operators are similar to the relationships between their commutative counterparts.
Recall that every compact operator T on a Hilbert space takes the following canonical form
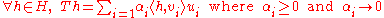
for some orthonormal bases {ui} and {vi}. Making the above heuristic comments more precise, we have that T is trace class if the series ∑i αi is convergent, T is Hilbert-Schmidt if ∑i αi2 is convergent, and T is finite rank if the sequence
{αi} has only finitely many nonzero terms.
The above description allows one to obtain easily some facts that relate these classes of operators. For example, the following inclusions hold and they are all proper when H is infinite dimensional: {finite rank} ⊂ {trace class} ⊂ {Hilbert-Schmidt} ⊂ {compact}.
The trace-class operators are given the trace norm ||T||1 = Tr [ (T*T)½ ] = ∑i αi. The norm corresponding to the Hilbert-Schmidt inner product is ||T||2 = (Tr T*T)½ = (∑iαi2)½. Also, the usual operator norm
Operator norm
In mathematics, the operator norm is a means to measure the "size" of certain linear operators. Formally, it is a norm defined on the space of bounded linear operators between two given normed vector spaces.- Introduction and definition :...
is ||T|| = supi(αi). By classical inequalities regarding sequences,
for appropriate T.
It is also clear that finite-rank operators are dense in both trace-class and Hilbert-Schmidt in their respective norms.
Trace class as the dual of compact operators
The dual space of c0 is l1(N). Similarly, we have that the dual of compact operators, denoted by K(H)*, is the trace-class operators, denoted by C1. The argument, which we now sketch, is reminiscent of that for the corresponding sequence spaces. Let f ∈ K(H)*, we identify f with the operator Tf defined by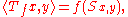where Sx,y is the rank-one operator given by
This identification works because the finite-rank operators are norm-dense in K(H). In the event that Tf is a positive operator, for any orthonormal basis ui, one has
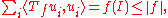
where I is the identity operator
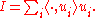
But this means Tf is trace-class. An appeal to polar decomposition extend this to the general case where Tf need not be positive.
A limiting argument via finite-rank operators shows that ||Tf ||1 = || f ||. Thus K(H)* is isometrically isomorphic to C1.
As the predual of bounded operators
Recall that the dual of l1(N) is l∞(N). In the present context, the dual of trace-class operators C1 is the bounded operators B(H). More precisely, the set C1 is a two-sided idealIdeal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
in B(H). So given any operator T in B(H), we may define a continuous linear functional
Linear functional
In linear algebra, a linear functional or linear form is a linear map from a vector space to its field of scalars. In Rn, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the dot product, or the...
φT on
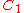by φT(A)=Tr(AT). This correspondence between elements φT of the dual spaceDual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
of
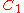and bounded linear operators is an isometric isomorphismIsomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
. It follows that B(H) is the dual space of
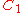. This can be used to define the weak-* topology on B(H).