
Generalized singular value decomposition
Encyclopedia
In linear algebra
the generalized singular value decomposition (GSVD) is a matrix decomposition
more general than the singular value decomposition
. It is used to study the conditioning
and regularization
of linear systems with respect to quadratic semi-norms.
Given an matrix
matrix  and a
and a 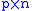 matrix
matrix  of real or complex numbers the GSVD is
of real or complex numbers the GSVD is
and
where and
and  are unitary matrices and
are unitary matrices and  is an upper triangular, nonsingular
is an upper triangular, nonsingular  matrix, and
matrix, and  is the rank of
is the rank of 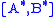 . Also,
. Also,
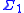 and
and  are
are  and
and  matrices, zero except for the leading diagonals which consist of the real numbers
matrices, zero except for the leading diagonals which consist of the real numbers 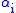 and
and  respectively, satisfying
respectively, satisfying
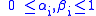 and
and 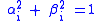 .
.
The ratios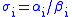 are analogous to the singular values. In the important special case, where
are analogous to the singular values. In the important special case, where  is square and invertible, they are the singular values, and
is square and invertible, they are the singular values, and  and
and  are the matrices of singular vectors, of the matrix
are the matrices of singular vectors, of the matrix 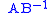 .
.
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
the generalized singular value decomposition (GSVD) is a matrix decomposition
Matrix decomposition
In the mathematical discipline of linear algebra, a matrix decomposition is a factorization of a matrix into some canonical form. There are many different matrix decompositions; each finds use among a particular class of problems.- Example :...
more general than the singular value decomposition
Singular value decomposition
In linear algebra, the singular value decomposition is a factorization of a real or complex matrix, with many useful applications in signal processing and statistics....
. It is used to study the conditioning
Condition number
In the field of numerical analysis, the condition number of a function with respect to an argument measures the asymptotically worst case of how much the function can change in proportion to small changes in the argument...
and regularization
Regularization (mathematics)
In mathematics and statistics, particularly in the fields of machine learning and inverse problems, regularization involves introducing additional information in order to solve an ill-posed problem or to prevent overfitting...
of linear systems with respect to quadratic semi-norms.
Given an
 matrix
matrix  and a
and a 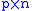 matrix
matrix  of real or complex numbers the GSVD is
of real or complex numbers the GSVD is
and

where
 and
and  are unitary matrices and
are unitary matrices and  is an upper triangular, nonsingular
is an upper triangular, nonsingular  matrix, and
matrix, and  is the rank of
is the rank of 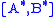 . Also,
. Also,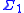 and
and  are
are  and
and  matrices, zero except for the leading diagonals which consist of the real numbers
matrices, zero except for the leading diagonals which consist of the real numbers 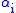 and
and  respectively, satisfying
respectively, satisfying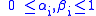 and
and 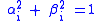 .
.The ratios
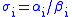 are analogous to the singular values. In the important special case, where
are analogous to the singular values. In the important special case, where  is square and invertible, they are the singular values, and
is square and invertible, they are the singular values, and  and
and  are the matrices of singular vectors, of the matrix
are the matrices of singular vectors, of the matrix 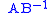 .
.

