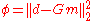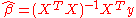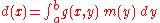Inverse problem
Encyclopedia
An inverse problem is a general framework that is used to convert observed measurements into information about a physical object or system that we are interested in. For example, if we have measurements of the Earth's gravity field, then we might ask the question: "given the data that we have available, what can we say about the density distribution of the Earth in that area?" The solution to this problem (i.e. the density distribution that best matches the data) is useful because it generally tells us something about a physical parameter that we cannot directly observe. Thus, inverse problems are one of the most important, and well-studied mathematical problems in science
and mathematics
. Inverse problems arise in many branches of science
and mathematics
, including: computer vision
, machine learning
, statistics
, statistical inference
, geophysics
, medical imaging
(such as computed axial tomography and EEG
/ERP), remote sensing
, ocean acoustic tomography
, nondestructive testing
, astronomy
, physics
and many other fields.
-Armenian
physicist, Viktor Ambartsumian.
While still a student, Ambartsumian thoroughly studied the theory of atomic structure, the formation of energy levels, and the Schrödinger equation
and its properties, and when he mastered the theory of eigenvalues of differential equation
s, he pointed out the apparent analogy between discrete energy levels and the eigenvalues of differential equations. He then asked: given a family of eigenvalues, is it possible to find the form of the equations whose eigenvalues they are? Essentially Ambartsumian was examining the inverse Sturm–Liouville problem, which dealt with determining the equations of a vibrating string. This paper was published in 1929 in the German physics journal Zeitschrift für Physik
and remained in oblivion for a rather long time. Describing this situation after many decades, Ambartsumian said, "If an astronomer publishes an article with a mathematical content in a physics journal, then the most likely thing that will happen to it is oblivion."
Nonetheless, toward the end of the Second World War, this article, written by the 20-year-old Ambartsumian, was found by Swedish mathematicians and formed the starting point for a whole area of research on inverse problems, becoming the foundation of an entire discipline.
The inverse problem is considered the "inverse" to the forward problem which relates the model parameters to the data that we observe:
The transformation from data to model parameters (or vice versa) is a result of the interaction of a physical system with the object that we wish to infer properties about. In other words, the transformation is the physics that relates the physical quantity (i.e. the model parameters) to the observed data.
The table below shows some examples of: physical systems, the governing physics, the physical quantity that we are interested, and what we actually observe.
Linear algebra is useful in understanding the physical and mathematical construction of inverse problems, because of the presence of the transformation or "mapping" of data to the model parameters.
 , such that (at least approximately)
, such that (at least approximately)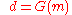
where is an operator describing the explicit relationship between the observed data,
is an operator describing the explicit relationship between the observed data, 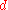 , and the model parameters. In various contexts, the operator
, and the model parameters. In various contexts, the operator  is called forward operator, observation operator, or observation function. In the most general context, G represents the governing equations that relate the model parameters to the observed data (i.e. the governing physics).
is called forward operator, observation operator, or observation function. In the most general context, G represents the governing equations that relate the model parameters to the observed data (i.e. the governing physics).
,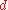 and
and  are vectors, and the problem can be written as
are vectors, and the problem can be written as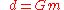
where is a matrix
is a matrix
, often called the observation matrix.
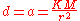
where is a measure of the local gravitational acceleration,
is a measure of the local gravitational acceleration,  is the universal gravitational constant,
is the universal gravitational constant,  is the local mass (density) of the rock in the subsurface and
is the local mass (density) of the rock in the subsurface and  is the distance from the mass to the observation point.
is the distance from the mass to the observation point.
By discretizing the above expression, we are able to relate the discrete data observations on the surface of the Earth to the discrete model parameters (density) in the subsurface that we wish to know more about. For example, consider the case where we have 5 measurements on the surface of the Earth. In this case, our data vector, d is a column vector of dimension (5x1). We also know that we only have five unknown masses in the subsurface (unrealistic but used to demonstrate the concept). Thus, we can construct the linear system relating the five unknown masses to the five data points as follows:
Science
Science is a systematic enterprise that builds and organizes knowledge in the form of testable explanations and predictions about the universe...
and mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
. Inverse problems arise in many branches of science
Science
Science is a systematic enterprise that builds and organizes knowledge in the form of testable explanations and predictions about the universe...
and mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, including: computer vision
Computer vision
Computer vision is a field that includes methods for acquiring, processing, analysing, and understanding images and, in general, high-dimensional data from the real world in order to produce numerical or symbolic information, e.g., in the forms of decisions...
, machine learning
Machine learning
Machine learning, a branch of artificial intelligence, is a scientific discipline concerned with the design and development of algorithms that allow computers to evolve behaviors based on empirical data, such as from sensor data or databases...
, statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, statistical inference
Statistical inference
In statistics, statistical inference is the process of drawing conclusions from data that are subject to random variation, for example, observational errors or sampling variation...
, geophysics
Geophysics
Geophysics is the physics of the Earth and its environment in space; also the study of the Earth using quantitative physical methods. The term geophysics sometimes refers only to the geological applications: Earth's shape; its gravitational and magnetic fields; its internal structure and...
, medical imaging
Medical imaging
Medical imaging is the technique and process used to create images of the human body for clinical purposes or medical science...
(such as computed axial tomography and EEG
Electroencephalography
Electroencephalography is the recording of electrical activity along the scalp. EEG measures voltage fluctuations resulting from ionic current flows within the neurons of the brain...
/ERP), remote sensing
Remote sensing
Remote sensing is the acquisition of information about an object or phenomenon, without making physical contact with the object. In modern usage, the term generally refers to the use of aerial sensor technologies to detect and classify objects on Earth by means of propagated signals Remote sensing...
, ocean acoustic tomography
Ocean acoustic tomography
Ocean Acoustic Tomography is a technique used to measure temperatures and currents over large regions of the ocean. On ocean basin scales, this technique is also known as acoustic thermometry. The technique relies on precisely measuring the time it takes sound signals to travel between two...
, nondestructive testing
Nondestructive testing
Nondestructive testing or Non-destructive testing is a wide group of analysis techniques used in science and industry to evaluate the properties of a material, component or system without causing damage....
, astronomy
Astronomy
Astronomy is a natural science that deals with the study of celestial objects and phenomena that originate outside the atmosphere of Earth...
, physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
and many other fields.
History
The field of inverse problems was first discovered and introduced by SovietSoviet Union
The Soviet Union , officially the Union of Soviet Socialist Republics , was a constitutionally socialist state that existed in Eurasia between 1922 and 1991....
-Armenian
Armenians
Armenian people or Armenians are a nation and ethnic group native to the Armenian Highland.The largest concentration is in Armenia having a nearly-homogeneous population with 97.9% or 3,145,354 being ethnic Armenian....
physicist, Viktor Ambartsumian.
While still a student, Ambartsumian thoroughly studied the theory of atomic structure, the formation of energy levels, and the Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
and its properties, and when he mastered the theory of eigenvalues of differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s, he pointed out the apparent analogy between discrete energy levels and the eigenvalues of differential equations. He then asked: given a family of eigenvalues, is it possible to find the form of the equations whose eigenvalues they are? Essentially Ambartsumian was examining the inverse Sturm–Liouville problem, which dealt with determining the equations of a vibrating string. This paper was published in 1929 in the German physics journal Zeitschrift für Physik
Zeitschrift für Physik
The European Physical Journal is a joint publication of EDP Sciences, Springer Science+Business Media, and the Società Italiana di Fisica...
and remained in oblivion for a rather long time. Describing this situation after many decades, Ambartsumian said, "If an astronomer publishes an article with a mathematical content in a physics journal, then the most likely thing that will happen to it is oblivion."
Nonetheless, toward the end of the Second World War, this article, written by the 20-year-old Ambartsumian, was found by Swedish mathematicians and formed the starting point for a whole area of research on inverse problems, becoming the foundation of an entire discipline.
Conceptual understanding
The inverse problem can be conceptually formulated as follows:- Data → Model parameters
The inverse problem is considered the "inverse" to the forward problem which relates the model parameters to the data that we observe:
- Model parameters → Data
The transformation from data to model parameters (or vice versa) is a result of the interaction of a physical system with the object that we wish to infer properties about. In other words, the transformation is the physics that relates the physical quantity (i.e. the model parameters) to the observed data.
The table below shows some examples of: physical systems, the governing physics, the physical quantity that we are interested, and what we actually observe.
| Physical system | Governing equations | Physical quantity | Observed data |
|---|---|---|---|
| Earth's gravitational field | Newton's law of gravity Newton's law of universal gravitation Newton's law of universal gravitation states that every point mass in the universe attracts every other point mass with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between them... |
Density | Gravitational field Gravitational field The gravitational field is a model used in physics to explain the existence of gravity. In its original concept, gravity was a force between point masses... |
| Earth's magnetic field (at the surface) | Maxwell's equations Maxwell's equations Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations... |
Magnetic susceptibility Magnetic susceptibility In electromagnetism, the magnetic susceptibility \chi_m is a dimensionless proportionality constant that indicates the degree of magnetization of a material in response to an applied magnetic field... |
Magnetic field Magnetic field A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;... |
| Seismic wave Seismic wave Seismic waves are waves of energy that travel through the earth, and are a result of an earthquake, explosion, or a volcano that imparts low-frequency acoustic energy. Many other natural and anthropogenic sources create low amplitude waves commonly referred to as ambient vibrations. Seismic waves... s (from earthquakes) |
Wave equation Wave equation The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics... |
Wave-speed (density) | Particle velocity Particle velocity Particle velocity is the velocity v of a particle in a medium as it transmits a wave. In many cases this is a longitudinal wave of pressure as with sound, but it can also be a transverse wave as with the vibration of a taut string.... |
Linear algebra is useful in understanding the physical and mathematical construction of inverse problems, because of the presence of the transformation or "mapping" of data to the model parameters.
General statement of the problem
The objective of an inverse problem is to find the best model, , such that (at least approximately)
, such that (at least approximately)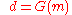
where
 is an operator describing the explicit relationship between the observed data,
is an operator describing the explicit relationship between the observed data, 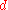 , and the model parameters. In various contexts, the operator
, and the model parameters. In various contexts, the operator  is called forward operator, observation operator, or observation function. In the most general context, G represents the governing equations that relate the model parameters to the observed data (i.e. the governing physics).
is called forward operator, observation operator, or observation function. In the most general context, G represents the governing equations that relate the model parameters to the observed data (i.e. the governing physics).Linear inverse problems
In the case of a discrete linear inverse problem describing a linear systemLinear system
A linear system is a mathematical model of a system based on the use of a linear operator.Linear systems typically exhibit features and properties that are much simpler than the general, nonlinear case....
,
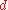 and
and  are vectors, and the problem can be written as
are vectors, and the problem can be written as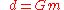
where
 is a matrix
is a matrixMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
, often called the observation matrix.
Earth's gravitational field
Only a few physical systems are actually linear with respect to the model parameters. One such system from geophysics is that of the Earth's gravitational field. The Earth's gravitational field is determined by the density distribution of the Earth in the subsurface. Because the lithology of the Earth changes quite significantly, we are able to observe minute differences in the Earth's gravitational field on the surface of the Earth. From our understanding of gravity (Newton's Law of Gravitation), we know that the mathematical expression for gravity is: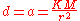
where
 is a measure of the local gravitational acceleration,
is a measure of the local gravitational acceleration,  is the universal gravitational constant,
is the universal gravitational constant,  is the local mass (density) of the rock in the subsurface and
is the local mass (density) of the rock in the subsurface and  is the distance from the mass to the observation point.
is the distance from the mass to the observation point.By discretizing the above expression, we are able to relate the discrete data observations on the surface of the Earth to the discrete model parameters (density) in the subsurface that we wish to know more about. For example, consider the case where we have 5 measurements on the surface of the Earth. In this case, our data vector, d is a column vector of dimension (5x1). We also know that we only have five unknown masses in the subsurface (unrealistic but used to demonstrate the concept). Thus, we can construct the linear system relating the five unknown masses to the five data points as follows:
-

-

-
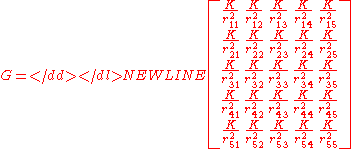
Now, we can see that the system has five equations, , with five unknowns,
, with five unknowns,  . To solve for the model parameters that fit our data, we might be able to invert the matrix
. To solve for the model parameters that fit our data, we might be able to invert the matrix  to directly convert the measurements into our model parameters. For example:
to directly convert the measurements into our model parameters. For example:
However, not all square matrices are invertible ( is almost never invertible). This is because we are not guaranteed to have enough information to uniquely determine the solution to the given equations unless we have independent measurements (i.e. each measurement adds unique information to the system). It's important to note that in most physical systems, we do not ever have enough information to uniquely constrain our solutions because the observation matrix does not contain unique equations. From a linear algebra perspective, the matrix
is almost never invertible). This is because we are not guaranteed to have enough information to uniquely determine the solution to the given equations unless we have independent measurements (i.e. each measurement adds unique information to the system). It's important to note that in most physical systems, we do not ever have enough information to uniquely constrain our solutions because the observation matrix does not contain unique equations. From a linear algebra perspective, the matrix  is rank deficient (i.e. has zero eigenvalues), meaning that is not invertible. Further, if we add additional observations to our matrix (i.e. more equations), then the matrix
is rank deficient (i.e. has zero eigenvalues), meaning that is not invertible. Further, if we add additional observations to our matrix (i.e. more equations), then the matrix  is no longer square. Even then, we're not guaranteed to have full-rank in the observation matrix. Therefore, most inverse problems are considered to be underdetermined, meaning that we do not have unique solutions to the inverse problem. If we have a full-rank system, then our solution may be unique. Overdetermined systems (more equations than unknowns) have other issues.
is no longer square. Even then, we're not guaranteed to have full-rank in the observation matrix. Therefore, most inverse problems are considered to be underdetermined, meaning that we do not have unique solutions to the inverse problem. If we have a full-rank system, then our solution may be unique. Overdetermined systems (more equations than unknowns) have other issues.
Because we cannot directly invert the observation matrix, we use methods from optimization to solve the inverse problem. To do so, we define a goal, also known as an objective function, for the inverse problem. The goal is a functionalFunctional (mathematics)In mathematics, and particularly in functional analysis, a functional is a map from a vector space into its underlying scalar field. In other words, it is a function that takes a vector as its input argument, and returns a scalar...
that measures how close the predicted data from the recovered model fits the observed data. In the case where we have perfect data (i.e. no noise) and perfect physical understanding (i.e. we know the physics) then the recovered model should fit the observed data perfectly. The standard objective function, , is usually of the form:
, is usually of the form:
which represents the L-2 norm of the misfit between the observed data and the predicted data from the model. We use the L-2 norm here as a generic measurement of the distance between the predicted data and the observed data, but other norms are possible for use. The goal of the objective function is to minimize the difference between the predicted and observed data.
To minimize the objective function (i.e. solve the inverse problem) we compute the gradient of the objective function using the same rationale as we would to minimize a function of only one variable. The gradient of the objective function is:
Which simplifies to:
After rearrangement, this becomes:
This expression is known as the Normal Equations and gives us a possible solution to the inverse problem. This is equivalent to Ordinary Least SquaresOrdinary least squaresIn statistics, ordinary least squares or linear least squares is a method for estimating the unknown parameters in a linear regression model. This method minimizes the sum of squared vertical distances between the observed responses in the dataset and the responses predicted by the linear...
Additionally, we usually know that our data has random variations caused by random noise, or worse yet coherent noise. In any case, errors in the observed data introduces errors in the recovered model parameters that we obtain by solving the inverse problem. To avoid these errors, we may want to constrain possible solutions to emphasize certain possible features in our models. This type of constraint is known as regularization.
Mathematical
One central example of a linear inverse problem is provided by a FredholmFredholm integral equationIn mathematics, the Fredholm integral equation is an integral equation whose solution gives rise to Fredholm theory, the study of Fredholm kernels and Fredholm operators. The integral equation was studied by Ivar Fredholm.-Equation of the first kind :...
first kind integral equationIntegral equationIn mathematics, an integral equation is an equation in which an unknown function appears under an integral sign. There is a close connection between differential and integral equations, and some problems may be formulated either way...
.
For sufficiently smooth the operator defined above is compactCompact operatorIn functional analysis, a branch of mathematics, a compact operator is a linear operator L from a Banach space X to another Banach space Y, such that the image under L of any bounded subset of X is a relatively compact subset of Y...
the operator defined above is compactCompact operatorIn functional analysis, a branch of mathematics, a compact operator is a linear operator L from a Banach space X to another Banach space Y, such that the image under L of any bounded subset of X is a relatively compact subset of Y...
on reasonable Banach spaceBanach spaceIn mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s such as Lp spaceLp spaceIn mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
s. Even if the mapping is injectiveInjective functionIn mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
its inverseInverse functionIn mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
will not be continuous. (However, by the bounded inverse theorem, if the mapping is bijective, then the inverse will be bounded (i.e. continuous).) Thus small errors in the data are greatly amplified in the solution
are greatly amplified in the solution  . In this sense the inverse problem of inferring
. In this sense the inverse problem of inferring  from measured
from measured 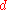 is ill-posed.
is ill-posed.
To obtain a numerical solution, the integral must be approximated using quadratureNumerical integrationIn numerical analysis, numerical integration constitutes a broad family of algorithms for calculating the numerical value of a definite integral, and by extension, the term is also sometimes used to describe the numerical solution of differential equations. This article focuses on calculation of...
, and the data sampled at discrete points. The resulting system of linear equations will be ill-conditionedCondition numberIn the field of numerical analysis, the condition number of a function with respect to an argument measures the asymptotically worst case of how much the function can change in proportion to small changes in the argument...
.
Another example is the inversion of the Radon transformRadon transformthumb|right|Radon transform of the [[indicator function]] of two squares shown in the image below. Lighter regions indicate larger function values. Black indicates zero.thumb|right|Original function is equal to one on the white region and zero on the dark region....
. Here a function (for example of two variables) is deduced from its integrals along all possible lines. This is precisely the problem solved in image reconstruction for X-rayX-rayX-radiation is a form of electromagnetic radiation. X-rays have a wavelength in the range of 0.01 to 10 nanometers, corresponding to frequencies in the range 30 petahertz to 30 exahertz and energies in the range 120 eV to 120 keV. They are shorter in wavelength than UV rays and longer than gamma...
computerized tomography. Although from a theoretical point of view many linear inverse problems are well understood, problems involving the Radon transform and its generalisations still present many theoretical challenges with questions of sufficiency of data still unresolved. Such problems include incomplete data for the x-ray transform in three dimensions and problems involving the generalisation of the x-ray transform to tensor fields.
A final example related to the Riemann HypothesisRiemann hypothesisIn mathematics, the Riemann hypothesis, proposed by , is a conjecture about the location of the zeros of the Riemann zeta function which states that all non-trivial zeros have real part 1/2...
was given by Wu and Sprung, the idea is that in the Semiclassical (old) Quantum theory the inverse of the potential inside the Hamiltonian is proportional to the half-derivative of the eigenvalues (energies) counting function n(x)
Non-linear inverse problems
An inherently more difficult family of inverse problems are collectively referred to as non-linear inverse problems.
Non-linear inverse problems have a more complex relationship between data and model, represented by the equation:

Here is a non-linear operator and cannot be separated to represent a linear mapping of the model parameters that form
is a non-linear operator and cannot be separated to represent a linear mapping of the model parameters that form  into the data. In such research, the first priority is to understand the structure of the problem and to give a theoretical answer to the three Hadamard questions (so that the problem is solved from the theoretical point of view). It is only later in a study that regularization and interpretation of the solution's (or solutions', depending upon conditions of uniqueness) dependence upon parameters and data/measurements (probabilistic ones or others) can be done. Hence the corresponding following sections do not really apply to these problems. Whereas linear inverse problems were completely solved from the theoretical point of view at the end of the nineteenth century, only one class of nonlinear inverse problems was so before 1970, that of inverse spectral and (one space dimension) inverse scattering problems, after the seminal work of the Russian mathematical school (KreinMark Grigoryevich KreinMark Grigorievich Krein was a Soviet Jewish mathematician, one of the major figures of the Soviet school of functional analysis. He is known for works in operator theory , the problem of moments, classical analysis and representation theory.He was born in Kiev, leaving home at age 17 to go to...
into the data. In such research, the first priority is to understand the structure of the problem and to give a theoretical answer to the three Hadamard questions (so that the problem is solved from the theoretical point of view). It is only later in a study that regularization and interpretation of the solution's (or solutions', depending upon conditions of uniqueness) dependence upon parameters and data/measurements (probabilistic ones or others) can be done. Hence the corresponding following sections do not really apply to these problems. Whereas linear inverse problems were completely solved from the theoretical point of view at the end of the nineteenth century, only one class of nonlinear inverse problems was so before 1970, that of inverse spectral and (one space dimension) inverse scattering problems, after the seminal work of the Russian mathematical school (KreinMark Grigoryevich KreinMark Grigorievich Krein was a Soviet Jewish mathematician, one of the major figures of the Soviet school of functional analysis. He is known for works in operator theory , the problem of moments, classical analysis and representation theory.He was born in Kiev, leaving home at age 17 to go to...
, GelfandIsrael GelfandIsrael Moiseevich Gelfand, also written Israïl Moyseyovich Gel'fand, or Izrail M. Gelfand was a Soviet mathematician who made major contributions to many branches of mathematics, including group theory, representation theory and functional analysis...
, Levitan, MarchenkoVladimir MarchenkoVladimir Marchenko is a Ukrainian mathematician who specializes in mathematical physics, in particular in the analysis of the Sturm–Liouville operators. He introduced one of the approaches to the inverse problem for Sturm–Liouville operators...
). A large review of the results has been given by Chadan and Sabatier in their book "Inverse Problems of Quantum Scattering Theory" (two editions in English, one in Russian).
In this kind of problem, data are properties of the spectrum of a linear operator which describe the scattering. The spectrum is made of eigenvalues and eigenfunctionEigenfunctionIn mathematics, an eigenfunction of a linear operator, A, defined on some function space is any non-zero function f in that space that returns from the operator exactly as is, except for a multiplicative scaling factor. More precisely, one has...
s, forming together the "discrete spectrum", and generalizations, called the continuous spectrum. The very remarkable physical point is that scattering experiments give information only on the continuous spectrum, and that knowing its full spectrum is both necessary and sufficient in recovering the scattering operator. Hence we have invisible parameters, much more interesting than the null space which has a similar property in linear inverse problems. In addition, there are physical motions in which the spectrum of such an operator is conserved as a consequence of such motion. This phenomenon is governed by special nonlinear partial differential evolution equations, for example the Korteweg–de Vries equationKorteweg–de Vries equationIn mathematics, the Korteweg–de Vries equation is a mathematical model of waves on shallow water surfaces. It is particularly notable as the prototypical example of an exactly solvable model, that is, a non-linear partial differential equation whose solutions can be exactly and precisely specified...
. If the spectrum of the operator is reduced to one single eigenvalue, its corresponding motion is that of a single bump that propagates at constant velocity and without deformation, a solitary wave called a "solitonSolitonIn mathematics and physics, a soliton is a self-reinforcing solitary wave that maintains its shape while it travels at constant speed. Solitons are caused by a cancellation of nonlinear and dispersive effects in the medium...
".
A perfect signal and its generalizations for the Korteweg–de Vries equation or other integrable nonlinear partial differential equations are of great interest, with many possible applications. This area has been studied as a branch of mathematical physics since the 1970s. Nonlinear inverse problems are also currently studied in many fields of applied science (acoustics, mechanics, quantum mechanics, electromagnetic scattering - in particular radar soundings, seismic soundings and nearly all imaging modalities).
Mathematical considerations
Inverse problems are typically ill posed, as opposed to the well-posed problemWell-posed problemThe mathematical term well-posed problem stems from a definition given by Jacques Hadamard. He believed that mathematical models of physical phenomena should have the properties that# A solution exists# The solution is unique...
s more typical when modeling physical situations where the model parameters or material properties are known. Of the three conditions for a well-posed problemWell-posed problemThe mathematical term well-posed problem stems from a definition given by Jacques Hadamard. He believed that mathematical models of physical phenomena should have the properties that# A solution exists# The solution is unique...
suggested by Jacques HadamardJacques HadamardJacques Salomon Hadamard FRS was a French mathematician who made major contributions in number theory, complex function theory, differential geometry and partial differential equations.-Biography:...
(existence, uniqueness, stability of the solution or solutions) the condition of stability is most often violated. In the sense of functional analysisFunctional analysisFunctional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, the inverse problem is represented by a mapping between metric spaceMetric spaceIn mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
s. While inverse problems are often formulated in infinite dimensional spaces, limitations to a finite number of measurements, and the practical consideration of recovering only a finite number of unknown parameters, may lead to the problems being recast in discrete form. In this case the inverse problem will typically be ill-conditionedCondition numberIn the field of numerical analysis, the condition number of a function with respect to an argument measures the asymptotically worst case of how much the function can change in proportion to small changes in the argument...
. In these cases, regularizationRegularization (mathematics)In mathematics and statistics, particularly in the fields of machine learning and inverse problems, regularization involves introducing additional information in order to solve an ill-posed problem or to prevent overfitting...
may be used to introduce mild assumptions on the solution and prevent overfittingOverfittingIn statistics, overfitting occurs when a statistical model describes random error or noise instead of the underlying relationship. Overfitting generally occurs when a model is excessively complex, such as having too many parameters relative to the number of observations...
. Many instances of regularized inverse problems can be interpreted as special cases of Bayesian inferenceBayesian inferenceIn statistics, Bayesian inference is a method of statistical inference. It is often used in science and engineering to determine model parameters, make predictions about unknown variables, and to perform model selection...
.
Inverse problems societies
See also
- Data assimilationData assimilationApplications of data assimilation arise in many fields of geosciences, perhaps most importantly in weather forecasting and hydrology. Data assimilation proceeds by analysis cycles...
- Mathematical geophysicsMathematical geophysicsMathematical geophysics is concerned with developing mathematical methods for use in geophysics. As such, it has application in many fields in geophysics, particularly geodynamics and seismology.- Geophysical fluid dynamics :...
- Tikhonov regularizationTikhonov regularizationTikhonov regularization, named for Andrey Tikhonov, is the most commonly used method of regularization of ill-posed problems. In statistics, the method is known as ridge regression, and, with multiple independent discoveries, it is also variously known as the Tikhonov-Miller method, the...
- Backus–Gilbert methodBackus–Gilbert methodIn mathematics, the Backus–Gilbert method, also known as the optimally localized average method is named for its discoverers, geophysicists George E. Backus and James Freeman Gilbert. It is a regularization method for obtaining meaningful solutions to ill-posed inverse problems...
External links
- Inverse Problems Network
- Inverse Problems page at the University of Alabama
- Albert Tarantola's website, including a free PDF version of his Inverse Problem Theory book, and some on-line articles on Inverse Problems
- Andy Ganse's Geophysical Inverse Theory Resources Page
- Finnish Centre of Excellence in Inverse Problems Research
Academic journals
There are four main academic journals covering inverse problems in general.- Inverse Problems
- Journal of Inverse and Ill-posed Problems
- Inverse Problems in Science and Engineering
- Inverse Problems and Imaging
In addition there are many journals on medical imaging, geophysics, non-destructive testing etc. that are dominated by inverse problems in those areas. -
-
-