
Locality sensitive hashing
Encyclopedia
Locality-sensitive hashing (LSH) is a method of performing probabilistic dimension reduction of high-dimensional data. The basic idea is to hash
the input items so that similar items are mapped to the same buckets with high probability (the number of buckets being much smaller than the universe of possible input items).
 is defined for
is defined for
a metric space
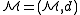 , a threshold
, a threshold
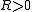 and an approximation factor
and an approximation factor 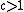 .
.
An LSH family
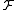 is a family of functions
is a family of functions 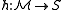 satisfying the following conditions for any two points
satisfying the following conditions for any two points 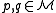 , and a function
, and a function 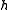 chosen uniformly at random from
chosen uniformly at random from 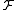 :
:
A family is interesting when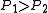 . Such a family
. Such a family 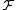 is called
is called  -sensitive.
-sensitive.
An alternative definition is defined with respect to a universe of items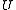 that have a similarity
that have a similarity
function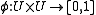 . An LSH scheme is a family of hash function
. An LSH scheme is a family of hash function
s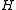 coupled with a probability distribution
coupled with a probability distribution 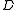 over the functions such that a function
over the functions such that a function  chosen according to
chosen according to 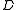 satisfies the property that
satisfies the property that 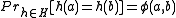 for any
for any 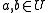 .
.
This approach works for the Hamming distance
over d-dimensional vectors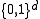 . Here, the family
. Here, the family 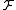 of hash functions is simply the family of all the projections of points on
of hash functions is simply the family of all the projections of points on
one of the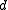 coordinates, i.e.,
coordinates, i.e., 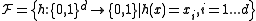 ,
,
where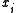 is the
is the 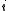 th coordinate of
th coordinate of
 . A random function
. A random function 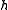 from
from 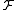 simply selects a random bit from the input point. This family has the following parameters:
simply selects a random bit from the input point. This family has the following parameters:
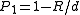 ,
, 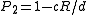 .
.
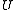 is composed of subsets of some ground set of enumerable items
is composed of subsets of some ground set of enumerable items 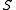 and the similarity function of interest is the Jaccard index
and the similarity function of interest is the Jaccard index
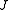 . If
. If  is a permutation on the indices of
is a permutation on the indices of 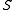 , for
, for  let
let 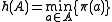 . Each possible choice of
. Each possible choice of  defines a single hash function
defines a single hash function 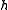 mapping input sets to integers.
mapping input sets to integers.
Define the function family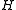 to be the set of all such functions and let
to be the set of all such functions and let 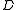 be the uniform distribution. Given two sets
be the uniform distribution. Given two sets 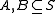 the event that
the event that 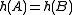 corresponds exactly to the event that the minimizer of
corresponds exactly to the event that the minimizer of  lies inside
lies inside 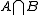 . As
. As 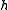 was chosen uniformly at random,
was chosen uniformly at random, 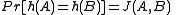 and
and 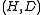 define an LSH scheme for the Jaccard index.
define an LSH scheme for the Jaccard index.
Because the symmetric group on n elements has size n!, choosing a truly random permutation from the full symmetric group is infeasible for even moderately sized n. Because of this fact, there has been significant work on finding a family of permutations that is "min-wise independent" - a permutation family for which each element of the domain has equal probability of being the minimum under a randomly chosen . It has been established that a min-wise independent family of permutations is at least of size
. It has been established that a min-wise independent family of permutations is at least of size 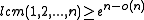 . and that this boundary is tight
. and that this boundary is tight
Because min-wise independent families are too big for practical applications, two variant notions of min-wise independence are introduced: restricted min-wise independent permutations families, and approximate min-wise independent families.
Restricted min-wise independence is the min-wise independence property restricted to certain sets of cardinality at most k .
Approximate min-wise independence differs from the property by at most a fixed .
.
(defined by a normal unit vector ) at the outset and use the hyperplane to hash input vectors.
) at the outset and use the hyperplane to hash input vectors.
Given an input vector and a hyperplane defined by
and a hyperplane defined by  , we let
, we let 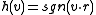 . That is,
. That is, 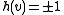 depending on which side of the hyperplane
depending on which side of the hyperplane  lies.
lies.
Each possible choice of defines a single function. Let
defines a single function. Let  be the set of all such functions and let
be the set of all such functions and let 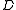 be the uniform distribution once again. It is not difficult to prove that, for two vectors
be the uniform distribution once again. It is not difficult to prove that, for two vectors 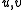 ,
, 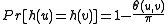 , where
, where 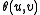 is the angle between
is the angle between  and
and  .
. 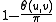 is closely related to
is closely related to 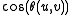 .
.
In this instance hashing produces only a single bit. Two vectors' bits match with probability proportional to the cosine of the angle between them.
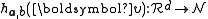 maps a d dimensional vector
maps a d dimensional vector
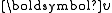 onto a set of integers. Each hash function
onto a set of integers. Each hash function
in the family is indexed by a choice of random and
and
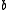 where
where  is a d dimensional
is a d dimensional
vector with
entries chosen independently from a stable distribution and
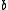 is
is
a real number chosen uniformly from the range [0,r]. For a fixed
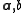 the hash function
the hash function 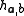 is
is
given by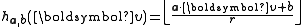 .
.
Other construction methods for hash functions have been proposed to better fit the data.
In particular k-means hash functions are better in practice than projection-based hash functions, but without any theoretical guarantee.
algorithms.
Consider any LSH family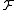 . The
. The
algorithm has two main parameters: the width parameter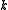 and the
and the
number of hash tables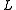 .
.
In the first step, we define a new family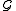 of hash
of hash
functions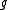 , where each function
, where each function 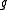 is
is
obtained by concatenating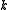 functions
functions
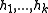 from
from
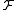 , i.e.,
, i.e., 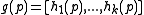 .
.
In other words, a random hash function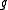 is obtained by
is obtained by
concatenating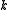 randomly chosen hash functions from
randomly chosen hash functions from
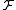 .
.
The algorithm then constructs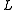 hash tables, each
hash tables, each
corresponding to
a different randomly chosen hash function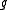 .
.
In the preprocessing step we hash all points from the data set
points from the data set
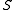 into each of
into each of
the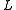 hash tables.
hash tables.
Given that the resulting hash tables have only non-zero
non-zero
entries,
one can reduce the amount of memory used per each hash table to
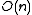 using standard hash functions.
using standard hash functions.
Given a query point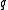 , the algorithm iterates over the
, the algorithm iterates over the
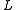 hash functions
hash functions 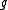 .
.
For each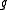 considered, it retrieves the data points that
considered, it retrieves the data points that
are hashed
into the same bucket as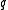 .
.
The process is stopped as soon as a point within distance from
from
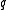 is found.
is found.
Given the parameters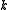 and
and 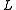 , the algorithm has
, the algorithm has
the following performance guarantees:
For a fixed approximation ratio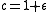 and probabilities
and probabilities
 and
and 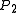 , one can set
, one can set 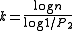 and
and 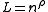 , where
, where
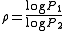 .
.
Then one obtains the following performance guarantees:
Hash function
A hash function is any algorithm or subroutine that maps large data sets to smaller data sets, called keys. For example, a single integer can serve as an index to an array...
the input items so that similar items are mapped to the same buckets with high probability (the number of buckets being much smaller than the universe of possible input items).
Definition
An LSH family is defined for
is defined fora metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
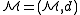 , a threshold
, a threshold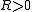 and an approximation factor
and an approximation factor 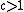 .
.An LSH family
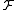 is a family of functions
is a family of functions 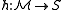 satisfying the following conditions for any two points
satisfying the following conditions for any two points 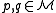 , and a function
, and a function 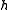 chosen uniformly at random from
chosen uniformly at random from 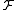 :
:
- if
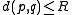 , then
, then 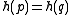 (i.e.,
(i.e.,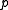 and
and 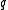 collide) with probability at least
collide) with probability at least 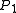 ,
, - if
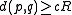 , then
, then 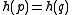 with probability at most
with probability at most 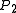 .
.
A family is interesting when
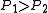 . Such a family
. Such a family 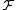 is called
is called  -sensitive.
-sensitive.An alternative definition is defined with respect to a universe of items
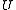 that have a similarity
that have a similaritySimilarity
-Specific definitions:Different fields provide differing definitions of similarity:-In computer science:* string metric, aka string similarity* semantic similarity in computational linguistics-In other fields:...
function
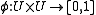 . An LSH scheme is a family of hash function
. An LSH scheme is a family of hash functionHash function
A hash function is any algorithm or subroutine that maps large data sets to smaller data sets, called keys. For example, a single integer can serve as an index to an array...
s
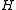 coupled with a probability distribution
coupled with a probability distribution 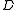 over the functions such that a function
over the functions such that a function  chosen according to
chosen according to 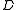 satisfies the property that
satisfies the property that 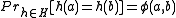 for any
for any 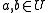 .
.Applications
LSH has been applied to several problem domains including- Near-duplicate detection
- Image similarity identification
- Gene expression similarity identification
- Audio similarity identification
Bit sampling for Hamming distance
One of the easiest ways to construct an LSH family is by bit sampling .This approach works for the Hamming distance
Hamming distance
In information theory, the Hamming distance between two strings of equal length is the number of positions at which the corresponding symbols are different...
over d-dimensional vectors
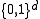 . Here, the family
. Here, the family 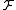 of hash functions is simply the family of all the projections of points on
of hash functions is simply the family of all the projections of points onone of the
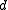 coordinates, i.e.,
coordinates, i.e., 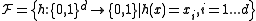 ,
,where
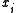 is the
is the 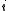 th coordinate of
th coordinate of . A random function
. A random function 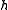 from
from 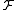 simply selects a random bit from the input point. This family has the following parameters:
simply selects a random bit from the input point. This family has the following parameters: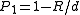 ,
, 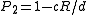 .
.Min-wise independent permutations
Suppose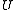 is composed of subsets of some ground set of enumerable items
is composed of subsets of some ground set of enumerable items 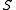 and the similarity function of interest is the Jaccard index
and the similarity function of interest is the Jaccard indexJaccard index
The Jaccard index, also known as the Jaccard similarity coefficient , is a statistic used for comparing the similarity and diversity of sample sets....
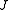 . If
. If  is a permutation on the indices of
is a permutation on the indices of 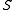 , for
, for  let
let 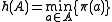 . Each possible choice of
. Each possible choice of  defines a single hash function
defines a single hash function 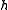 mapping input sets to integers.
mapping input sets to integers.Define the function family
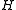 to be the set of all such functions and let
to be the set of all such functions and let 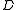 be the uniform distribution. Given two sets
be the uniform distribution. Given two sets 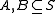 the event that
the event that 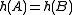 corresponds exactly to the event that the minimizer of
corresponds exactly to the event that the minimizer of  lies inside
lies inside 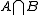 . As
. As 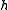 was chosen uniformly at random,
was chosen uniformly at random, 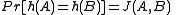 and
and 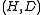 define an LSH scheme for the Jaccard index.
define an LSH scheme for the Jaccard index.Because the symmetric group on n elements has size n!, choosing a truly random permutation from the full symmetric group is infeasible for even moderately sized n. Because of this fact, there has been significant work on finding a family of permutations that is "min-wise independent" - a permutation family for which each element of the domain has equal probability of being the minimum under a randomly chosen
 . It has been established that a min-wise independent family of permutations is at least of size
. It has been established that a min-wise independent family of permutations is at least of size 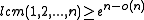 . and that this boundary is tight
. and that this boundary is tightBecause min-wise independent families are too big for practical applications, two variant notions of min-wise independence are introduced: restricted min-wise independent permutations families, and approximate min-wise independent families.
Restricted min-wise independence is the min-wise independence property restricted to certain sets of cardinality at most k .
Approximate min-wise independence differs from the property by at most a fixed
 .
.Random projection
The random projection method of LSH is designed to approximate the cosine distance between vectors. The basic idea of this technique is to choose a random hyperplaneHyperplane
A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...
(defined by a normal unit vector
 ) at the outset and use the hyperplane to hash input vectors.
) at the outset and use the hyperplane to hash input vectors.Given an input vector
 and a hyperplane defined by
and a hyperplane defined by  , we let
, we let 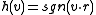 . That is,
. That is, 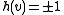 depending on which side of the hyperplane
depending on which side of the hyperplane  lies.
lies.Each possible choice of
 defines a single function. Let
defines a single function. Let  be the set of all such functions and let
be the set of all such functions and let 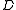 be the uniform distribution once again. It is not difficult to prove that, for two vectors
be the uniform distribution once again. It is not difficult to prove that, for two vectors 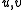 ,
, 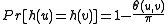 , where
, where 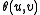 is the angle between
is the angle between  and
and  .
. 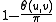 is closely related to
is closely related to 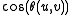 .
.In this instance hashing produces only a single bit. Two vectors' bits match with probability proportional to the cosine of the angle between them.
Stable distributions
The hash function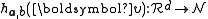 maps a d dimensional vector
maps a d dimensional vector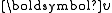 onto a set of integers. Each hash function
onto a set of integers. Each hash functionin the family is indexed by a choice of random
 and
and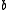 where
where  is a d dimensional
is a d dimensionalvector with
entries chosen independently from a stable distribution and
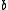 is
isa real number chosen uniformly from the range [0,r]. For a fixed
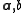 the hash function
the hash function 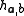 is
isgiven by
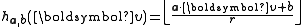 .
.Other construction methods for hash functions have been proposed to better fit the data.
In particular k-means hash functions are better in practice than projection-based hash functions, but without any theoretical guarantee.
LSH algorithm for nearest neighbor search
One of the main application of LSH is to provide efficient nearest neighbor searchNearest neighbor search
Nearest neighbor search , also known as proximity search, similarity search or closest point search, is an optimization problem for finding closest points in metric spaces. The problem is: given a set S of points in a metric space M and a query point q ∈ M, find the closest point in S to q...
algorithms.
Consider any LSH family
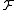 . The
. Thealgorithm has two main parameters: the width parameter
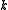 and the
and thenumber of hash tables
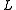 .
.In the first step, we define a new family
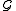 of hash
of hashfunctions
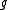 , where each function
, where each function 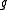 is
isobtained by concatenating
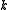 functions
functions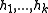 from
from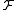 , i.e.,
, i.e., 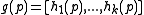 .
.In other words, a random hash function
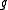 is obtained by
is obtained byconcatenating
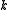 randomly chosen hash functions from
randomly chosen hash functions from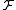 .
.The algorithm then constructs
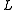 hash tables, each
hash tables, eachcorresponding to
a different randomly chosen hash function
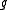 .
.In the preprocessing step we hash all
 points from the data set
points from the data set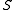 into each of
into each ofthe
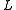 hash tables.
hash tables.Given that the resulting hash tables have only
 non-zero
non-zeroentries,
one can reduce the amount of memory used per each hash table to
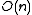 using standard hash functions.
using standard hash functions.Given a query point
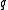 , the algorithm iterates over the
, the algorithm iterates over the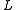 hash functions
hash functions 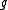 .
.For each
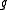 considered, it retrieves the data points that
considered, it retrieves the data points thatare hashed
into the same bucket as
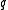 .
.The process is stopped as soon as a point within distance
 from
from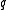 is found.
is found.Given the parameters
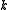 and
and 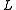 , the algorithm has
, the algorithm hasthe following performance guarantees:
- preprocessing time:
 , where
, where  is the time to evaluate a function
is the time to evaluate a function 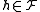 on an input point
on an input point 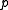 ;
; - space:
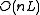 , plus the space for storing data points;
, plus the space for storing data points; - query time:
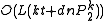 ;
; - the algorithm succeeds in finding a point within distance
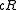 from
from 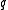 (if it exists) with probability at least
(if it exists) with probability at least 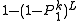 ;
;
For a fixed approximation ratio
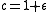 and probabilities
and probabilities and
and 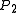 , one can set
, one can set 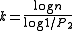 and
and 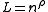 , where
, where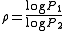 .
.Then one obtains the following performance guarantees:
- preprocessing time:
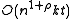 ;
; - space:
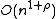 , plus the space for storing data points;
, plus the space for storing data points; - query time:
 ;
;
See also
- Nearest neighbor searchNearest neighbor searchNearest neighbor search , also known as proximity search, similarity search or closest point search, is an optimization problem for finding closest points in metric spaces. The problem is: given a set S of points in a metric space M and a query point q ∈ M, find the closest point in S to q...
- Dimension reduction
- Principal component analysis
- Singular value decompositionSingular value decompositionIn linear algebra, the singular value decomposition is a factorization of a real or complex matrix, with many useful applications in signal processing and statistics....
- Curse of dimensionalityCurse of dimensionalityThe curse of dimensionality refers to various phenomena that arise when analyzing and organizing high-dimensional spaces that do not occur in low-dimensional settings such as the physical space commonly modeled with just three dimensions.There are multiple phenomena referred to by this name in...
- Cluster analysis
- Wavelet compression
- Fourier-related transforms
Further reading
- Samet, H. (2006) Foundations of Multidimensional and Metric Data Structures. Morgan Kaufmann. ISBN 0-12-369446-9
External links
- Alex Andoni's LSH homepage
- LSHKIT: A C++ Locality Sensitive Hashing Library
- Caltech Large Scale Image Search Toolbox: a Matlab toolbox implementing several LSH hash functions, in addition to Kd-Trees, Hierarchical K-Means, and Inverted File search algorithms.

