
Multiplication operator
Encyclopedia
In operator theory
, a multiplication operator is a linear operator T defined on some vector space of functions
and whose value at a function φ is given by multiplication by a fixed function f. That is,
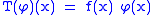
for all φ in the function space and all x in the domain
of φ (which is the same as the domain of f).
This type of operators is often contrasted with composition operator
s. Multiplication operators generalize the notion of operator given by a diagonal matrix
. More precisely, one of the results of operator theory
is a spectral theorem
, which states that every self-adjoint operator
on a Hilbert space
is unitarily equivalent to a multiplication operator on an L2 space
.
X=L2[−1, 3] of complex
-valued square integrable functions on the interval
[−1, 3]. Define the operator: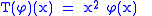
for any function φ in X. This will be a self-adjoint
bounded linear operator with norm
9. Its spectrum will be the interval [0, 9] (the range
of the function x→ x2 defined on [−1, 3]). Indeed, for any complex number λ, the operator T-λ is given by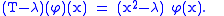
It is invertible if and only if
λ is not in [0, 9], and then its inverse is
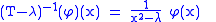
which is another multiplication operator.
This can be easily generalized to characterizing the norm and spectrum of a multiplication operator on any Lp space
.
Operator theory
In mathematics, operator theory is the branch of functional analysis that focuses on bounded linear operators, but which includes closed operators and nonlinear operators.Operator theory also includes the study of algebras of operators....
, a multiplication operator is a linear operator T defined on some vector space of functions
Function space
In mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
and whose value at a function φ is given by multiplication by a fixed function f. That is,
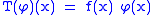
for all φ in the function space and all x in the domain
Domain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
of φ (which is the same as the domain of f).
This type of operators is often contrasted with composition operator
Composition operator
In mathematics, the composition operator C_\phi with symbol \phi is a linear operator defined by the ruleC_\phi = f \circ\phiwhere f \circ\phi denotes function composition. In physics, and especially the area of dynamical systems, the composition operator is usually referred to as the Koopman...
s. Multiplication operators generalize the notion of operator given by a diagonal matrix
Diagonal matrix
In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
. More precisely, one of the results of operator theory
Operator theory
In mathematics, operator theory is the branch of functional analysis that focuses on bounded linear operators, but which includes closed operators and nonlinear operators.Operator theory also includes the study of algebras of operators....
is a spectral theorem
Spectral theorem
In mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized...
, which states that every self-adjoint operator
Self-adjoint operator
In mathematics, on a finite-dimensional inner product space, a self-adjoint operator is an operator that is its own adjoint, or, equivalently, one whose matrix is Hermitian, where a Hermitian matrix is one which is equal to its own conjugate transpose...
on a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
is unitarily equivalent to a multiplication operator on an L2 space
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
.
Example
Consider the Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
X=L2[−1, 3] of complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
-valued square integrable functions on the interval
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
[−1, 3]. Define the operator:
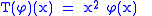
for any function φ in X. This will be a self-adjoint
Self-adjoint operator
In mathematics, on a finite-dimensional inner product space, a self-adjoint operator is an operator that is its own adjoint, or, equivalently, one whose matrix is Hermitian, where a Hermitian matrix is one which is equal to its own conjugate transpose...
bounded linear operator with norm
Operator norm
In mathematics, the operator norm is a means to measure the "size" of certain linear operators. Formally, it is a norm defined on the space of bounded linear operators between two given normed vector spaces.- Introduction and definition :...
9. Its spectrum will be the interval [0, 9] (the range
Range (mathematics)
In mathematics, the range of a function refers to either the codomain or the image of the function, depending upon usage. This ambiguity is illustrated by the function f that maps real numbers to real numbers with f = x^2. Some books say that range of this function is its codomain, the set of all...
of the function x→ x2 defined on [−1, 3]). Indeed, for any complex number λ, the operator T-λ is given by
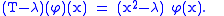
It is invertible if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
λ is not in [0, 9], and then its inverse is
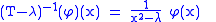
which is another multiplication operator.
This can be easily generalized to characterizing the norm and spectrum of a multiplication operator on any Lp space
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
.
See also
- translation operatorTranslation operatorThe translation operator can refer to these things:* A shift operator, which effects a geometric translation. See also Translation .* An alternative name for the displacement operator in quantum optics....
- shift operatorShift operatorIn mathematics, and in particular functional analysis, the shift operator or translation operator is an operator that takes a function to its translation . In time series analysis, the shift operator is called the lag operator....
- Decomposition of spectrum (functional analysis)Decomposition of spectrum (functional analysis)In mathematics, especially functional analysis, the spectrum of an operator generalizes the notion of eigenvalues. Given an operator, it is sometimes useful to break up the spectrum into various parts...

