
Canonical form
Encyclopedia
Generally, in mathematics
, a canonical form (often called normal form or standard form) of an object is a standard way of presenting that object.
Canonical form can also mean a differential form
that is defined in a natural (canonical) way; see below.
Finding a canonical form is called canonization. In some branches of computer science
the term canonicalization
is adopted.
. A canonical form is given by designating some objects of S to be "in canonical form", such that every object under consideration is equivalent to exactly one object in canonical form. In other words, the canonical forms in S represent the equivalence classes, once and only once. To test whether two objects are equivalent, it then suffices to test their canonical forms for equality.
A canonical form thus provides a classification theorem
and more, in that it not just classifies every class, but gives a distinguished (canonical) representative.
In practical terms, one wants to be able to recognize the canonical forms. There is also a practical, algorithmic question to consider: how to pass from a given object s in S to its canonical form s*? Canonical forms are generally used to make operating with equivalence classes more effective. For example in modular arithmetic
, the canonical form for a residue class is usually taken as the least non-negative integer in it. Operations on classes are carried out by combining these representatives and then reducing the result to its least non-negative residue.
The uniqueness requirement is sometimes relaxed, allowing the forms to be unique up to some finer equivalence relation, like allowing reordering of terms (if there is no natural ordering on terms).
A canonical form may simply be a convention, or a deep theorem.
For example, polynomials are conventionally written with the terms in descending powers: it is more usual to write x2 + x + 30 than x + 30 + x2, although the two forms define the same polynomial. By contrast, the existence of Jordan canonical form for a matrix is a deep theorem.
" some equivalence relation E means that the canonical form is not unique in general, but that if one object has two different canonical forms, they are E-equivalent.
By contrast, there are alternative forms for writing equations. For example, the equation of a line may be written as a linear equation
in point-slope and slope-intercept form.
s include the canonical one-form and canonical symplectic form, important in the study of Hamiltonian mechanics
and symplectic manifold
s.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a canonical form (often called normal form or standard form) of an object is a standard way of presenting that object.
Canonical form can also mean a differential form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
that is defined in a natural (canonical) way; see below.
Finding a canonical form is called canonization. In some branches of computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
the term canonicalization
Canonicalization
In computer science, canonicalization , is a process for converting data that has more than one possible representation into a "standard", "normal", or canonical form...
is adopted.
Definition
Suppose we have some set S of objects, with an equivalence relationEquivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
. A canonical form is given by designating some objects of S to be "in canonical form", such that every object under consideration is equivalent to exactly one object in canonical form. In other words, the canonical forms in S represent the equivalence classes, once and only once. To test whether two objects are equivalent, it then suffices to test their canonical forms for equality.
A canonical form thus provides a classification theorem
Classification theorem
In mathematics, a classification theorem answers the classification problem "What are the objects of a given type, up to some equivalence?". It gives a non-redundant enumeration: each object is equivalent to exactly one class....
and more, in that it not just classifies every class, but gives a distinguished (canonical) representative.
In practical terms, one wants to be able to recognize the canonical forms. There is also a practical, algorithmic question to consider: how to pass from a given object s in S to its canonical form s*? Canonical forms are generally used to make operating with equivalence classes more effective. For example in modular arithmetic
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
, the canonical form for a residue class is usually taken as the least non-negative integer in it. Operations on classes are carried out by combining these representatives and then reducing the result to its least non-negative residue.
The uniqueness requirement is sometimes relaxed, allowing the forms to be unique up to some finer equivalence relation, like allowing reordering of terms (if there is no natural ordering on terms).
A canonical form may simply be a convention, or a deep theorem.
For example, polynomials are conventionally written with the terms in descending powers: it is more usual to write x2 + x + 30 than x + 30 + x2, although the two forms define the same polynomial. By contrast, the existence of Jordan canonical form for a matrix is a deep theorem.
Examples
Note: in this section, "up toUp to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
" some equivalence relation E means that the canonical form is not unique in general, but that if one object has two different canonical forms, they are E-equivalent.
Linear algebra
| Objects | A is equivalent to B if: | Normal form | Notes |
|---|---|---|---|
| Normal Normal matrix A complex square matrix A is a normal matrix ifA^*A=AA^* \ where A* is the conjugate transpose of A. That is, a matrix is normal if it commutes with its conjugate transpose.If A is a real matrix, then A*=AT... matrices over the complex numbers |
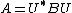 for some unitary matrix U for some unitary matrix U |
Diagonal matrices (up to reordering) | This is the Spectral theorem Spectral theorem In mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized... |
| Matrices over the complex numbers | 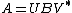 for some unitary matrices U and V for some unitary matrices U and V |
Diagonal matrices with real positive entries (in descending order) | Singular value decomposition Singular value decomposition In linear algebra, the singular value decomposition is a factorization of a real or complex matrix, with many useful applications in signal processing and statistics.... |
| Matrices over an algebraically closed field Algebraically closed field In mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:... |
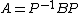 for some invertible matrix P for some invertible matrix P |
Jordan normal form Jordan normal form In linear algebra, a Jordan normal form of a linear operator on a finite-dimensional vector space is an upper triangular matrix of a particular form called Jordan matrix, representing the operator on some basis... (up to reordering of blocks) |
|
| Matrices over a field |  for some invertible matrix P for some invertible matrix P |
Frobenius normal form Frobenius normal form In linear algebra, the Frobenius normal form, Turner binormal projective form or rational canonical form of a square matrix A is a canonical form for matrices that reflects the structure of the minimal polynomial of A and provides a means of detecting whether another matrix B is similar to A... |
|
| Matrices over a principal ideal domain Principal ideal domain In abstract algebra, a principal ideal domain, or PID, is an integral domain in which every ideal is principal, i.e., can be generated by a single element. More generally, a principal ideal ring is a nonzero commutative ring whose ideals are principal, although some authors refer to PIDs as... |
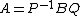 for some invertible Matrices P and Q for some invertible Matrices P and Q |
Smith normal form Smith normal form In mathematics, the Smith normal form is a normal form that can be defined for any matrix with entries in a principal ideal domain . The Smith normal form of a matrix is diagonal, and can be obtained from the original matrix by multiplying on the left and right by invertible square matrices... |
The equivalence is the same as allowing invertible elementary row and column transformations |
| Finite-dimensional vector spaces over a field K | A and B are isomorphic as vector spaces | 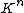 , n a non-negative integer , n a non-negative integer |
Classical logic
- Negation normal form
- Conjunctive normal formConjunctive normal formIn Boolean logic, a formula is in conjunctive normal form if it is a conjunction of clauses, where a clause is a disjunction of literals.As a normal form, it is useful in automated theorem proving...
- Disjunctive normal formDisjunctive normal formIn boolean logic, a disjunctive normal form is a standardization of a logical formula which is a disjunction of conjunctive clauses. As a normal form, it is useful in automated theorem proving. A logical formula is considered to be in DNF if and only if it is a disjunction of one or more...
- Algebraic normal formAlgebraic normal formIn Boolean logic, the algebraic normal form is a method of standardizing and normalizing logical formulas. As a normal form, it can be used in automated theorem proving , but is more commonly used in the design of cryptographic random number generators, specifically linear feedback shift registers...
- Canonical form (Boolean algebra)Canonical form (Boolean algebra)In Boolean algebra, any Boolean function can be expressed in a canonical form using the dual concepts of minterms and maxterms. Minterms are called products because they are the logical AND of a set of variables, and maxterms are called sums because they are the logical OR of a set of variables In...
- Prenex normal formPrenex normal formA formula of the predicate calculus is in prenex normal form if it is written as a string of quantifiers followed by a quantifier-free part .Every formula in classical logic is equivalent to a formula in prenex normal form...
- Skolem normal formSkolem normal formReduction to Skolem normal form is a method for removing existential quantifiers from formal logic statements, often performed as the first step in an automated theorem prover....
Functional analysis
| Objects | A is equivalent to B if: | Normal form |
|---|---|---|
| Hilbert spaces | A and B are isometrically isomorphic as Hilbert spaces | 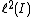 sequence spaces (up to exchanging the index set I with another index set of the same cardinality) sequence spaces (up to exchanging the index set I with another index set of the same cardinality) |
Commutative 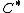 -algebras with unit -algebras with unit |
A and B are isomorphic as 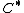 -algebras -algebras |
The algebra  of continuous functions on a compact of continuous functions on a compactCompact space In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces... Hausdorff space Hausdorff space In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently... , up to homeomorphism Homeomorphism In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are... of the base space. |
Algebra
| Objects | A is equivalent to B if: | Normal form |
|---|---|---|
| Finitely generated R-modules with R a principal ideal domain Principal ideal domain In abstract algebra, a principal ideal domain, or PID, is an integral domain in which every ideal is principal, i.e., can be generated by a single element. More generally, a principal ideal ring is a nonzero commutative ring whose ideals are principal, although some authors refer to PIDs as... |
A and B are isomorphic as R-modules | Primary decomposition (up to reordering) or invariant factor decomposition Structure theorem for finitely generated modules over a principal ideal domain In mathematics, in the field of abstract algebra, the structure theorem for finitely generated modules over a principal ideal domain is a generalization of the fundamental theorem of finitely generated abelian groups and roughly states that finitely generated modules can be uniquely decomposed in... |
Geometry
- The equation of a line: Ax + By = C
- C = 0 or C = 1
- The equation of a circle:
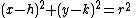
By contrast, there are alternative forms for writing equations. For example, the equation of a line may be written as a linear equation
Linear equation
A linear equation is an algebraic equation in which each term is either a constant or the product of a constant and a single variable....
in point-slope and slope-intercept form.
Mathematical notation
Standard form is used by many mathematicians and scientists to write extremely large numbers in a more concise and understandable way.Set theory
- Cantor normal form of an ordinal numberOrdinal numberIn set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
Lambda calculus
- Beta normal form if no beta reduction is possible; Lambda calculus is a particular case of an abstract rewriting system.
Differential forms
Canonical differential formDifferential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
s include the canonical one-form and canonical symplectic form, important in the study of Hamiltonian mechanics
Hamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
and symplectic manifold
Symplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
s.

