
Orthogonal Procrustes problem
Encyclopedia
The orthogonal Procrustes problem is a matrix approximation problem in linear algebra
. In its classical form, one is given two matrices
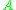 and
and 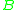 and asked to find an orthogonal matrix
and asked to find an orthogonal matrix
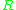 which most closely maps
which most closely maps 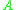 to
to 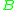 . Specifically,
. Specifically,
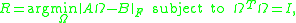
where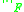 denotes the Frobenius norm.
denotes the Frobenius norm.
The name Procrustes
refers to a bandit from Greek mythology who made his victims fit his bed either by stretching their limbs or cutting them off.
in a 1964 thesis. The individual solution was later published.
This problem is equivalent to finding the nearest orthogonal matrix to a given matrix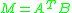 . To find this orthogonal matrix
. To find this orthogonal matrix 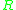 , one uses the singular value decomposition
, one uses the singular value decomposition
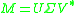
to write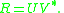
Alternately, one might constrain it by only allowing rotation matrices (i.e. orthogonal matrices with determinant
1, also known as special orthogonal matrices
). In this case, one can write (using the above decomposition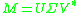 )
)
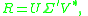
where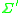 is a modified
is a modified 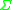 , with the smallest singular value replaced by
, with the smallest singular value replaced by 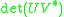 (+1 or -1), and the other singular values replaced by 1, so that the determinant of R is guaranteed to be positive.
(+1 or -1), and the other singular values replaced by 1, so that the determinant of R is guaranteed to be positive.
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
. In its classical form, one is given two matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
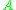 and
and 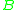 and asked to find an orthogonal matrix
and asked to find an orthogonal matrixOrthogonal matrix
In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
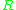 which most closely maps
which most closely maps 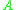 to
to 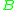 . Specifically,
. Specifically,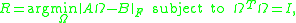
where
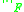 denotes the Frobenius norm.
denotes the Frobenius norm.The name Procrustes
Procrustes
In Greek mythology Procrustes or "the stretcher [who hammers out the metal]", also known as Prokoptas or Damastes "subduer", was a rogue smith and bandit from Attica who physically attacked people by stretching them or cutting off their legs, so as to force them to fit the size of an iron bed...
refers to a bandit from Greek mythology who made his victims fit his bed either by stretching their limbs or cutting them off.
Solution
This problem was originally solved by Peter SchonemannPeter Schonemann
Peter H. Schönemann was a German born psychometrician and statistical expert. He was Professor Emeritus in the Department of Psychological Sciences at Purdue University. His research interests included multivariate statistics, multidimensional scaling and measurement, quantitative behavior...
in a 1964 thesis. The individual solution was later published.
This problem is equivalent to finding the nearest orthogonal matrix to a given matrix
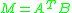 . To find this orthogonal matrix
. To find this orthogonal matrix 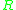 , one uses the singular value decomposition
, one uses the singular value decompositionSingular value decomposition
In linear algebra, the singular value decomposition is a factorization of a real or complex matrix, with many useful applications in signal processing and statistics....
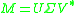
to write
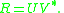
Generalized/constrained Procrustes problems
There are a number of related problems to the classical orthogonal Procrustes problem. One might generalize it by seeking the closest matrix in which the columns are orthogonal, but not necessarily orthonormal.Alternately, one might constrain it by only allowing rotation matrices (i.e. orthogonal matrices with determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
1, also known as special orthogonal matrices
Orthogonal matrix
In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
). In this case, one can write (using the above decomposition
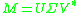 )
)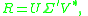
where
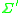 is a modified
is a modified 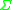 , with the smallest singular value replaced by
, with the smallest singular value replaced by 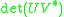 (+1 or -1), and the other singular values replaced by 1, so that the determinant of R is guaranteed to be positive.
(+1 or -1), and the other singular values replaced by 1, so that the determinant of R is guaranteed to be positive.

