Unsolved problems in mathematics - AbsoluteAstronomy.com

This article lists some unsolved problems in mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

. See individual articles for details and sources.

Millennium Prize Problems

Of the seven Millennium Prize Problems

Millennium Prize Problems

The Millennium Prize Problems are seven problems in mathematics that were stated by the Clay Mathematics Institute in 2000. As of September 2011, six of the problems remain unsolved. A correct solution to any of the problems results in a US$1,000,000 prize being awarded by the institute...

set by the Clay Mathematics Institute

Clay Mathematics Institute

The Clay Mathematics Institute is a private, non-profit foundation, based in Cambridge, Massachusetts. The Institute is dedicated to increasing and disseminating mathematical knowledge. It gives out various awards and sponsorships to promising mathematicians. The institute was founded in 1998...

, six have yet to be solved:

P versus NP
Hodge conjecture
Hodge conjecture
The Hodge conjecture is a major unsolved problem in algebraic geometry which relates the algebraic topology of a non-singular complex algebraic variety and the subvarieties of that variety. More specifically, the conjecture says that certain de Rham cohomology classes are algebraic, that is, they...
Riemann hypothesis
Riemann hypothesis
In mathematics, the Riemann hypothesis, proposed by , is a conjecture about the location of the zeros of the Riemann zeta function which states that all non-trivial zeros have real part 1/2...
Yang–Mills existence and mass gap
Yang–Mills existence and mass gap
In mathematics, the Yang-Mills existence and mass gap problem is an unsolved problem and one of the seven Millennium Prize Problems defined by the Clay Mathematics Institute which has offered a prize of US$1,000,000 to a person solving it....
Navier–Stokes existence and smoothness
Birch and Swinnerton-Dyer conjecture
Birch and Swinnerton-Dyer conjecture
In mathematics, the Birch and Swinnerton-Dyer conjecture is an open problem in the field of number theory. Its status as one of the most challenging mathematical questions has become widely recognized; the conjecture was chosen as one of the seven Millennium Prize Problems listed by the Clay...

.

The seventh problem, the Poincaré conjecture

Poincaré conjecture

In mathematics, the Poincaré conjecture is a theorem about the characterization of the three-dimensional sphere , which is the hypersphere that bounds the unit ball in four-dimensional space...

, has been solved. The smooth four-dimensional Poincaré conjecture is still unsolved. That is, can a four-dimensional topological sphere have two or more inequivalent smooth structure

Smooth structure

In mathematics, a smooth structure on a manifold allows for an unambiguous notion of smooth function. In particular, a smooth structure allows one to perform mathematical analysis on the manifold....

Additive number theory

Goldbach's conjecture
Goldbach's conjecture
Goldbach's conjecture is one of the oldest unsolved problems in number theory and in all of mathematics. It states:A Goldbach number is a number that can be expressed as the sum of two odd primes...

and its weak version
Goldbach's weak conjecture
In number theory, Goldbach's weak conjecture, also known as the odd Goldbach conjecture, the ternary Goldbach problem, or the 3-primes problem, states that:...
The values of g(k) and G(k) in Waring's problem
Waring's problem
In number theory, Waring's problem, proposed in 1770 by Edward Waring, asks whether for every natural number k there exists an associated positive integer s such that every natural number is the sum of at most s kth powers of natural numbers...
Collatz conjecture
Collatz conjecture
The Collatz conjecture is a conjecture in mathematics named after Lothar Collatz, who first proposed it in 1937. The conjecture is also known as the 3n + 1 conjecture, the Ulam conjecture , Kakutani's problem , the Thwaites conjecture , Hasse's algorithm The Collatz conjecture is a...

(3n + 1 conjecture)
Gilbreath's conjecture
Gilbreath's conjecture
Gilbreath's conjecture is a hypothesis, or a conjecture, in number theory regarding the sequences generated by applying the forward difference operator to consecutive prime numbers and leaving the results unsigned, and then repeating this process on consecutive terms in the resulting sequence, and...
Erdős conjecture on arithmetic progressions
Erdős–Turán conjecture on additive bases
Erdős–Turán conjecture on additive bases
The Erdős–Turán conjecture is an old unsolved problem in additive number theory posed by Paul Erdős and Pál Turán in 1941.-History:...
Pollock octahedral numbers conjecture
Pollock octahedral numbers conjecture
In additive number theory, the Pollock octahedral numbers conjecture is an unproven conjecture that every positive integer is the sum of at most seven octahedral numbers. It was first stated in 1850 by Sir Frederick Pollock, better known as a lawyer and politician but also a contributor of papers...

Number theory: prime numbers

Catalan's Mersenne conjecture
Twin prime conjecture
Twin prime
A twin prime is a prime number that differs from another prime number by two. Except for the pair , this is the smallest possible difference between two primes. Some examples of twin prime pairs are , , , , and...
Are there infinitely many prime quadruplets?
Are there infinitely many Mersenne prime
Mersenne prime
In mathematics, a Mersenne number, named after Marin Mersenne , is a positive integer that is one less than a power of two: M_p=2^p-1.\,...

s (Lenstra–Pomerance–Wagstaff conjecture); equivalently, infinitely many even perfect number
Perfect number
In number theory, a perfect number is a positive integer that is equal to the sum of its proper positive divisors, that is, the sum of its positive divisors excluding the number itself . Equivalently, a perfect number is a number that is half the sum of all of its positive divisors i.e...

s?
Are there infinitely many Sophie Germain prime
Sophie Germain prime
In number theory, a prime number p is a Sophie Germain prime if 2p + 1 is also prime. For example, 23 is a Sophie Germain prime because it is a prime and 2 × 23 + 1 = 47, and 47 is also a prime number...

s?
Are there infinitely many regular primes, and if so is their relative density ?
Are there infinitely many Cullen primes?
Are there infinitely many palindromic prime
Palindromic prime
A palindromic prime is a prime number that is also a palindromic number. Palindromicity depends on the base of the numbering system and its writing conventions, while primality is independent of such concerns...

s in base 10?
Are there infinitely many Fibonacci prime
Fibonacci prime
A Fibonacci prime is a Fibonacci number that is prime, a type of integer sequence prime.The first Fibonacci primes are :-Known Fibonacci primes:It is not known if there are infinitely many Fibonacci primes...

s?
Are there infinitely many Wilson prime
Wilson prime
A Wilson prime, named after English mathematician John Wilson, is a prime number p such that p2 divides ! + 1, where "!" denotes the factorial function; compare this with Wilson's theorem, which states that every prime p divides ! + 1.The only known Wilson primes are 5, 13, and...

s?
Are there any Wall–Sun–Sun primes?
Is every Fermat number 2^2ⁿ + 1 composite for ?
Is 78,557 the lowest Sierpinski number?
Is 509,203 the lowest Riesel number
Riesel number
In mathematics, a Riesel number is an odd natural number k for which the integers of the form k·2n − 1 are composite for all natural numbers n....

?
Fortune's conjecture (that no Fortunate number is composite)
Polignac's conjecture
Polignac's conjecture
In number theory, Polignac's conjecture was made by Alphonse de Polignac in 1849 and states:The conjecture has not been proven or disproven for any value of n....
Landau's problems
Landau's problems
At the 1912 International Congress of Mathematicians, Edmund Landau listed four basic problems about primes. These problems were characterised in his speech as "unattackable at the present state of science" and are now known as Landau's problems...
Does every prime number appear in the Euclid–Mullin sequence?

General number theory

abc conjecture
Abc conjecture
The abc conjecture is a conjecture in number theory, first proposed by Joseph Oesterlé and David Masser in 1985. The conjecture is stated in terms of three positive integers, a, b and c , which have no common factor and satisfy a + b = c...
Do any odd perfect numbers exist?
Do quasiperfect number
Quasiperfect number
In mathematics, a quasiperfect number is a theoretical natural number n for which the sum of all its divisors is equal to 2n + 1...

s exist?
Do any odd weird number
Weird number
In number theory, a weird number is a natural number that is abundant but not semiperfect.In other words, the sum of the proper divisors of the number is greater than the number, but no subset of those divisors sums to the number itself.- Examples :The smallest weird number is 70...

s exist?
Do any Lychrel number
Lychrel number
A Lychrel number is a natural number which cannot form a palindrome through the iterative process of repeatedly reversing its base 10 digits and adding the resulting numbers. This process is called the 196-algorithm. The name "Lychrel" was coined by Wade VanLandingham—a rough anagram of his...

s exist?
Is 10 a solitary number?
Do any Taxicab(5, 2, n)
Generalized taxicab number
In mathematics, the generalized taxicab number Taxicab is the smallest number which can be expressed as the sum of j kth positive powers in n different ways...

exist for n>1?
Brocard's problem
Brocard's problem
Brocard's problem asks to find integer values of n for whichn!+1 = m^2,where n! is the factorial. It was posed by Henri Brocard in a pair of articles in 1876 and 1885, and independently in 1913 by Ramanujan.-Brown numbers:...

: existence of integers, n,m, such that n!+1=m² other than n=4,5,7
Distribution and upper bound of mimic numbers
Littlewood conjecture

Algebraic number theory

Are there infinitely many real quadratic number fields with unique factorization?

Discrete geometry

Solving the Happy Ending problem
Happy Ending problem
The Happy Ending problem is the following statement:This was one of the original results that led to the development of Ramsey theory....

for arbitrary
Finding matching upper and lower bounds for K-sets
K-set (geometry)
In discrete geometry, a k-set of a finite point set S in the Euclidean plane is a subset of k elements of S that can be strictly separated from the remaining points by a line. More generally, in Euclidean space of higher dimensions, a k-set of a finite point set is a subset of k elements that can...

and halving lines
The Hadwiger conjecture
Hadwiger conjecture (combinatorial geometry)
In combinatorial geometry, the Hadwiger conjecture states that any convex body in n-dimensional Euclidean space can be covered by 2n or fewer smaller bodies homothetic with the original body, and that furthermore, the upper bound of 2n is necessary iff the body is a parallelpiped...

on covering n-dimensional convex bodies with at most 2ⁿ smaller copies

Ramsey theory

The values of the Ramsey numbers, particularly
The values of the Van der Waerden numbers

General algebra

Hilbert's sixteenth problem
Hilbert's sixteenth problem
Hilbert's 16th problem was posed by David Hilbert at the Paris conference of the International Congress of Mathematicians in 1900, together with the other 22 problems....
Hadamard conjecture
Existence of perfect cuboids
Euler brick
In mathematics, an Euler brick, named after Leonhard Euler, is a cuboid whose edges and face diagonals all have integer lengths. A primitive Euler brick is an Euler brick whose edge lengths are relatively prime.- Properties :...

Combinatorics

Number of Magic square
Magic square
In recreational mathematics, a magic square of order n is an arrangement of n2 numbers, usually distinct integers, in a square, such that the n numbers in all rows, all columns, and both diagonals sum to the same constant. A normal magic square contains the integers from 1 to n2...

s
Finding a formula for the probability that two elements chosen at random generate the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
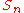
Frankl's union-closed sets conjecture
Union-closed sets conjecture
In combinatorial mathematics, the union-closed sets conjecture is an elementary problem, posed by Péter Frankl in 1979 and still open. A family of sets is said to be union-closed if the union of any two sets from the family remains in the family...

: for any family of sets closed under sums there exists an element (of the underlying space) belonging to half or more of the sets
The Lonely runner conjecture
Lonely runner conjecture
In number theory, and especially the study of diophantine approximation, the lonely runner conjecture is a conjecture originally due to J. M. Wills in 1967. Applications of the conjecture are widespread in mathematics; they include view obstruction problems and calculating the chromatic number of...

: if runners with pairwise distinct speeds run round a track of unit length, will every runner be "lonely" (that is, be more than a distance 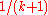from each other runner) at some time?
Singmaster's conjecture: is there a finite upper bound on the multiplicities of the entries greater than 1 in Pascal's triangle?
The 1/3–2/3 conjecture
1/3–2/3 conjecture
In order theory, a branch of mathematics, the 1/3–2/3 conjecture states that, if one is comparison sorting a set of items then, no matter what comparisons may have already been performed, it is always possible to choose the next comparison in such a way that it will reduce the number of possible...

: does every finite partially ordered set
Partially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...

contain two elements x and y such that the probability that x appears before y in a random linear extension
Linear extension
In order theory, a branch of mathematics, a linear extension of a partial order is a linear order that is compatible with the partial order.-Definitions:...

is between 1/3 and 2/3?
Conway's thrackle conjecture
Conway's thrackle conjecture
A thrackle is an embedding of a graph, such that each edge is a Jordan arcand every pair of edges meet once. Edges may either meet at a common endpoint, or, if they have no endpoints in common, at a point in their interiors. In the latter case, the crossing must be transverse.John H...

Graph theory

Barnette's conjecture
Barnette's conjecture
Barnette's conjecture is an unsolved problem in graph theory, a branch of mathematics, concerning Hamiltonian cycles in graphs. It is named after David W...

that every cubic bipartite three-connected planar graph has a Hamiltonian cycle
The Erdős–Gyárfás conjecture
Erdos–Gyárfás conjecture
In graph theory, the unproven Erdős–Gyárfás conjecture, made in 1995 by the prolific mathematician Paul Erdős and his collaborator András Gyárfás, states that any graph with minimum degree 3 contains a simple cycle whose length is a power of two...

on cycles with power-of-two lengths in cubic graphs
The Hadwiger conjecture
Hadwiger conjecture (graph theory)
In graph theory, the Hadwiger conjecture states that, if all proper colorings of an undirected graph G use k or more colors, then one can find k disjoint connected subgraphs of G such that each subgraph is connected by an edge to each other subgraph...

relating coloring to clique minors
The Erdős–Faber–Lovász conjecture
Erdos–Faber–Lovász conjecture
In graph theory, the Erdős–Faber–Lovász conjecture is an unsolved problem about graph coloring, named after Paul Erdős, Vance Faber, and László Lovász, who formulated it in 1972...

on coloring unions of cliques
The total coloring conjecture
The list coloring conjecture
The Ringel–Kotzig conjecture
Graceful labeling
In graph theory, a graceful labeling of a graph with e edges is a labeling of its vertices with distinct integers between 0 and e inclusive, such that each edge is uniquely identified by the positive, or absolute difference between its endpoints. A graph which admits a graceful labeling is called a...

on graceful labeling of trees
The Hadwiger–Nelson problem
Hadwiger–Nelson problem
In geometric graph theory, the Hadwiger–Nelson problem, named after Hugo Hadwiger and Edward Nelson, asks for the minimum number of colors required to color the plane such that no two points at distance one from each other have the same color. The answer is unknown, but has been narrowed down to...

on the chromatic number of unit distance graphs
Deriving a closed-form expression for the percolation threshold
Percolation threshold
Percolation threshold is a mathematical term related to percolation theory, which is the formation of long-range connectivity in random systems. Below the threshold a giant connected component does not exist while above it, there exists a giant component of the order of system size...

values, especially (square site)
Tutte's conjectures that every bridgeless graph has a nowhere-zero 5-flow
Nowhere-zero flows
In graph theory, nowhere-zero flows are a special type of network flow which is related to coloring planar graphs. Let G = be a directed graph and let M be an abelian group...

and every bridgeless graph without the Petersen graph
Petersen graph
In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named for Julius Petersen, who in 1898 constructed it...

as a minor
Minor (graph theory)
In graph theory, an undirected graph H is called a minor of the graph G if H is isomorphic to a graph that can be obtained by zero or more edge contractions on a subgraph of G....

has a nowhere-zero 4-flow
The Reconstruction conjecture
Reconstruction conjecture
Informally, the reconstruction conjecture in graph theory says that graphs are determined uniquely by their subgraphs. It is due to Kelly and Ulam.-Formal statements:...

and New digraph reconstruction conjecture concerning whether or not a graph is recognizable by the vertex deleted subgraphs.
The cycle double cover conjecture that every bridgeless graph has a family of cycles that includes each edge twice.
Does a Moore graph with girth 5 and degree 57 exist?

Analysis
Analysis
Analysis is the process of breaking a complex topic or substance into smaller parts to gain a better understanding of it. The technique has been applied in the study of mathematics and logic since before Aristotle , though analysis as a formal concept is a relatively recent development.The word is...

the Jacobian conjecture
Jacobian conjecture
In mathematics, the Jacobian conjecture is a celebrated problem on polynomials in several variables. It was first posed in 1939 by Ott-Heinrich Keller...
Schanuel's conjecture
Schanuel's conjecture
In mathematics, specifically transcendence theory, Schanuel's conjecture is a conjecture made by Stephen Schanuel in the 1960s concerning the transcendence degree of certain field extensions of the rational numbers.-Statement:The conjecture is as follows:...
Lehmer's conjecture
Lehmer's conjecture
Lehmer's conjecture, also known as the Lehmer's Mahler measure problem, is a problem in number theory. Derrick Henry Lehmer conjectured that the Mahler measure of any integral polynomial...
Pompeiu problem
Pompeiu problem
In mathematics, the Pompeiu problem is a conjecture in integral geometry, named for Dimitrie Pompeiu, who posed the problem in 1929,as follows. Suppose f is a nonzero continuous function defined on a Euclidean space, and K is a simply connected Lipschitz domain, so that the integral of f vanishes...
Is 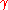(the Euler–Mascheroni constant
Euler–Mascheroni constant
The Euler–Mascheroni constant is a mathematical constant recurring in analysis and number theory, usually denoted by the lowercase Greek letter ....

) irrational?
the Khabibullin’s conjecture on integral inequalities
Khabibullin’s conjecture on integral inequalities
In mathematics, Khabibullin's conjecture, named after B. N. Khabibullin, is related to Paley's problem for plurisubharmonic functions and to various extremal problems in the theory of entire functions of several variables....

Dynamics

Fürstenberg conjecture – Is every invariant and ergodic
Ergodicity
In mathematics, the term ergodic is used to describe a dynamical system which, broadly speaking, has the same behavior averaged over time as averaged over space. In physics the term is used to imply that a system satisfies the ergodic hypothesis of thermodynamics.-Etymology:The word ergodic is...

measure for the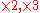 action on the circle either Lebesgue or atomic?
Margulis
Grigory Margulis
Gregori Aleksandrovich Margulis is a Russian mathematician known for his far-reaching work on lattices in Lie groups, and the introduction of methods from ergodic theory into diophantine approximation. He was awarded a Fields Medal in 1978 and a Wolf Prize in Mathematics in 2005, becoming the...

conjecture — Measure classification for diagonalizable actions in higher-rank groups

Partial differential equations

Regularity of solutions of Vlasov–Maxwell equations
Regularity of solutions of Euler equations
Euler equations
In fluid dynamics, the Euler equations are a set of equations governing inviscid flow. They are named after Leonhard Euler. The equations represent conservation of mass , momentum, and energy, corresponding to the Navier–Stokes equations with zero viscosity and heat conduction terms. Historically,...

Group theory

Is every finitely presented periodic group
Periodic group
In group theory, a periodic group or a torsion group is a group in which each element has finite order. All finite groups are periodic. The concept of a periodic group should not be confused with that of a cyclic group, although all finite cyclic groups are periodic.The exponent of a periodic group...

finite?
The inverse Galois problem
Inverse Galois problem
In Galois theory, the inverse Galois problem concerns whether or not every finite group appears as the Galois group of some Galois extension of the rational numbers Q. This problem, first posed in the 19th century, is unsolved....
For which positive integers m, n is the free Burnside group finite? In particular, is finite?

Set theory

The problem of finding the ultimate core model
Core model
In set theory, the core model is a definable inner model of the universe of all sets. Even though set theorists refer to "the core model", it is not a uniquely identified mathematical object. Rather, it is a class of inner models that under the right set theoretic assumptions have very special...

, one that contains all large cardinals
Large cardinal property
In the mathematical field of set theory, a large cardinal property is a certain kind of property of transfinite cardinal numbers. Cardinals with such properties are, as the name suggests, generally very "large"...

.
If ℵ_ω is a strong limit cardinal, then 2^ℵ_ω < ℵ_ω₁ (see Singular cardinals hypothesis). The best bound, ℵ_ω₄, was obtained by Shelah
Saharon Shelah
Saharon Shelah is an Israeli mathematician. He is a professor of mathematics at the Hebrew University of Jerusalem and Rutgers University in New Jersey.-Biography:...

using his pcf theory
PCF theory
PCF theory is the name of a mathematical theory, introduced by Saharon , that deals with the cofinality of the ultraproducts of ordered sets. It gives strong upper bounds on the cardinalities of power sets of singular cardinals, and has many more applications as well...

.
Woodin's
W. Hugh Woodin
William Hugh Woodin is an American mathematician and set theorist at University of California, Berkeley. He has made many notable contributions to the theory of inner models and determinacy. A type of large cardinal, the Woodin cardinal, bears his name.-Biography:Born in Tucson, Arizona, Woodin...

Ω-hypothesis.
Does the consistency
Consistency
Consistency can refer to:* Consistency , the psychological need to be consistent with prior acts and statements* "Consistency", an 1887 speech by Mark Twain...

of the existence of a strongly compact cardinal
Strongly compact cardinal
In mathematical set theory, a strongly compact cardinal is a certain kind of large cardinal number; their existence can neither be proven nor disproven from the standard axioms of set theory....

imply the consistent existence of a supercompact cardinal?
(Woodin
W. Hugh Woodin
William Hugh Woodin is an American mathematician and set theorist at University of California, Berkeley. He has made many notable contributions to the theory of inner models and determinacy. A type of large cardinal, the Woodin cardinal, bears his name.-Biography:Born in Tucson, Arizona, Woodin...

) Does the Generalized Continuum Hypothesis below a strongly compact cardinal
Strongly compact cardinal
In mathematical set theory, a strongly compact cardinal is a certain kind of large cardinal number; their existence can neither be proven nor disproven from the standard axioms of set theory....

imply the Generalized Continuum Hypothesis everywhere?
Does there exist a Jonsson algebra
Jónsson cardinal
In set theory, a Jónsson cardinal is a certain kind of large cardinal number.An uncountable cardinal number κ is said to be Jónsson if for every function f: [κ]...

on ℵ_ω?
Without assuming the axiom of choice, can a nontrivial elementary embedding
Reinhardt cardinal
In set theory, a branch of mathematics, a Reinhardt cardinal is a large cardinal κ, suggested by , that is the critical point of a non-trivial elementary embedding j of V into itself....

V→V exist?
Is it consistent that ?
Does the Generalized Continuum Hypothesis entail
Diamondsuit
In mathematics, and particularly in axiomatic set theory, the diamond principle ◊ is a combinatorial principle introduced by that holds in the constructible universe and that implies the continuum hypothesis...

for every singular cardinal ?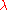

Other

Invariant subspace problem
Problems in Latin squares
Problems in Latin squares
In mathematics, the theory of Latin squares is an active research area with many open problems. As in other areas of mathematics, such problems are often made public at professional conferences and meetings...
Problems in loop theory and quasigroup theory
Problems in loop theory and quasigroup theory
In mathematics, especially abstract algebra, loop theory and quasigroup theory are active research areas with many open problems. As in other areas of mathematics, such problems are often made public at professional conferences and meetings...
Dixmier conjecture
Dixmier conjecture
In algebra the Dixmier conjecture, asked by , is the conjecture that any endomorphism of a Weyl algebra is an automorphism. showed that the Dixmier conjecture is equivalent to the Jacobian conjecture....

Problems solved recently

Circular law
Circular law
In probability theory, more specifically the study of random matrices, the circular law describes the distribution of eigenvalues of an n \times n random matrix with independent and identically distributed entries in the limit n \to \infty ....

(Terence Tao
Terence Tao
Terence Chi-Shen Tao FRS is an Australian mathematician working primarily on harmonic analysis, partial differential equations, combinatorics, analytic number theory and representation theory...

and Van H. Vu
Van H. Vu
Van H. Vu is a Vietnamese mathematician, a professor of mathematics at Yale University and the 2008 winner of the Pólya Prize of the Society for Industrial and Applied Mathematics for his work on concentration of measure. He is a collaborator of Terence Tao....

, 2010)
Hirsch conjecture
Hirsch conjecture
In mathematical programming and polyhedral combinatorics, Hirsch's conjecture states that the edge-vertex graph of an n-facet polytope in d-dimensional Euclidean space has diameter no more than n − d. That is, any two vertices of the polytope must be connected to each other by a...

(as announced by Francisco Santos Leal, 2010)
Road coloring conjecture
Road coloring conjecture
In graph theory the road coloring theorem, known until recently as the road coloring conjecture, deals with synchronized instructions. The issue involves whether by using such instructions, one can reach or locate an object or destination from any other point within a network...

(Avraham Trahtman
Avraham Trahtman
Avraham Trahtman is a mathematician at Bar-Ilan University . In 2007, Trahtman solved a problem in combinatorics that had been open for 37 years, the Road Coloring Conjecture posed in 1970.-Road coloring problem posed and solved:...

, 2007)
The Angel problem
Angel problem
The angel problem is a question in game theory proposed by John Horton Conway. The game is commonly referred to as the Angels and Devils game. The game is played by two players called the angel and the devil. It is played on an infinite chessboard...

(Various independent proofs, 2006)
The Langlands–Shelstad fundamental lemma (Ngô Bảo Châu
Ngo Bao Chau
Ngô Bảo Châu is a Vietnamese and French mathematician at the University of Chicago, best known for proving the fundamental lemma for automorphic forms proposed by Robert Langlands and Diana Shelstad. He is the first Vietnamese to receive the Fields Medal.- Biography :Chau was born in 1972, the...

and Gérard Laumon
Gérard Laumon
Gérard Laumon is a French mathematician. He studied at the École Normale Supérieure and Paris-Sud 11 University, Orsay.In 2004 Laumon and Ngô Bảo Châu received the Clay Research Award for the proof of the Langlands and Shelstad's Fundamental Lemma for unitary groups, a key component in the...

, 2004)
Stanley–Wilf conjecture (Gábor Tardos
Gábor Tardos
Gábor Tardos is a Hungarian mathematician, currently a professor and Canada Research Chair at Simon Fraser University. He works mainly in combinatorics and computer science...

and Adam Marcus, 2004)
Green–Tao theorem (Ben J. Green and Terence Tao
Terence Tao
Terence Chi-Shen Tao FRS is an Australian mathematician working primarily on harmonic analysis, partial differential equations, combinatorics, analytic number theory and representation theory...

, 2004)
Cameron–Erdős conjecture (Ben J. Green, 2003, conjectured by Paul)
Poincaré conjecture
Poincaré conjecture
In mathematics, the Poincaré conjecture is a theorem about the characterization of the three-dimensional sphere , which is the hypersphere that bounds the unit ball in four-dimensional space...

(Grigori Perelman
Grigori Perelman
Grigori Yakovlevich Perelman is a Russian mathematician who has made landmark contributions to Riemannian geometry and geometric topology.In 1992, Perelman proved the soul conjecture. In 2002, he proved Thurston's geometrization conjecture...

, 2002)
Catalan's conjecture
Mihailescu's theorem
Catalan's conjecture is a theorem in number theory that was conjectured by the mathematician Eugène Charles Catalan in 1844 and proven in 2002 by Preda Mihăilescu....

(Preda Mihăilescu
Preda Mihailescu
Preda V. Mihăilescu is a Romanian mathematician, best known for his proof of Catalan's conjecture.Born in Bucharest, he is the brother of Vintilă Mihăilescu. After leaving Romania in 1973, he settled in Switzerland. He studied mathematics and computer science in Zürich, receiving his Ph.D. from...

, 2002)
Kato's conjecture
Kato's conjecture
Kato's conjecture is a mathematical problem named after mathematician Tosio Kato, of the University of California, Berkeley. Kato initially posed the problem in 1953....

(Auscher, Hofmann, Lacey, McIntosh, and Tchamitchian, 2001)
The Langlands correspondence for function fields (Laurent Lafforgue
Laurent Lafforgue
Laurent Lafforgue is a French mathematician.He won 2 silver medals at International Mathematical Olympiad in 1984 and 1985....

, 1999)
Taniyama-Shimura conjecture (Wiles, Breuil, Conrad, Diamond, and Taylor, 1999)
Kepler conjecture
Kepler conjecture
The Kepler conjecture, named after the 17th-century German astronomer Johannes Kepler, is a mathematical conjecture about sphere packing in three-dimensional Euclidean space. It says that no arrangement of equally sized spheres filling space has a greater average density than that of the cubic...

(Thomas Hales
Thomas Callister Hales
Thomas Callister Hales is an American mathematician. He is known for his 1998 computer-aided proof of the Kepler conjecture, a centuries-old problem in discrete geometry which states that the most space-efficient way to pack spheres is in a pyramid shape...

, 1998)
Milnor conjecture
Milnor conjecture
In mathematics, the Milnor conjecture was a proposal by of a description of the Milnor K-theory of a general field F with characteristic different from 2, by means of the Galois cohomology of F with coefficients in Z/2Z. It was proved by .-Statement of the theorem:Let F be a field of...

(Vladimir Voevodsky
Vladimir Voevodsky
Vladimir Voevodsky is a Russian American mathematician. His work in developing a homotopy theory for algebraic varieties and formulating motivic cohomology led to the award of a Fields Medal in 2002.- Biography :...

, 1996)
Fermat's Last Theorem
Fermat's Last Theorem
In number theory, Fermat's Last Theorem states that no three positive integers a, b, and c can satisfy the equation an + bn = cn for any integer value of n greater than two....

(Andrew Wiles
Andrew Wiles
Sir Andrew John Wiles KBE FRS is a British mathematician and a Royal Society Research Professor at Oxford University, specializing in number theory...

and Richard Taylor
Richard Taylor (mathematician)
-External links:**...

, 1995)
Bieberbach conjecture
De Branges' theorem
In complex analysis, the Bieberbach conjecture or de Branges's theorem, posed by and proven by , states a necessary condition on a holomorphic function to map the open unit disk of the complex plane injectively to the complex plane....

(Louis de Branges
Louis de Branges de Bourcia
Louis de Branges de Bourcia is a French-American mathematician. He is the Edward C. Elliott Distinguished Professor of Mathematics at Purdue University in West Lafayette, Indiana. He is best known for proving the long-standing Bieberbach conjecture in 1984, now called de Branges' theorem...

, 1985)
Princess and monster game
Princess and monster game
In game theory, the princess and monster game is a pursuit-evasion game played by two players in a region. The game was devised by Rufus Isaacs and published in his book Differential Games as follows. "The monster searches for the princess, the time required being the payoff. They are both in a...

(Shmuel Gal
Shmuel Gal
Shmuel Gal is a professor of statistics at the University of Haifa in Israel.Gal received a Ph.D. in mathematics from the Hebrew University of Jerusalem....

, 1979)
Four color theorem
Four color theorem
In mathematics, the four color theorem, or the four color map theorem states that, given any separation of a plane into contiguous regions, producing a figure called a map, no more than four colors are required to color the regions of the map so that no two adjacent regions have the same color...

(Appel
Kenneth Appel
Kenneth Ira Appel is a mathematician who in 1976, with colleague Wolfgang Haken at the University of Illinois at Urbana-Champaign, solved one of the most famous problems in mathematics, the four-color theorem...

and Haken
Wolfgang Haken
Wolfgang Haken is a mathematician who specializes in topology, in particular 3-manifolds.In 1976 together with colleague Kenneth Appel at the University of Illinois at Urbana-Champaign, Haken solved one of the most famous problems in mathematics, the four-color theorem...

, 1977)

Millennium Prize Problems

Additive number theory

Number theory: prime numbers

General number theory

Algebraic number theory

Discrete geometry

Ramsey theory

General algebra

Combinatorics

Graph theory

Dynamics

Partial differential equations

Group theory

Set theory

Other

Problems solved recently

See also