Van der Waerden number
Encyclopedia
Van der Waerden's theorem states that for any positive integer
s r and k there exists a positive integer N such that if the integers {1, 2, ..., N} are colored
, each with one of r different colors, then there are at least k integers in arithmetic progression
all of the same color. The smallest such N is the van der Waerden number W(r,k).
There are two cases in which the van der Waerden number is easy to compute: first, W(1,k)=k for any integer k, since one color produces only trivial colorings RRRRR...RRR (for the single color denoted R). Second, W(r,2)=r+1, since we may construct a coloring that avoids arithmetic progressions of length 2 by using each color at most once, but once we use a color twice, a length 2 arithmetic progression is formed (e.g., for r=3, the longest coloring we can get that avoids an arithmetic progression of length 2 is RGB). There are only a few other van der Waerden numbers that are known exactly. Bounds in this table taken from Heule except where otherwise noted.
Van der Waerden numbers with r ≥ 2 are bounded by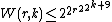
as proved by Timothy Gowers.
2-color van der Waerden numbers are bounded by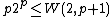
where p is prime, as proved by Berlekamp.
One sometimes also writes w(k1, k2, ..., kr) to mean the smallest number w such that any coloring of the integers { 1, 2, ..., w } with r colors contains a progression of length ki of color i, for some i. Such numbers are called off-diagonal van der Waerden numbers. Thus W(r, k) = w(k, k, ..., k) with r arguments. w(4, 3, 3) is known to be exactly 51.
Van der Waerden numbers are primitive recursive, as proved by Shelah; in fact he proved that they are (at most) on the fifth level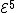
of the Grzegorczyk hierarchy
.
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s r and k there exists a positive integer N such that if the integers {1, 2, ..., N} are colored
Graph coloring
In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices share the...
, each with one of r different colors, then there are at least k integers in arithmetic progression
Arithmetic progression
In mathematics, an arithmetic progression or arithmetic sequence is a sequence of numbers such that the difference between the consecutive terms is constant...
all of the same color. The smallest such N is the van der Waerden number W(r,k).
There are two cases in which the van der Waerden number is easy to compute: first, W(1,k)=k for any integer k, since one color produces only trivial colorings RRRRR...RRR (for the single color denoted R). Second, W(r,2)=r+1, since we may construct a coloring that avoids arithmetic progressions of length 2 by using each color at most once, but once we use a color twice, a length 2 arithmetic progression is formed (e.g., for r=3, the longest coloring we can get that avoids an arithmetic progression of length 2 is RGB). There are only a few other van der Waerden numbers that are known exactly. Bounds in this table taken from Heule except where otherwise noted.
| r\k | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|
| 2 colors | 9 | 35 | 178 | 1,132 | > 3,703 | > 11,495 |
| 3 colors | 27 | > 292 | > 2,173 | > 11,191 | > 48,811 | > 238,400 |
| 4 colors | 76 | > 1,048 | > 17,705 | > 91,331 | > 420,217 | |
| 5 colors | > 170 | > 2,254 | > 98,740 | > 540,025 | ||
| 6 colors | > 223 | > 9,778 | > 98,748 | > 816,981 |
Van der Waerden numbers with r ≥ 2 are bounded by
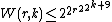
as proved by Timothy Gowers.
2-color van der Waerden numbers are bounded by
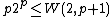
where p is prime, as proved by Berlekamp.
One sometimes also writes w(k1, k2, ..., kr) to mean the smallest number w such that any coloring of the integers { 1, 2, ..., w } with r colors contains a progression of length ki of color i, for some i. Such numbers are called off-diagonal van der Waerden numbers. Thus W(r, k) = w(k, k, ..., k) with r arguments. w(4, 3, 3) is known to be exactly 51.
Van der Waerden numbers are primitive recursive, as proved by Shelah; in fact he proved that they are (at most) on the fifth level
of the Grzegorczyk hierarchyGrzegorczyk hierarchy
The Grzegorczyk hierarchy , named after the Polish logician Andrzej Grzegorczyk, is a hierarchy of functions used in computability theory . Every function in the Grzegorczyk hierarchy is a primitive recursive function, and every primitive recursive function appears in the hierarchy at some level...
.