Road coloring conjecture
Encyclopedia
In graph theory
the road coloring theorem
, known until recently as the road coloring conjecture
, deals with synchronized
instructions. The issue involves whether by using such instructions, one can reach or locate an object or destination from any other point within a network (which might be a representation of city streets or a maze
). In the real world, this phenomenon would be as if you called a friend to ask for directions to his house, and he gave you a set of directions that worked no matter where you started from. This theorem also has implications in symbolic dynamics
.
The theorem was first conjectured by . It was proved by .
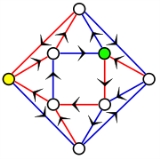
 The image to the right shows a directed graph
The image to the right shows a directed graph
on eight vertices
in which each vertex has out-degree 2. (Each vertex in this case also has in-degree 2, but that is not necessary for a synchronizing coloring to exist.) The edges of this graph have been colored red and blue to create a synchronizing coloring.
For example, consider the vertex marked in yellow. No matter where in the graph you start, if you traverse all nine edges in the walk "blue-red-red—blue-red-red—blue-red-red", you will end up at the yellow vertex. Similarly, if you traverse all nine edges in the walk "blue-blue-red—blue-blue-red—blue-blue-red", you will always end up at the vertex marked in green, no matter where you started.
The road coloring theorem states that for a certain category of directed graphs, it is always possible to create such a coloring.
where all the vertices have the same out-degree k. Let A be the alphabet containing the letters 1, ..., k. A synchronizing coloring (also known as a collapsible coloring) in G is a labeling of the edges in G with letters from A such that (1) each vertex has exactly one outgoing edge with a given label and (2) for every vertex v in the graph, there exists a word w over A such that all paths in G corresponding to w terminate at v.
The terminology synchronizing coloring is due to the relation between this notion and that of a synchronizing word
in finite automata theory.
For such a coloring to exist at all, it is necessary
that G be both strongly connected
and aperiodic. The road coloring theorem states that these two conditions are also sufficient
for such a coloring to exist. Therefore, the road coloring problem can be stated briefly as:
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
the road coloring theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
, known until recently as the road coloring conjecture
Conjecture
A conjecture is a proposition that is unproven but is thought to be true and has not been disproven. Karl Popper pioneered the use of the term "conjecture" in scientific philosophy. Conjecture is contrasted by hypothesis , which is a testable statement based on accepted grounds...
, deals with synchronized
Synchronization
Synchronization is timekeeping which requires the coordination of events to operate a system in unison. The familiar conductor of an orchestra serves to keep the orchestra in time....
instructions. The issue involves whether by using such instructions, one can reach or locate an object or destination from any other point within a network (which might be a representation of city streets or a maze
Maze
A maze is a tour puzzle in the form of a complex branching passage through which the solver must find a route. In everyday speech, both maze and labyrinth denote a complex and confusing series of pathways, but technically the maze is distinguished from the labyrinth, as the labyrinth has a single...
). In the real world, this phenomenon would be as if you called a friend to ask for directions to his house, and he gave you a set of directions that worked no matter where you started from. This theorem also has implications in symbolic dynamics
Symbolic dynamics
In mathematics, symbolic dynamics is the practice of modeling a topological or smooth dynamical system by a discrete space consisting of infinite sequences of abstract symbols, each of which corresponds to a state of the system, with the dynamics given by the shift operator...
.
The theorem was first conjectured by . It was proved by .
Example and intuition

Directed graph
A directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...
on eight vertices
Vertex (graph theory)
In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
in which each vertex has out-degree 2. (Each vertex in this case also has in-degree 2, but that is not necessary for a synchronizing coloring to exist.) The edges of this graph have been colored red and blue to create a synchronizing coloring.
For example, consider the vertex marked in yellow. No matter where in the graph you start, if you traverse all nine edges in the walk "blue-red-red—blue-red-red—blue-red-red", you will end up at the yellow vertex. Similarly, if you traverse all nine edges in the walk "blue-blue-red—blue-blue-red—blue-blue-red", you will always end up at the vertex marked in green, no matter where you started.
The road coloring theorem states that for a certain category of directed graphs, it is always possible to create such a coloring.
Mathematical description
Let G be a finite directed graphDirected graph
A directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...
where all the vertices have the same out-degree k. Let A be the alphabet containing the letters 1, ..., k. A synchronizing coloring (also known as a collapsible coloring) in G is a labeling of the edges in G with letters from A such that (1) each vertex has exactly one outgoing edge with a given label and (2) for every vertex v in the graph, there exists a word w over A such that all paths in G corresponding to w terminate at v.
The terminology synchronizing coloring is due to the relation between this notion and that of a synchronizing word
Synchronizing word
In computer science, more precisely, in the theory of deterministic finite automata , a synchronizing word or reset sequence is a word in the input alphabet of the DFA which sends any state of the DFA to one and the same state...
in finite automata theory.
For such a coloring to exist at all, it is necessary
Necessary and sufficient conditions
In logic, the words necessity and sufficiency refer to the implicational relationships between statements. The assertion that one statement is a necessary and sufficient condition of another means that the former statement is true if and only if the latter is true.-Definitions:A necessary condition...
that G be both strongly connected
Strongly connected component
A directed graph is called strongly connected if there is a path from each vertex in the graph to every other vertex. In particular, this means paths in each direction; a path from a to b and also a path from b to a....
and aperiodic. The road coloring theorem states that these two conditions are also sufficient
Necessary and sufficient conditions
In logic, the words necessity and sufficiency refer to the implicational relationships between statements. The assertion that one statement is a necessary and sufficient condition of another means that the former statement is true if and only if the latter is true.-Definitions:A necessary condition...
for such a coloring to exist. Therefore, the road coloring problem can be stated briefly as:
- Every finite strongly connected aperiodic directed graph of uniform out-degree has a synchronizing coloring.
Previous partial results
Previous partial or special-case results include the following:- If G is a finite strongly connected aperiodic directed graph with no multiple edgesMultiple edgesIn graph theory, multiple edges , are two or more edges that are incident to the same two vertices...
, and G contains a simple cycle of primePrime numberA prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
length which is a proper subset of G, then G has a synchronizing coloring. (O'Brien 1981)
- If G is a finite strongly connected aperiodic directed graph (multiple edges allowed) and every vertex has the same in-degree and out-degree k, then G has a synchronizing coloring. (Kari 2003)

